【数论学习】奇素数分解为两个数平方和

首先需要考虑哪些奇素数可能分解为两个数平方和。

引论：只有形如4k+1的奇素数可能被分解为两个数平方和。

证明：对于一个奇素数p能够被分解为两个数的平方和，这样a和b必定是一奇一偶，设a=2u、b=2v+1

代入原方程得：，令，则p=4k+1,得证。

接下来要考虑的是不是所有形如4k+1的素数都能够分解为两个素数和。

断言：形如4k+1的奇素数能够被分解为两个数平方和。

在证明这个断言前，需要说明一个等式：

只需要展开重新组合即可证明。

断言证明：

对于形如4k+1的p,则：

因此存在数A，使得，即而存在A,B使得成立，其中M>=1,如果M就为1时候，断言得证。

如果M>1时候，就需要尝试改变A,B的值使得等式依旧满足的情况下，M值变小，即满足,其中。

令u、v满足(u-A)%M=0、(v-B)%M=0，且u和v都属于(-M/2,M/2]：

，因此

,可以看出r<=1/2M

，其中(uA+vB)%M=(A^2+B^2)%M=0，说明(uA+vB)能够被M整除，自然uB-vA也能够被M整除

令，,则，其中r成立，断言得证。

因此一个奇素数p能够分解为两个数的平方和的充要条件是p能写出4k+1的形式；接下来进一步考虑求出a和b，使得。

求a和b:

可以看出断言的证明过程就是求解a、b的过程，第一步在于求解A，使得，该过程参见二次剩余方法求解

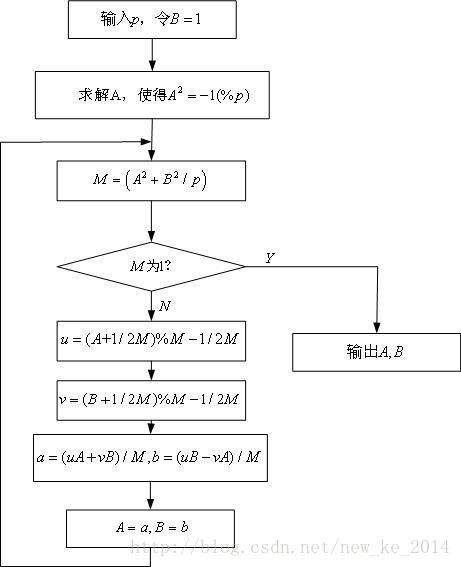
第二步，初始设置A和B(为1），求出a和b,a赋值给A,b赋值给B，迭代求解a、b，直到M为1，结束。整个个算法的流程图如下：

算法复杂度分析：

在(0，p)区间内，存在两个数，使得成立，且两个数之和为p；因此选取小的数使得，该数必然

则初始的M满足：。

求解过程，初始选择A情况下(M=(A^2+1)/p),算法的时间复杂度设为T(M)，

根据，每次都能够重新构造a和b,使得，且r<1/2M。

则T(M)<=T(M/2)+c，c表示计算一次a、b的时耗，因此T(M)<=clog(M);

整个求解的过程时耗T(M)<=clog(M)<=clog(p/4)=c/2logp.可以看出整个算法的时间复杂度不会超过O(logp);

代码实现：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

#define LL __int64

LL limit(LL a, LL M)//把a限定在[-M/2, M/2]范围内
{
	if (a > (M >> 1))
	{
		a -= M;
	}
	else if (a < -(M >> 1))
	{
		a += M;
	}

	return a;
}
LL prime_resolve(LL A, LL p)//(A^2+1)%p== 0
{
	LL M = (A * A + 1) / p;
	LL u,v;
	LL B = 1;
	LL a, b;
	while(M != 1)
	{
		u = A % M;
		v = B % M;
		v= limit(v, M);
		u= limit(u, M);
		a = (u * A + v * B) / M;
		b = (u * B - v * A) / M;
		A = a;
		B = b;
		M = (A * A + B * B) / p;
	}

	return A;
}

int main()
{
	LL A, p;
	scanf("%I64d %I64d", &A, &p);//假设初始的A已知
	A = prime_resolve(A, p);
	LL B = sqrt(p - (A * A));
	printf("%I64d^2+%I64d^2=%I64d\n", A, B, p);
	return 0;
}