Jaihk662
Jaihk662

Codeforces Round #202 (Div. 1): D. Turtles（Lindström–Gessel–Viennot lemma定理+DP）

Codeforces Round #202 (Div. 1): D. Turtles（Lindström–Gessel–Viennot lemma定理+DP）_第1张图片

 

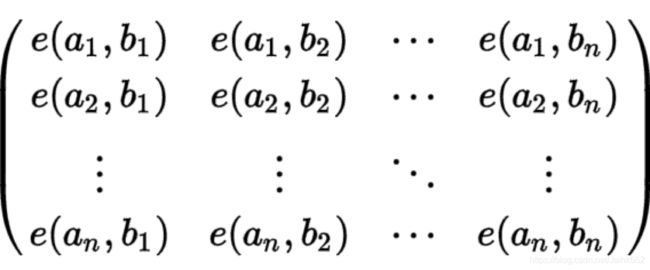
题意：

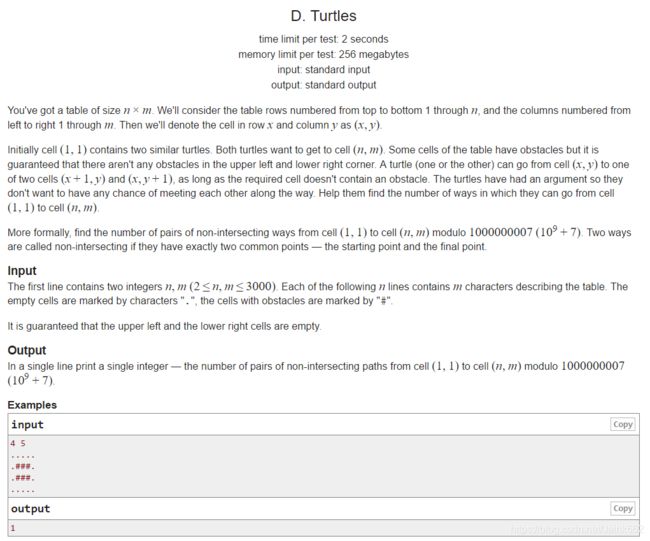
给你一个n*m的地图，"#"是障碍，"."是路，不能走出边界，问从(1,1)到(n,m)选出两条不相交最短路径的方案数是多少（其中起点和终点相同不算相交）

 

思路：

知道Lindström–Gessel–Viennot lemma定理就是水题了

对于一个无边权有向无环图，给出n个起点和对应的n个终点，这n条不相交路径的方案数为

行列式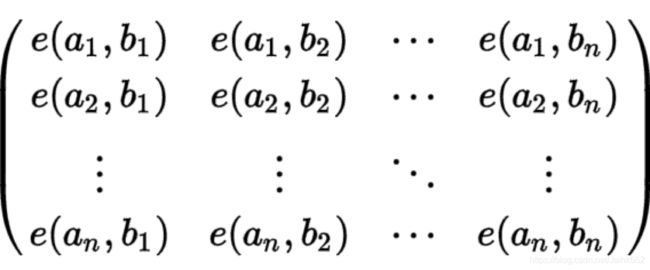Codeforces Round #202 (Div. 1): D. Turtles（Lindström–Gessel–Viennot lemma定理+DP）_第2张图片的值

其中e(a, b)为图上a点到b点的方案个数

 

对于这题

行列式大小为2

且a1 = (1, 2)；a2 = (2, 1)；b1 = (n-1, m)；b2 = (n, m-1)；

直接套就可以了

 

#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define LL long long
#define mod 1000000007
char str[3005][3005];
int dp1[3005][3005], dp2[3005][3005];
int main(void)
{
	int n, m, i, j;
	scanf("%d%d", &n, &m);
	for(i=1;i<=n;i++)
		scanf("%s", str[i]+1);
	if(str[1][2]=='#' || str[2][1]=='#')
		printf("0\n");
	else
	{
		dp1[1][2] = dp2[2][1] = 1;
		for(i=1;i<=n;i++)
		{
			for(j=1;j<=m;j++)
			{
				if(i+j<=3 || str[i][j]!='.')
					continue;
				dp1[i][j] = (dp1[i][j-1]+dp1[i-1][j])%mod;
				dp2[i][j] = (dp2[i][j-1]+dp2[i-1][j])%mod;
			}
		}
		//printf("%d %d %d %d\n", dp1[n-1][m], dp1[n][m-1], dp2[n-1][m], dp2[n][m-1]);
		printf("%lld\n", (((LL)dp1[n-1][m]*dp2[n][m-1]-(LL)dp1[n][m-1]*dp2[n-1][m])%mod+mod)%mod);
	}
	return 0;
}

 

你可能感兴趣的:(#,数论)

  • 致良知之寄诸用明书 BonSun
    众所周知，当今社会，父母和社会、学校对学生的期望往往是唯分数论，包括每个人对成功的理解也往往是功名利禄，忽视了最基本的学问。文中提到，花之千叶者无实，为其华美太发露耳。人只有沉下心来，韬光养晦，才能拥有真正的学问和本领。
  • Python【math数学函数】 Alan_Lowe #Pythonpython
    Python【math数学函数】文章目录Python【math数学函数】数论与表示函数1.ceil()和floor()2.comb()3.copysign()4.fabs()5.factorial()6.gcd()7.lcm()幂函数与对数函数1.exp()和math.e和pow()2.log()和log2()和log10()3.sqrt(x)三角函数1.asin、acos()、atan()2.s
  • python 实现eulers totient欧拉方程算法 luthane 算法python开发语言
    eulerstotient欧拉方程算法介绍欧拉函数（Euler’sTotientFunction），通常表示为()，是一个与正整数相关的函数，它表示小于或等于的正整数中与互质的数的数目。欧拉函数在数论和密码学中有广泛的应用。欧拉函数的性质1.**对于质数，有φ(p)=p−1∗∗φ(p)=p−1^{**}φ(p)=p−1∗∗。2.**如果是质数的次幂，即n=pkn=p^kn=pk，则φ(n)=pk−
  • 算法设计与分析学习（6）——数论 罗塞菈桔梨萝柚 算法学习算法线性代数
    数论整除基本概念若aaa和bbb为整数，且a≠0a≠0a=0若存在整数qqq使得b=aqb=aqb=aq，那么就说aaa可以整除bbb或是bbb被aaa整除，记作a∣ba|ba∣b。aaa也被称为bbb的约数，bbb也被称为a的倍数。若bbb不能被aaa整除，则记作a∤ba\not{|}ba∣b。整数p≠0,±1p≠0,±1p=0,±1，且除了±1,±p±1,±p±1,±p外没有其他的约数
  • 数论——欧几里得算法 NarutoTime 数论算法c++数据结构c语言
    1.欧几里得简介    欧几里得（希腊文：Ευκλειδης，约公元前330年—公元前275年），古希腊数学家，被称为“几何之父”。他最著名的著作《几何原本》是欧洲数学的基础，在书中他提出五大公设。欧几里得的《几何原本》被广泛的认为是历史上最成功的教科书。欧几里得也写了一些关于透视、圆锥曲线、球面几何学及数论的作品。2.欧几里得算法欧几里得算法用于：求解a和b的最大公约数。最大公约数英文为：Gre
  • 数论——扩展欧几里得算法 NOI_yzk
    欧几里得&拓展欧几里得（Euclid&Extend-Euclid）欧几里得算法（Euclid）背景：欧几里德算法又称辗转相除法，用于计算两个正整数a，b的最大公约数。——百度百科代码：递推的代码是相当的简洁：intgcd(inta,intb){returnb==0?a:gcd(b,a%b);}分析：方法说了是辗转相除法，自然没有什么好介绍的了。。Fresh肯定会觉得这样递归下去会不会爆栈？实际上在
  • 数论学习1（欧几里德算法+唯一分解定理+埃氏筛+拓展欧几里德+同余与模算术） new出新对象！ 数学数算法学习
    目录1.唯一分解定理2.欧几里德算法（求最大公约数）3.求最小公倍数4.埃氏筛5.拓展欧几里德算法(1)证明一下线性方程组的正数的最小值是多少，(2)如何通过裴蜀定理退出拓展欧几里得算法(贝祖定理)6.同余与模算术(1)取模运算操作加法取模运算减法取模运算乘法取模运算(2)特殊的取模操作大整数取模幂取模(3)同余式，乘法逆元，费马小定理今天也是小小的开始学习数论方面的知识了，首先数论的入门章节必然
  • Collatz 猜想和 Python 不连续小姐
    PythonDay4:CollatzConjecture原来总有学生问我，微积分有什么用啊，我说如果微积分学好了，也许抽象代数和数论就能学好，那最后就能像AndrewWiles一样上人物年度杂志的封面了.(AndrewWiles证明了Fermat'sLastTheorem，费玛大定理).[captionid="attachment_1466"align="alignnone"width="300"
  • 初等数论--整除--带余除法 WeidanJi 初等数论数学密码学信息安全
    初等数论--整除--带余除法概念基本性质带余除法博主本人是初学初等数论（整除+同余+原根），本意是想整理一些较难理解的定理、算法，加深记忆也方便日后查找；如果有错，欢迎指正。我整理成一个系列：初等数论，方便检索。概念初等数论研究对象是整数集合和自然数集合。初等数论研究对象是整数集合和自然数集合。初等数论研究对象是整数集合和自然数集合。b∣a:若a,b∈Z,b≠0，∃c∈Z,使a=bc,则称b整除a
  • 河南萌新2024第四场 Pown_ShanYu 算法数据结构
    C岗位分配题目大意：有n个岗位，m位志愿者，每个岗位至少需要a个志愿者，并且可以有志愿者可以空闲下来作预备，给出可能的分配情况总数思路：首先将每个岗位分配好至少需要的志愿者，再将剩下的人进行分配，那就满足球同盒不同模型（允许空盒），可用隔板法进行分配，需要额外开设一个空闲岗位用来预备，那么按照4个人去4个岗位，那么为c73，具体操作可看数论模板中发布的隔板法问题，递归求组合数Solved：intn
  • 【读书笔记】吴非《致青年教师》(4) 冬儿菇凉
    一、精要摘录(48——106页)1.教育教学不能“唯分数论“，比分数重要的是学生思维品质和解决实际问题的能力。2.一名教师心中有使命感，心中有学生才会很在意学生对他的态度，在意学生的接受度。3.作为教师，你要善于向学生问出有意思的问题。4.教育就是要培养好习惯，教是为了达到不需要教学生，不需要老师教了是教学的成功，也是教师的职业追求。5.教师是学习者，在学习上教师首先要郑重其事，学生才有可能养成敬
  • 【代码随想录算法训练营Day39】62.不同路径；63. 不同路径 II 想做一只潜水的猪 算法
    文章目录❇️Day39第九章动态规划part02✴️今日任务❇️62.不同路径自己的思路自己的代码随想录思路随想录代码❇️63.不同路径II自己的思路自己的代码随想录代码❇️Day39第九章动态规划part02✴️今日任务今天开始逐渐有dp的感觉了，题目不多，就两个不同路径，可以好好研究一下62.不同路径63.不同路径II❇️62.不同路径本题大家掌握动态规划的方法就可以。数论方法有点非主流，很难
  • 算法D39 | 动态规划2 | 62.不同路径 63. 不同路径 II memolaner 算法训练营算法动态规划数据结构c++python
    今天开始逐渐有dp的感觉了，题目不多，就两个不同路径，可以好好研究一下62.不同路径本题大家掌握动态规划的方法就可以。数论方法有点非主流，很难想到。代码随想录视频讲解：动态规划中如何初始化很重要！|LeetCode：62.不同路径_哔哩哔哩_bilibili这个题看到路径的表示，第一直觉就是一个组合数的问题，学了一下C++计算组合数防止溢出的小技巧。第二个方法再动态规划完成，重点是把二维的动态规划
  • 牛客周赛 Round 35（A,B,C,D,E,F,G） 邪神与厨二病 牛客算法暴力c++数论滑动窗口单调队列贪心构造
    这场简单，甚至赛时90分钟不到就AK了。比赛链接，队友题解友链刚入住学校监狱，很不适应，最近难受的要死，加上最近几场CF打的都不顺利，san值要爆掉了，只能慢慢补题了。这场C是个滑动窗口，D是贪心，E是有点麻烦的构造，FG是数论。A小红的字符串切割思路：记录一下字符串长度，然后从中间拆开。code：#include#include#includeusingnamespacestd;strings;
  • 算法——数论——同余 戏拈秃笔 数据结构与算法（java版）算法
    目录同余一、试题算法训练同余方程同余同余使人们能够用等式的形式简洁地描述整除关系同余：若m（正整数），a和b是整数，a%m==b%m，或(a-b)%m==0，记为ab(modm)求解一元线性同余方程等价于求解二元线性丢番图方程一元线性同余方程，解法看下面第一题二元线性丢番图方程逆：的一个解为a模m的逆一、试题算法训练同余方程问题描述求关于x的同余方程ax≡1(modb)的最小正整数解。输入格式输入
  • pku acm 题目分类 moxiaomomo 算法数据结构numbers优化calendarcombinations
    1.搜索//回溯2.DP（动态规划）3.贪心北大ACM题分类2009-01-2714.图论//Dijkstra、最小生成树、网络流5.数论//解模线性方程6.计算几何//凸壳、同等安置矩形的并的面积与周长sp;7.组合数学//Polya定理8.模拟9.数据结构//并查集、堆sp;10.博弈论1、排序sp;1423,1694,1723,1727,1763,1788,1828,1838,1840,22
  • C++STL之Queue容器 芯片烧毁大师 数据结构C++c++开发语言
    C++STL之Queue容器1.再谈队列回顾一下之前所学的队列，队列和栈不同，队列是一种先进先出的数据结构，STL的队列内容极其重要，虽然内容较少但是请务必掌握，STL的队列是快速构建搜索算法以及相关的数论图论的状态存储的基础。2.相关头文件头文件：#include3.初始化格式为：**explicit**queue(**const**container_type&ctnr=container_t
  • 数字签名算法MD5withRSA Just_Paranoid 技术流Clipmd5rsasignatrue
    数字签名MD5withRSA，：将正文通过MD5数字摘要后，将密文再次通过生成的RSA密钥加密，生成数字签名，将明文与密文以及公钥发送给对方，对方拿到私钥/公钥对数字签名进行解密，然后解密后的，与明文经过MD5加密进行比较，如果一致则通过使用Signature的API来实现MD5withRSARSA原理：RSA算法基于一个十分简单的数论事实，将两个大素数相乘十分容易，但反过来想要对其乘积进行因式分
  • 2301: 不定方程解的个数 jht0105 算法
    题目描述输出不定方程解的个数。在数学中，不定方程是数论中的一个重要课题，在各种比赛中也常常出现.对于不定方程，有时我们往往只求非负整数解，现有方程ax+by+c=0，其中x、y为未知量且不超过10000，当给定a、b、c的值以后，可求出n组x、y的非负整数解，n>=0，,其中a，b，c均为[-10000,10000].输入描述一行，三个空格隔开的整数，为a、b、c的值。输出描述一个整数，为合法的解
  • python伯努利多项式 微小冷 #sympypython开发语言sympy伯努利数排列组合符号计算
    文章目录伯努利数和多项式sympy实现伯努利数是一种在数学、物理和工程中广泛应用的特殊数列，以瑞士数学家雅各布·伯努利（JacobBernoulli）的名字命名，并在许多领域中发挥重要作用。在数学中，它们与斐波那契数列、卡塔兰数、贝尔数等数列有密切联系，可以用于解决循环问题、组合问题和递推关系等数学问题。伯努利数和多项式伯努利(Bernoulli)数是一组在数论和复分析中出现的数，与伯努利多项式有
  • 二次剩余问题x的求解及代码实现（python） JustGo12 数论安全1024程序员节
    一、问题引入二次剩余是数论基本概念之一。它是初等数论中非常重要的结果，不仅可用来判断二次同余式是否有解，还有很多用途。C.F.高斯称它为算术中的宝石，他一人先后给出多个证明。[1]研究二次剩余的理论称为二次剩余理论。二次剩余理论在实际上有广泛的应用，包括从噪音工程学到密码学以及大数分解。即关于方x^2≡a(modp)对于这个方程，求出满足条件的x。二、x的求解在上述问题下，根据p值的不同性质，可以
  • 【数论】exgcd 扩展欧几里得算法 Texcavator 数论算法
    参考：exgcd详解-zzt1208-博客园(cnblogs.com)exgcd（扩展欧几里得算法），用来求形如ax+by=gcd(a,b)ax+by=gcd(a,b)ax+by=gcd(a,b)（a,ba,ba,b为常数）的方程的一组整数解。（如果不确定等号右边是不是gcd，可以先当做gcd，求出来之后验证，是的话就是解，不是的话就不是解）推导见上面的链接，这篇只放个板子codeintexgcd
  • 2021-07-30 RX-0493
    学了一会数论，好难1.乘法逆元：a/b%p,若a/b在进行取模运算时，会出现精度问题，而且模运算对除法不适用，（没有分配律，大概就这意思）而求出乘法逆元后，可以把原式变为a*x%p的形式，且值不变。a*x≡1（modp）中，a,p为已知量，则x为a的乘法逆元。例题：乘法逆元设p=k*i+r,(1usingnamespacestd;constintN=20000530;intn,p,inv[N];i
  • 同余数论性质 clmm_ 算法
    同余概念当a%m==b%m，说明a和b同余，写作若a≡b(modm)性质衍生出几条性质1.m|abs(a-b)，即|a-b|是m的倍数。（注意，0是任何数的倍数）2.当a≡b(modm)，c≡d(modm)，有ac≡bd(modm)有a+c≡b+d(modm)有a-c≡b-d(modm)证明如下
  • 读《爱心与教育》第八天 皮_小皮
    作为一名教师，尤其是班主任老师，“培优转差”是教育工作的一项重要内容，读了李镇西老师的《爱心与教育》，自己受到不小的启发，对“优生”的培养和后进生的转化有了新的认识和思考。对“优生”的重新认识——李老师说：“优生”当然应该是指品学兼优的学生，但在现在不少教师、家长的眼中，所谓“优生”更多的是指学习成绩拔尖的学生（即尖子生）。的确，在升学竞争和应试教育的大环境下，很多教育者都以分数论英雄，对“优生”
  • RSA算法 superdont 图像加密算法java服务器
    RSA算法是一个非对称加密算法，它依赖于数论中的大整数因数分解问题的困难性。在RSA中，加密和解密使用不同的密钥，分别称为公钥和私钥。RSA算法的基本原理包括以下几个步骤：密钥生成：a.选择两个大的质数(p)和(q)。b.计算它们的乘积(n=pq)，n的长度就是密钥长度。c.计算欧拉函数(\phi(n)=(p-1)(q-1))。d.选择一个整数(e)，使得(1
  • 日精进110天 金八力韩英雪
    敬爱的老师，智慧的班主任，亲爱的跃友们：大家好！我是来自山峰教外教育的韩英雪，今天是我的日精进行动第110天，给大家分享我今天的进步，我们互相勉励，携手前行。每天进步一点点，距离成功便不远。1、比学习:个体身心发展的规律。顺序性，阶段性，不平衡性，互补性，个别差异性和整体性。个体身心发展的能动动因主要由内发论，外数论多因素互相作用论。其中内发论的代表人物包括孟子，弗洛伊德，威尔逊，格赛尔，霍尔等外
  • [C语言]Day04作业：输出菱形,判断水仙花数,输出a = aaaaa MrDorli C语言学习c语言
    /*1.在屏幕上输出以下图案：*************************************************************************************2.求出0～999之间的所有“水仙花数”并输出。“水仙花数”是指一个三位数，其各位数字的立方和确好等于该数本身，如；153＝1＋5＋3?，则153是一个“水仙花数”。在数论中，水仙花数（Narciss
  • 信安数基2-同余方程 利賀田
    基本概念及一次同余式同余式是数论的基本概念之一，设m是给定的一个正整数，a、b是整数，若满足m|(a-b)，则称a与b对模m同余，记为a≡b(modm)，或记为a≡b(m)。这个式子称为模m的同余式，若m∤(a-b)，则称a、b对模m不同余，同余概念又常表达为：1.a=b+km(k∈Z)；2.a和b被m除时有相同的[余数]。同余式的记号由高斯(Gauss,C.F.)于1800年首创,发表在他的数论
  • 【数论】矩阵快速幂 Texcavator 数论矩阵算法数据结构
    参考：P3193[HNOI2008]GT考试题解放个板子structMartix{inta[30][30];//在这里修改矩阵的大小Martix(){memset(a,0,sizeof(a));}Martixoperator*(constMartix&B)const//乘法运算符重载{Martixres;for(inti=0;i>=1;a=a*a;}returnans;}
  • Hadoop(一) 朱辉辉33 hadooplinux
    今天在诺基亚第一天开始培训大数据，因为之前没接触过Linux，所以这次一起学了，任务量还是蛮大的。 首先下载安装了Xshell软件，然后公司给了账号密码连接上了河南郑州那边的服务器，接下来开始按照给的资料学习，全英文的，头也不讲解，说锻炼我们的学习能力，然后就开始跌跌撞撞的自学。这里写部分已经运行成功的代码吧.    在hdfs下，运行hadoop fs -mkdir /u
  • maven An error occurred while filtering resources blackproof maven报错
    转：http://stackoverflow.com/questions/18145774/eclipse-an-error-occurred-while-filtering-resources   maven报错： maven An error occurred while filtering resources   Maven -> Update Proje
  • jdk常用故障排查命令 daysinsun jvm
    linux下常见定位命令： 1、jps      输出Java进程       -q       只输出进程ID的名称，省略主类的名称；       -m      输出进程启动时传递给main函数的参数；     &nb
  • java 位移运算与乘法运算 周凡杨 java位移运算乘法
      对于 JAVA 编程中，适当的采用位移运算，会减少代码的运行时间，提高项目的运行效率。这个可以从一道面试题说起：     问题： 用最有效率的方法算出2 乘以8 等於几?” 答案：2 << 3 由此就引发了我的思考，为什么位移运算会比乘法运算更快呢？其实简单的想想，计算机的内存是用由 0 和 1 组成的二
  • java中的枚举(enmu) g21121 java
    从jdk1.5开始，java增加了enum(枚举)这个类型，但是大家在平时运用中还是比较少用到枚举的，而且很多人和我一样对枚举一知半解，下面就跟大家一起学习下enmu枚举。先看一个最简单的枚举类型，一个返回类型的枚举： public enum ResultType { /** * 成功 */ SUCCESS, /** * 失败 */ FAIL,
  • MQ初级学习 510888780 activemq
    1.下载ActiveMQ 去官方网站下载：http://activemq.apache.org/ 2.运行ActiveMQ 解压缩apache-activemq-5.9.0-bin.zip到C盘，然后双击apache-activemq-5.9.0-\bin\activemq-admin.bat运行ActiveMQ程序。 启动ActiveMQ以后，登陆：http://localhos
  • Spring_Transactional_Propagation 布衣凌宇 springtransactional
    //事务传播属性 @Transactional(propagation=Propagation.REQUIRED)//如果有事务，那么加入事务，没有的话新创建一个 @Transactional(propagation=Propagation.NOT_SUPPORTED)//这个方法不开启事务 @Transactional(propagation=Propagation.REQUIREDS_N
  • 我的spring学习笔记12-idref与ref的区别 aijuans spring
    idref用来将容器内其他bean的id传给<constructor-arg>/<property>元素，同时提供错误验证功能。例如： <bean id ="theTargetBean" class="..." /> <bean id ="theClientBean" class=&quo
  • Jqplot之折线图 antlove jsjqueryWebtimeseriesjqplot
    timeseriesChart.html <script type="text/javascript" src="jslib/jquery.min.js"></script> <script type="text/javascript" src="jslib/excanvas.min.js&
  • JDBC中事务处理应用 百合不是茶 javaJDBC编程事务控制语句
      解释事务的概念; 事务控制是sql语句中的核心之一;事务控制的作用就是保证数据的正常执行与异常之后可以恢复   事务常用命令:             Commit提交         
  • [转]ConcurrentHashMap Collections.synchronizedMap和Hashtable讨论 bijian1013 java多线程线程安全HashMap
    在Java类库中出现的第一个关联的集合类是Hashtable，它是JDK1.0的一部分。 Hashtable提供了一种易于使用的、线程安全的、关联的map功能，这当然也是方便的。然而，线程安全性是凭代价换来的――Hashtable的所有方法都是同步的。此时，无竞争的同步会导致可观的性能代价。Hashtable的后继者HashMap是作为JDK1.2中的集合框架的一部分出现的，它通过提供一个不同步的
  • ng-if与ng-show、ng-hide指令的区别和注意事项 bijian1013 JavaScriptAngularJS
            angularJS中的ng-show、ng-hide、ng-if指令都可以用来控制dom元素的显示或隐藏。ng-show和ng-hide根据所给表达式的值来显示或隐藏HTML元素。当赋值给ng-show指令的值为false时元素会被隐藏，值为true时元素会显示。ng-hide功能类似，使用方式相反。元素的显示或
  • 【持久化框架MyBatis3七】MyBatis3定义typeHandler bit1129 TypeHandler
    什么是typeHandler? typeHandler用于将某个类型的数据映射到表的某一列上，以完成MyBatis列跟某个属性的映射   内置typeHandler MyBatis内置了很多typeHandler，这写typeHandler通过org.apache.ibatis.type.TypeHandlerRegistry进行注册，比如对于日期型数据的typeHandler，
  • 上传下载文件rz,sz命令 bitcarter linux命令rz
    刚开始使用rz上传和sz下载命令： 因为我们是通过secureCRT终端工具进行使用的所以会有上传下载这样的需求： 我遇到的问题： sz下载A文件10M左右，没有问题 但是将这个文件A再传到另一天服务器上时就出现传不上去，甚至出现乱码，死掉现象，具体问题 解决方法： 上传命令改为;rz -ybe 下载命令改为：sz -be filename 如果还是有问题： 那就是文
  • 通过ngx-lua来统计nginx上的虚拟主机性能数据 ronin47 ngx-lua　统计 解禁ip
    介绍 以前我们为nginx做统计,都是通过对日志的分析来完成.比较麻烦,现在基于ngx_lua插件,开发了实时统计站点状态的脚本,解放生产力.项目主页: https://github.com/skyeydemon/ngx-lua-stats 功能 支持分不同虚拟主机统计, 同一个虚拟主机下可以分不同的location统计. 可以统计与query-times request-time
  • java-68-把数组排成最小的数。一个正整数数组，将它们连接起来排成一个数，输出能排出的所有数字中最小的。例如输入数组{32, 321}，则输出32132 bylijinnan java
    import java.util.Arrays; import java.util.Comparator; public class MinNumFromIntArray { /** * Q68输入一个正整数数组，将它们连接起来排成一个数，输出能排出的所有数字中最小的一个。 * 例如输入数组{32, 321}，则输出这两个能排成的最小数字32132。请给出解决问题
  • Oracle基本操作 ccii Oracle SQL总结Oracle SQL语法Oracle基本操作Oracle SQL
    一、表操作 1. 常用数据类型 NUMBER(p,s)：可变长度的数字。p表示整数加小数的最大位数，s为最大小数位数。支持最大精度为38位 NVARCHAR2(size)：变长字符串，最大长度为4000字节（以字符数为单位） VARCHAR2(size)：变长字符串，最大长度为4000字节（以字节数为单位） CHAR(size)：定长字符串，最大长度为2000字节，最小为1字节，默认
  • [强人工智能]实现强人工智能的路线图 comsci 人工智能
        1：创建一个用于记录拓扑网络连接的矩阵数据表      2:自动构造或者人工复制一个包含10万个连接(1000*1000)的流程图      3：将这个流程图导入到矩阵数据表中      4：在矩阵的每个有意义的节点中嵌入一段简单的
  • 给Tomcat，Apache配置gzip压缩(HTTP压缩)功能 cwqcwqmax9 apache
    背景： HTTP 压缩可以大大提高浏览网站的速度，它的原理是，在客户端请求网页后，从服务器端将网页文件压缩，再下载到客户端，由客户端的浏览器负责解压缩并浏览。相对于普通的浏览过程HTML ,CSS,Javascript , Text ，它可以节省40%左右的流量。更为重要的是，它可以对动态生成的，包括CGI、PHP , JSP , ASP , Servlet,SHTML等输出的网页也能进行压缩，
  • SpringMVC and Struts2 dashuaifu struts2springMVC
    SpringMVC VS Struts2 1: spring3开发效率高于struts 2: spring3 mvc可以认为已经100%零配置 3: struts2是类级别的拦截， 一个类对应一个request上下文， springmvc是方法级别的拦截，一个方法对应一个request上下文，而方法同时又跟一个url对应 所以说从架构本身上 spring3 mvc就容易实现r
  • windows常用命令行命令 dcj3sjt126com windowscmdcommand
    在windows系统中，点击开始－运行，可以直接输入命令行，快速打开一些原本需要多次点击图标才能打开的界面，如常用的输入cmd打开dos命令行，输入taskmgr打开任务管理器。此处列出了网上搜集到的一些常用命令。winver 检查windows版本 wmimgmt.msc 打开windows管理体系结构(wmi) wupdmgr windows更新程序 wscrip
  • 再看知名应用背后的第三方开源项目 dcj3sjt126com ios
    知名应用程序的设计和技术一直都是开发者需要学习的，同样这些应用所使用的开源框架也是不可忽视的一部分。此前《 iOS第三方开源库的吐槽和备忘》中作者ibireme列举了国内多款知名应用所使用的开源框架，并对其中一些框架进行了分析，同样国外开发者 @iOSCowboy也在博客中给我们列出了国外多款知名应用使用的开源框架。另外txx's blog中详细介绍了 Facebook Paper使用的第三
  • Objective-c单例模式的正确写法 jsntghf 单例iosiPhone
    一般情况下，可能我们写的单例模式是这样的： #import <Foundation/Foundation.h> @interface Downloader : NSObject + (instancetype)sharedDownloader; @end #import "Downloader.h" @implementation
  • jquery easyui datagrid 加载成功，选中某一行 hae jqueryeasyuidatagrid数据加载
    1.首先你需要设置datagrid的onLoadSuccess $( '#dg' ).datagrid({onLoadSuccess :  function (data){      $( '#dg' ).datagrid( 'selectRow' ,3); }});   2.onL
  • jQuery用户数字打分评价效果 ini JavaScripthtmljqueryWebcss
    效果体验：http://hovertree.com/texiao/jquery/5.htmHTML文件代码： <!DOCTYPE html> <html xmlns="http://www.w3.org/1999/xhtml"> <head> <title>jQuery用户数字打分评分代码 - HoverTree</
  • mybatis的paramType kerryg DAOsql
    MyBatis传多个参数： 1、采用#{0},#{1}获得参数：    Dao层函数方法：     public User selectUser(String name,String area); 对应的Mapper.xml    <select id="selectUser" result
  • centos 7安装mysql5.5 MrLee23 centos
    首先centos7 已经不支持mysql，因为收费了你懂得，所以内部集成了mariadb，而安装mysql的话会和mariadb的文件冲突，所以需要先卸载掉mariadb，以下为卸载mariadb，安装mysql的步骤。   #列出所有被安装的rpm package rpm -qa | grep mariadb   #卸载 rpm -e mariadb-libs-5.
  • 利用thrift来实现消息群发 qifeifei thrift
               Thrift项目一般用来做内部项目接偶用的，还有能跨不同语言的功能，非常方便，一般前端系统和后台server线上都是3个节点，然后前端通过获取client来访问后台server，那么如果是多太server，就是有一个负载均衡的方法，然后最后访问其中一个节点。那么换个思路，能不能发送给所有节点的server呢，如果能就
  • 实现一个sizeof获取Java对象大小 teasp javaHotSpot内存对象大小sizeof
       由于Java的设计者不想让程序员管理和了解内存的使用，我们想要知道一个对象在内存中的大小变得比较困难了。本文提供了可以获取对象的大小的方法，但是由于各个虚拟机在内存使用上可能存在不同，因此该方法不能在各虚拟机上都适用，而是仅在hotspot 32位虚拟机上，或者其它内存管理方式与hotspot 32位虚拟机相同的虚拟机上 适用。     
  • SVN错误及处理 xiangqian0505 SVN提交文件时服务器强行关闭
    在SVN服务控制台打开资源库“SVN无法读取current” ---摘自网络 写道 SVN无法读取current修复方法 Can't read file : End of file found 文件：repository/db/txn_current、repository/db/current   其中current记录当前最新版本号，txn_current记录版本库中版本
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他