牛客练习赛 53 ABC 题解

A

题目描述
超越学姐非常喜欢自己的名字，以至于英文字母她只喜欢“c”和“y”。因此超越学姐喜欢只含有“c”和“y”的字符串，且字符串中不能出现两个连续的“c”。请你求出有多少种长度为n的字符串是超越学姐喜欢的字符串。答案对1e9+7取模。
输入描述:
输入一个整数n。
1<=n<=100000
输出描述:
输出一个整数表示答案。
示例1
输入
复制
3
输出
复制
5
说明
cyy,cyc,yyy,yyc,ycy

思路：你可以举一些例子试试，然后会发现规律是斐波那契

#include 
#include 
#define ll long long
using namespace std;
const int maxn=3000005,mod=1000000007;
ll v[maxn];
int main()
{
    int n;
    scanf("%d",&n);
    v[1]=2,v[2]=3;
    for(int a=3;a<=n;a++)
    {
        v[a]=(v[a-1]+v[a-2])%mod;
    }
    printf("%lld\n",v[n]);
    return 0;
}

B

由于n越大jelly越美味，这里n<=3000000,只需求这个式子对1e9+7取模的值。
输入描述:
第一行输入一个整数 n。 1<=n<=3000000。
输出描述:
输出一个整数表示答案。
示例1
输入
复制
3
输出
复制
22

思路：先进行转化

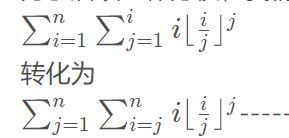
转化的好处就是在计算下面这个东西

的时候幂的次数j在本次求和中是不会发生变化的，而且在外层中j是递增的，比如当 j=1的时候你求的是1¹ ,2¹ ,3¹…(n/1)¹ ,当j=2时，就求的是 1²,2²,3²…(n/2)²,所以你每次就不用算快速幂了，直接乘一次就行了，因为它的幂数是递增的
然后还有一个小知识点就是 x,x+1,x+2,x+3,…,y 这个序列的和就是（x+y）*（y-x+1)/2

#include 
#include 
#define ll long long
using namespace std;
const int maxn=3000005,mod=1000000007;
ll v[maxn];
ll summ(ll x,ll y)
{
    return (x+y)*(y-x+1)/2%mod;
}
int main()
{
    int n;
    scanf("%d",&n);
    ll ans=0;
    for(int a=1;a<=n;a++)
    {
        v[a]=1;
    }
    for(int j=1;j<=n;j++)
    {
        for(int i=j;i<=n;i+=j) 
        {
            v[i/j]=(v[i/j]*(i/j))%mod;
            ans+=summ(i,min(j+i-1,n))*v[i/j];
            ans=ans%mod;
        }
    }
    printf("%lld\n",ans);
    return 0;
}

可能你对上面的for循环里面的东西不是太懂，我再解释一下，比如当j=3的时候，v[1]表示的就是当i/j为1，那么i可以是3，4，5,因为此时i*[i/j]^j 只有i是在变化的，你只需要计算（3+4+5）*[i/j]^j 就行了，而此时v[i/j]的值就是[i/j]^j

C

有n个长度为m的文本串，每个串只含有’0’和’1’。接下来有Q次询问，每次给出一个长度为m的字符串，且只含有’0’,‘1’和’’。如10_1_1。下划线可以匹配’0’或’1’。即10_1_1可以匹配101111,101101,100111,100101四种串。每次询问求出n个文本串中有多少个可以与当前询问的串匹配。
输入描述:
第一行输入n,m
接下来n行，每行输入一个长度为m的01串表示一个文本串。
第n+2行输入Q
接下来Q行，每行输入一个长度为m的字符串(只包含’0’,‘1’,’’)。
1<=n,m<=1000,1<=Q<=3000。
输出描述:
对于每次询问，输出n个文本串中有多少个与当前询问的串匹配。
示例1
输入
复制
5 6
101101
011011
100110
111000
101111
2
1011_1
1__1__
输出
复制
2
3
说明
第一次询问：有101101，101111与1011_1匹配
第二次询问：有101101, 100110, 101111与1__1__匹配

思路：这个题用到了 bitset 的知识，以前没学过这个东西，然后学了一下，发现这个东西比较特殊的一点就是比如你定义了两个数组v[100],s[100]这两个数组是不能 整个进行 | & 之类的运算，只能分成单个的进行运算，但是你定义 两个 bitset< 100>a,b 之后 直接可以对a和b进行运算 ，也可以对具体的比如a[0]和b[0]进行运算，如果不懂这个东西的话可以先学一下，学完后代码基本就能A了

#include
using namespace std;
 
const int maxn = 3000+11;
bitset<maxn>bs[maxn],p,q;
char s[maxn][maxn];
int main()
{
 
    int n,m;
    scanf("%d%d",&n,&m);
    for(int a=1;a<=n;a++)
    {
        scanf("%s",s[a]);
        for(int b=0;b<m;b++)
        {
            bs[a][b]=s[a][b]-'0';
        }
    }
    int t;
    scanf("%d",&t);
    while(t--)
    {
        char v[maxn];
        scanf("%s",v);
        for(int a=0;a<m;a++)
        {
            if(v[a]=='1')
            {
                p[a]=0;
                q[a]=1;
            }
            else if(v[a]=='0')
            {
                p[a]=0;
                q[a]=0;
            }
            else
            {
                p[a]=1;
                q[a]=1;
            }
        }
        int ant=0;
        for(int a=1;a<=n;a++)
        {
            if((p | bs[a])==q)
                ant++;
        }
        printf("%d\n",ant);
    }
    return 0;
}