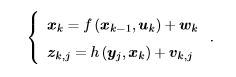《第6讲 非线性优化 》读书笔记
本文是《视觉SLAM十四讲》第6讲的个人读书笔记,为防止后期记忆遗忘写的。
本节知识脉络
- 对状态估计问题,通过概率论中贝叶斯公式,求解后验概率等价于求解最大似然函数。求解最大似然函数等价于其最小化负对数的求解。通过公式推导,引出最小二乘。问题转换为:求解最大似然,需要求解目标函数最小二乘公式。
- 最小二乘的求解需要求导,为避免求导数的巨大计算代价,采用下降迭代近似来求解问题。对于 ∆x的确定,进而引出了不同的求解方法: 一阶和二阶梯度法、Gauss-Newton、Levenberg-Marquadt等等……
- 在代码中如何实现上述各种求解方法呢?需要用到ceres和g2o第三方库。
通过第3-5讲的学习,现在我们已经知道,方程中的位姿可以由变换矩阵来描述,然后用李代数进行优化。观测方程由相机成像模型给出。然而,由于噪声的存在,运动方程和观测方程的等式必定不是精确成立的。所以,与其假设数据必须符合方程,不如来讨论,如何在有噪声的数据中进行准确的状态估计。这就是我们本章讨论的问题。
由于在 SLAM 问题中,同一个点往往会被一个相机在不同的时间内多次观测,同一个相机在每个时刻观测到的点也不止一个。这些因素交织在一起,使我们拥有了更多的约束,最终能够较好地从噪声数据中恢复出我们需要的东西。
6.1 状态估计问题
6.1.1 最大后验与最大似然
Xk 乃是相机的位姿。我们可以使用变换矩阵或李代数表示它(由 Tk 或 exp(ξ∧ k )表达)。
至于观测方程,即针孔相机模型。比如:假设在 xk 处对路标 yj 进行了一次观测,对应到 图像上的像素位置 zk,j,那么,观测方程可以表示成:
这里 K 为相机内参,s 为像素点的距离。同时这里 的 zk,j 和 yj 都必须以齐次坐标来描述。
在运动和观测方程中,我们通常假设两个噪声项 wk,vk,j 满足零均值的高斯分布。我们希望通过带噪声的数据 z 和 u,推断位姿 x 和地图 y(以 及它们的概率分布),这构成了一个状态估计问题。
很长一段时间内,研究者们使用滤波器,尤其是扩展卡尔曼滤波器(EKF)求解它。但是卡尔曼滤波器关心当前时刻的状态估计 xk,而对之前的状态则不多考虑;相对的,近年来普遍使用的非线性优化方法,使用所有时刻采集到的数据进行状态估计,并被认为优于传统的滤波器 [13],成为当前视觉 SLAM 的主流方法。
概率论上:对机器人状态的估计,就是求已知输入数据 u 和观测数据 z 的条件下,计算状态 x 的条件概率分布: 当我们没有测量运动的传感器(u就是IMU的读数), 只有一张张的图像时,即只考虑观测方程带来的数据时,相当于估计 P(x|z) 的条件概率分布。利用贝叶斯法则,有:
当我们没有测量运动的传感器(u就是IMU的读数), 只有一张张的图像时,即只考虑观测方程带来的数据时,相当于估计 P(x|z) 的条件概率分布。利用贝叶斯法则,有:
6.1.2 最小二乘的引出
-
如何求最大似然估计呢?
对于某一次观测:![]() 假设了噪声项
假设了噪声项![]() 为了计算使它最大化的 xk, yj,我们往往使用最小化负对数的方 式,来求一个高斯分布的最大似然。(这是在 求出似然函数概率 的最大概率值-->等价于求 后验函数概率 的最大概率值)
为了计算使它最大化的 xk, yj,我们往往使用最小化负对数的方 式,来求一个高斯分布的最大似然。(这是在 求出似然函数概率 的最大概率值-->等价于求 后验函数概率 的最大概率值)
对原分布求最大化相当于对负对数求最小化。第一项与 x 无 关,可以略去。于是,只要最小化右侧的二次型项,就得到了对状态的最大似然估计。代 入 SLAM 的观测模型,相当于我们在求: ![]()
该式等价于最小化噪声项(即误差)的平方(Σ 范数意义下)。
-
我们现在将运动方程和观测方程同时考虑,不再只单单考虑观测方程。
(这段话很关键)这就得到了一个总体意义下的最小二乘问题(Least Square Problem)。我们明白它的最优 解等价于状态的最大似然估计。直观来讲,由于噪声的存在,当我们把估计的轨迹与地图 代入 SLAM 的运动、观测方程中时,它们并不会完美的成立。这时候怎么办呢?我们把状态的估计值(函数中的参数)进行微调,使得整体的误差下降一些。当然这个下降也有限度,它一般会到达 一个极小值。这就是一个典型非线性优化的过程。
6.2 非线性最小二乘
现在,我们要介绍如何求解上面这个最小二乘问题。将介绍非线性优化的基本知识,特别地,针对这样一个通用的无约束非线性最小二乘问题,探讨它是如何求解的。
普通的简单最小二乘问题对其求导为0,便可求出极值。而SLAM的最小二乘并非能够简单求得。对于不方便直接求解的最小二乘问题,我们用迭代的方式,从一个初始值出发,不 断地更新当前的优化变量,使目标函数下降。具体步骤可列写如下:
这让求解导函数为零的问题,变成了一个不断寻找梯度并下降的过程。直到某个时刻 增量非常小,无法再使函数下降。此时算法收敛,目标达到了一个极小,我们完成了寻找 极小值的过程。在这个过程中,我们只要找到迭代点的梯度方向即可,而无需寻找全局导 函数为零的情况。
增量 ∆Xk如何确定?下面将分三类进行求解推导说明
6.2.1 普通的但有缺点的 一阶和二阶梯度法
一阶和二阶梯度法都十分直观,只要把函数在迭代 点附近进行泰勒展开,并针对更新量作最小化即可。将目标函数(误差平方)在 x 附近进行泰勒展开:
这里 J 是 ∥f(x)∥ ^2关于 x 的导数(雅可比矩阵),而 H 则是二阶导数(海塞(Hessian) 矩阵)。
如果保留一阶梯度,那么增量的方向为:![]() 它的直观意义非常简单,只要我们沿着反向梯度方向前进即可。当然,我们还需要该方向上取一个步长 λ,求得最快的下降方式。这种方法被称为最速下降法。
它的直观意义非常简单,只要我们沿着反向梯度方向前进即可。当然,我们还需要该方向上取一个步长 λ,求得最快的下降方式。这种方法被称为最速下降法。
求右侧等式关于 ∆x 的导数并令它为零(求导为0求出后面关于∆x 的极小值,便可求出增量方程的最小值),就得到了增量的解:![]() 该方法称又为牛顿法。
该方法称又为牛顿法。
不过,这两种方法也存在它们自身的问题。最速下降法过于贪心,容易走出锯齿路线,反 而增加了迭代次数。而牛顿法则需要计算目标函数的 H 矩阵,这在问题规模较大时非常 困难,我们通常倾向于避免 H 的计算。
6.2.2 Gauss-Newton
它的思想是将 f(x) 进行一阶的 泰勒展开(请注意不是目标函数 f(x) 2):![]() 这里 J(x) 为 f(x) 关于 x 的导数,实际上是一个 m × n 的矩阵,也是一个雅可比矩 阵。为了求 ∆x,我们需要解一个线性的最小二乘问题:
这里 J(x) 为 f(x) 关于 x 的导数,实际上是一个 m × n 的矩阵,也是一个雅可比矩 阵。为了求 ∆x,我们需要解一个线性的最小二乘问题:
我们要求解的变量是 ∆x,因此这是一个线性方程组,我们称它为增量方程,也 可以称为高斯牛顿方程。我 们把左边的系数定义为 H,右边定义为 g,那么上式变为:![]()
对比牛顿法可见,Gauss-Newton 用 ![]() 作为牛顿法中 二阶 Hessian 矩阵的近似,从而省略了计算 H 的过程。求解增量方程是整个优化问题的 核心所在。那么 Gauss-Newton 的算法步骤可以写成:
作为牛顿法中 二阶 Hessian 矩阵的近似,从而省略了计算 H 的过程。求解增量方程是整个优化问题的 核心所在。那么 Gauss-Newton 的算法步骤可以写成:
存在问题问题:在使用 Gauss Newton 方法时,可能出现 ![]() 为奇异矩阵或者病态 (illcondition) 的情况,此时增量的稳定性较差,导致算法不收敛。更严重的是,就算我们假 设 H 非奇异也非病态,如果我们求出来的步长 ∆x 太大,也会导致我们采用的局部近似 (6.19) 不够准确,这样一来我们甚至都无法保证它的迭代收敛,哪怕是让目标函数变得更 大都是有可能的。
为奇异矩阵或者病态 (illcondition) 的情况,此时增量的稳定性较差,导致算法不收敛。更严重的是,就算我们假 设 H 非奇异也非病态,如果我们求出来的步长 ∆x 太大,也会导致我们采用的局部近似 (6.19) 不够准确,这样一来我们甚至都无法保证它的迭代收敛,哪怕是让目标函数变得更 大都是有可能的。
6.2.3 Levenberg-Marquadt
Levenberg-Marquadt 方法在一定程度上修正了这些问题,一般认为它比 Gauss Newton 更为鲁棒。尽管它的收敛速度可能会比 Gauss Newton 更慢,被称之为阻尼牛顿法。
信赖区域:由于 Gauss-Newton 方法中采用的近似二阶泰勒展开只能在展开点附近有较好的近似 效果,所以我们很自然地想到应该给 ∆x 添加一个信赖区域(Trust Region),不能让它太 大而使得近似不准确。非线性优化种有一系列这类方法,这类方法也被称之为信赖区域方 法 (Trust Region Method)。在信赖区域里边,我们认为近似是有效的;出了这个区域,近 似可能会出问题。
近似范围的动态收缩判断:我们使用 来进行衡量判断。ρ 的分子是实际函数下降的值,分母是近似模型下降的值。如 果 ρ 接近于 1,则近似是好的。如果 ρ 太小,说明实际减小的值远少于近似减小的值,则 认为近似比较差,需要缩小近似范围。反之,如果 ρ 比较大,则说明实际下降的比预计的 更大,我们可以放大近似范围。
来进行衡量判断。ρ 的分子是实际函数下降的值,分母是近似模型下降的值。如 果 ρ 接近于 1,则近似是好的。如果 ρ 太小,说明实际减小的值远少于近似减小的值,则 认为近似比较差,需要缩小近似范围。反之,如果 ρ 比较大,则说明实际下降的比预计的 更大,我们可以放大近似范围。
Levenberg-Marquadt的迭代过程:
在 L-M 优化中,我们都需要解式(6.24)那样一个子问题来获得梯度。这 个子问题是带不等式约束的优化问题,我们用 Lagrange 乘子将它转化为一个无约束优化 问题:
这里 λ 为 Lagrange 乘子。类似于 Gauss-Newton 中的做法,把它展开后,我们发现 该问题的核心仍是计算增量的线性方程:![]() 。
。
当参数 λ 比较小时,H 占主要地位,这说明二次近似模型在该范围内是比 较好的,L-M 方法更接近于 G-N 法。另一方面,当 λ 比较大时,λI 占据主要地位,L-M 更接近于一阶梯度下降法(即最速下降),这说明附近的二次近似不够好。L-M 的求解方 式,可在一定程度上避免线性方程组的系数矩阵的非奇异和病态问题,提供更稳定更准确 的增量 ∆x。
非线性优化问题的框架,分为 Line Search 和 Trust Region 两类。Line Search 先固 定搜索方向,然后在该方向寻找步长,以最速下降法和 Gauss-Newton 法为代表。而 Trust Region 则先固定搜索区域,再考虑找该区域内的最优点。此类方法以 L-M 为代表。实际 问题中,我们通常选择 G-N 或 L-M 之一作为梯度下降策略。
非线性优化问题都要提供初始值,但是取得初始值也是有具体的章法的,比如ICP和PnP方法等等。因为上面等式中有矩阵元素,所以上述的式子其实是一方程组。对于高维方程组的求解,涉及到计算力资源和时间的问题。后期将用矩阵分割或者稀疏矩阵的形式进行解决。
6.3 实践:Ceres
对于线性优化问题的求解,使用两个来自谷歌的 C++ 的优化库:Ceres 库 和g2o 库。
在这个问题中,优化变 量为 x1, . . . , xn,fi 称为代价函数(Cost function),在 SLAM 中亦可理解为误差项。lj 和 uj 为第 j 个优化变量的上限和下限。
在 Ceres 中,我们只要定义优化变量 x 和每个代价函数 fi,再调用 Ceres 进行求解。我 们可以选择使用 G-N 或者 L-M 进行梯度下降,并设定梯度下降的条件。Ceres 会在优化 之后,将最优估计值返回给我们。
6.3.3 使用 Ceres 拟合曲线
假设有一条满足以下 方程的曲线:![]() 其中 a, b, c 为曲线的参数,w 为高斯噪声。假设我们有 N 个关于 x, y 的观测数据点,想根据这些数据点求 出曲线的参数。那么,可以求解下面的最小二乘问题以估计曲线参数:
其中 a, b, c 为曲线的参数,w 为高斯噪声。假设我们有 N 个关于 x, y 的观测数据点,想根据这些数据点求 出曲线的参数。那么,可以求解下面的最小二乘问题以估计曲线参数: 。(待估计的变量是 a, b, c,而不是 x。)
。(待估计的变量是 a, b, c,而不是 x。)
下述代码中,复制了《视觉SLAM十四讲》中的章节。
#include
#include
#include
#include
using namespace std;
// 代价函数的计算模型
struct CURVE_FITTING_COST
{
CURVE_FITTING_COST ( double x, double y ) : _x ( x ), _y ( y ) {}
template bool operator() (const T* const abc, T* residual ) const // 残差的计算
{
residual[0] = T ( _y ) - ceres::exp ( abc[0]*T ( _x ) *T ( _x ) + abc[1]*T ( _x ) + abc[2] ); // y-exp(ax^2+bx+c)
return true;
}
const double _x, _y; // x,y数据
};
int main ( int argc, char** argv )
{
double a=1.0, b=2.0, c=1.0; // 真实参数值
int N=100; // 数据点
double w_sigma=1.0; // 噪声Sigma值
cv::RNG rng; // OpenCV随机数产生器
double abc[3] = {0,0,0}; // abc参数的估计值
vector x_data, y_data; // 数据
cout<<"*************generating data: **********"< (
new CURVE_FITTING_COST ( x_data[i], y_data[i] )
),
nullptr, // 核函数,这里不使用,为空
abc // 待估计参数
);
}
// 配置求解器
ceres::Solver::Options options; // 这里有很多配置项可以填
options.linear_solver_type = ceres::DENSE_QR; // 泰勒展开后,增量方程如何求解
options.minimizer_progress_to_stdout = true; // 输出到cout
ceres::Solver::Summary summary; // 优化信息
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
ceres::Solve ( options, &problem, &summary ); // 开始优化
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
//计算时间
chrono::duration time_used = chrono::duration_cast>( t2-t1 );
cout<<"solve time cost = "< 6.4 实践:g2o
为什么要引入图优化:
我们并不清楚误差项和变量之间的关联。比方说,某一个 优化变量 xj 存在于多少个误差项里呢?我们能保证对它的优化是有意义的吗?我们希望能够直观地看到该优化问题长什么样。于是,就说到了图优化。于是用顶点表示优化变量,用边表示误差项。我们可以利用图模型的某些性质,做更好的优化。
在上述问题中,整个问题只有一个顶点:曲线模型的参数 a, b, c;而每个带噪声的 数据点,构成了一个个误差项,也就是图优化的边。我们要做的事主要有以下几个步骤:
下述代码中,复制了《视觉SLAM十四讲》中的章节。里面定义的类存在继承关系,部分父类可看g2o源码加深理解,代码有些晦涩,不易懂。
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
// 曲线模型的顶点,模板参数:优化变量维度和数据类型
class CurveFittingVertex: public g2o::BaseVertex<3, Eigen::Vector3d> //继承 BaseVertex
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
virtual void setToOriginImpl() // 重置
{
_estimate << 0,0,0;
}
virtual void oplusImpl( const double* update ) // 更新 处理的是 xk+1 = xk + ∆x 的过程。
{
_estimate += Eigen::Vector3d(update);
}
// 存盘和读盘:留空
virtual bool read( istream& in ) {}
virtual bool write( ostream& out ) const {}
};
// 误差模型\模型的边 模板参数:观测值维度,类型,连接顶点类型
class CurveFittingEdge: public g2o::BaseUnaryEdge<1,double,CurveFittingVertex>
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
CurveFittingEdge( double x ): BaseUnaryEdge(), _x(x) {}
// 计算曲线模型误差。取出边所连接的顶点的当前估计值,根据曲线模型,与它的观测值进行比较。
void computeError()
{
//得到定点数组
const CurveFittingVertex* v = static_cast (_vertices[0]);
const Eigen::Vector3d abc = v->estimate();
_error(0,0) = _measurement - std::exp( abc(0,0)*_x*_x + abc(1,0)*_x + abc(2,0) ) ;
}
virtual bool read( istream& in ) {}
virtual bool write( ostream& out ) const {}
public:
double _x; // x 值, y 值为 _measurement
};
int main( int argc, char** argv )
{
//产生观测值数据
double a=1.0, b=2.0, c=1.0; // 真实参数值
int N=100; // 数据点
double w_sigma=1.0; // 噪声Sigma值
cv::RNG rng; // OpenCV随机数产生器
double abc[3] = {0,0,0}; // abc参数的估计值
vector x_data, y_data; // 数据
cout<<"generating data: "< > Block; // 每个误差项优化变量维度为3,误差值维度为1
Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense(); // 线性方程求解器
Block* solver_ptr = new Block( linearSolver ); // 矩阵块求解器
// 梯度下降方法,从GN, LM, DogLeg 中选
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg( solver_ptr );
// g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr );
// g2o::OptimizationAlgorithmDogleg* solver = new g2o::OptimizationAlgorithmDogleg( solver_ptr );
g2o::SparseOptimizer optimizer; // 图模型
optimizer.setAlgorithm( solver ); // 设置求解器
optimizer.setVerbose( true ); // 打开调试输出
// 往图中增加顶点
CurveFittingVertex* v = new CurveFittingVertex();
v->setEstimate( Eigen::Vector3d(0,0,0) );
v->setId(0);
optimizer.addVertex( v );
// 往图中增加边
for ( int i=0; isetId(i);
edge->setVertex( 0, v ); // 设置连接的顶点
edge->setMeasurement( y_data[i] ); // 观测数值
edge->setInformation( Eigen::Matrix::Identity()*1/(w_sigma*w_sigma) ); // 信息矩阵:协方差矩阵之逆
optimizer.addEdge( edge );
}
// 执行优化
cout<<"start optimization"< time_used = chrono::duration_cast>( t2-t1 );
cout<<"solve time cost = "<estimate();
cout<<"estimated model: "<