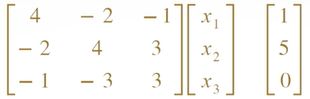[MATLAB]线性方程组求解(雅可比迭代和高斯迭代源码实现)
本试验取材于中南大学《科学计算与MATLAB语言》。
直接解法
- 高斯消去法
- 列主元消去法
- 矩阵的三角分解法
(1)利用左除运算符的直接解法
Ax=b------>x=a\b
注意:如果矩阵A是奇异的或接近奇异的,则MATLAB会给出警告信息。
![[MATLAB]线性方程组求解(雅可比迭代和高斯迭代源码实现)_第1张图片](http://img.e-com-net.com/image/info8/e0ed4899b2c0410f9407b195202455fa.jpg)
>> A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];
>> b=[13,-9,6,0]';
>> x=A\b
x =
-66.5556
25.6667
-18.7778
26.5556
(2)利用矩阵分解求解线性方程组
>> A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];
>> b=[13,-9,6,0]';
>> [L,U]=lu(A);
>> x=U\(L\b)
x =
-66.5556
25.6667
-18.7778
26.5556
>>
迭代解法
- 雅可比(Jacobi)迭代法
- 高斯-赛德尔(Gauss-Serdel)迭代法
这里先讲一下雅可比迭代法,雅可比迭代法,特别花里胡哨,但是我在求复合函数偏导数特别好使,因此下面给出雅可比迭代法的具体实现步数
![[MATLAB]线性方程组求解(雅可比迭代和高斯迭代源码实现)_第6张图片](http://img.e-com-net.com/image/info8/18e4d18a9fb94e7eb12fea708d880e44.jpg)
创建一个jacobi.m
function [y,n]=jacobi(A,b,x0,ep)
%%输出的参数 y指方程的解 n为迭代的次数
% 输入的参数分别是系数矩阵 右端列向量 迭代的初值 精度
D=diag(diag(A))%%求对角矩阵
L=-tril(A,-1);%%求下三角
U=-triu(A,1);%%求上三角
B=D\(L+U);
f=D\b;
y=B*x0+f;
n=1;
while norm(y-x0)>=ep %%用2范数去逼近
x0=y;
y=B*x0+f;
n=n+1;
end
这段代码巧妙实现了雅可比迭代算法流程
(2)高斯–赛德尔(Gauss-Serdel)迭代法
第二种方法是站在第一种方法基础上,将代码稍微更改,直接变成高斯—赛德尔迭代法.
![[MATLAB]线性方程组求解(雅可比迭代和高斯迭代源码实现)_第7张图片](http://img.e-com-net.com/image/info8/b046896cce0e478dbd710138f62f5fc6.jpg)
创建一个gauseidel.m
function [y,n]=gauseidel(A,b,x0,ep)
D=diag(diag(A))%%求对角矩阵
L=-tril(A,-1);%%求下三角
U=-triu(A,1);%%求上三角
B=(D-L)\U;
f=(D-L)\b;
y=B*x0+f;
n=1;
while norm(y-x0)>=ep %%用2范数去逼近
x0=y;
y=B*x0+f;
n=n+1;
end
>> A=[4,-2,-1;-2,4,3;-1,-3,3];
>> b=[1,5,0]';
>> [x,n]=jacobi(A,b,[0,0,0]',1.0e-6)
x =
0.9706
0.8529
1.1765
n =
35
>> [x,n]=gauseidel(A,b,[0,0,0]',1.0e-6)
x =
0.9706
0.8529
1.1765
n =
16
>>
小结:虽然你可以看到感觉高斯迭代次数更少,可以直接迭代出更雅可比一样的值,但现实是两者无法作为比较,一种可能连收敛性都无法确定。
![[MATLAB]线性方程组求解(雅可比迭代和高斯迭代源码实现)_第8张图片](http://img.e-com-net.com/image/info8/d4903f0200464ab48a2a2eb5cfb0af22.jpg)
>> A=[1,2,-2;1,1,1;2,2,1];
>> b=[9;7;6];
>> [x,n]=jacobi(A,b,[0;0;0],1.0e-6)
x =
-27
26
8
n =
4
>> [x,n]=gauseidel(A,b,[0;0;0],1.0e-6)
x =
1.0e+305 *
-Inf
Inf
-1.7556
n =
1011
>>
相信各位看官看见了,高斯迭代竟然不收敛!
![[MATLAB]线性方程组求解(雅可比迭代和高斯迭代源码实现)_第2张图片](http://img.e-com-net.com/image/info8/97b26eebd74945e1920c13e7f2e09a11.jpg)
![[MATLAB]线性方程组求解(雅可比迭代和高斯迭代源码实现)_第3张图片](http://img.e-com-net.com/image/info8/122e07cb1c814f3a8c3f71959dc1a7b9.jpg)
![[MATLAB]线性方程组求解(雅可比迭代和高斯迭代源码实现)_第4张图片](http://img.e-com-net.com/image/info8/6e5f86a95ecc4e639e6e9071743d9282.jpg)
![[MATLAB]线性方程组求解(雅可比迭代和高斯迭代源码实现)_第5张图片](http://img.e-com-net.com/image/info8/955c616084214bfd9d59d21a9a16ecc6.jpg)