数学建模:matlab解决线性规划问题
在人们的生产实践中,经常会遇到如何利用现有资源来安排生产,以取得最大经济效
益的问题。此类问题构成了运筹学的一个重要分支一数学规划,而线性规划(Linear
Programming, LP)则是数学规划的一个重要分支。自从1947年G. B. Dantzig 提出求解线
性规划的单纯形方法以来,线性规划在理论上趋向成熟,在实用中日益广泛与深入。特别
是在计算机能处理成千上万个约束条件和决策变量的线性规划问题之后,线性规划的适
用领域更为广泛了,已成为现代管理中经常采用的基本方法之一。
例如,给定m个数据点(xi,yi),i=1,2,…,m,拟合一条直线y=ax+b(即确定参数a、b),使得所有数据点(xi,yi)和拟合直线上对应的点(xi,axi+b)之间距离的最大值rmax最小。也就是说,对整个这组数据点而言,最大绝对偏差r=max{ | yi-y(xi) | }最小。这种准则实际上定义了如下优化问题:
M i n r Min\;\;r Minr
s . t . s.t. s.t.
f ( n ) = { r − r i ≥ 0 , r + r i ≥ 0 , i = 1 , 2 , . . . , m f(n)= \begin{cases}r-r_i\geq0, \\ r+r_i\geq0, \end{cases} \\ i=1,2,...,m f(n)={r−ri≥0,r+ri≥0,i=1,2,...,m
这是一个线性规划问题,具有很广泛的应用。
木匠问题
木匠销售桌子和书架的单位净利润分别为25美元和30美元,他希望确定每周生产的桌子数量x和书架数量y。他每周最多有690 张木板和120小时的劳动时间可以利用,如果木板和工时不用于生产桌子和书架,他能够将它们有效地使用在其他方面。他估计,生产一张桌子需要20张木板和5小时劳动时间,生产一个书架需要30张木板和4小时劳动时间。模型为
M a x 25 x + 30 y Max\;25x+30y Max25x+30y
s . t . s.t. s.t.
20 x + 30 y ≤ 690 ( 木 板 ) 5 x + 4 y ≤ 120 ( 劳 动 时 间 ) x , y ≥ 0 ( 非 劳 动 性 ) 20x+30y\leq690\qquad(木板)\\ 5x+4y\leq120\qquad(劳动时间)\\ x,y\geq0\qquad(非劳动性) 20x+30y≤690(木板)5x+4y≤120(劳动时间)x,y≥0(非劳动性)
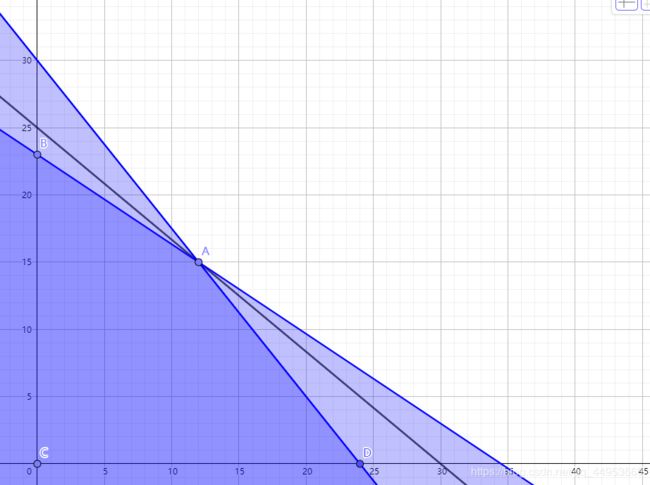
木匠问题中的约束所代表的凸集在图中用多边形ABCD表示。请注意,约束所代表的直线有6个交点,但只有四个交点(即A—D)满足所有约束从而属于该凸集。点A—D是该多边形的极点。
如果一个线性规划存在最优解,它必然也会出现在约束所形成的凸集的某个极点上,极点上目标函数的值(木匠问题的利润)是
| 极点 | 目标函数值(美元) |
|---|---|
| A(12,15) | 750 |
| B(0,23) | 690 |
| C(0,0) | 0 |
| D(24,0) | 600 |
因此,木匠每周应该制作12张桌子和15个支架,每周最大利润为750美元。
木匠问题(线性规划)的matlab解法
线性规划的目标函数可以是求最大值,也可以是求最小值,约束条件的不等号可以是
小于等号也可以是大于等号。为了避免这种形式多样性带来的不便, Matlab中规定线性
规划的标准形式为
m i n f T x min\;f^Tx minfTx
s . t . = { A ⋅ x ≤ 0 , A e q ⋅ x = b e q ≥ 0 , l b ≤ x ≤ u b s.t.= \begin{cases}A·x\leq0, \\ Aeq·x=beq\geq0, \\lb\leq x\leq ub \end{cases} s.t.=⎩⎪⎨⎪⎧A⋅x≤0,Aeq⋅x=beq≥0,lb≤x≤ub
式中:f,x ,b ,beq,lb, ub为列向量,其中f称为价值向量,b称为资源向量;A , Aeq为矩阵。
Matlab中求解线性规划的命令为
[x,fval] = linprog(f,A,b)
[x,fval] = linprog( f,A,b,Aeq, beq)
[x,fval] = linprog( f ,A, b,Aeq , beq,1b,ub)
式中:x返回决策向量的取值;fval返回目标函数的最优值;f为价值向量;A和b对应线性
不等式约束;Aeq和beq对应线性等式约束;lb和ub分别对应决策向量的下界向量和上
界向量。
例如,线性规划
m a x c T x , s . t . A x ≥ b max\;c^Tx, \\s.t.\;\;Ax\geq b maxcTx,s.t.Ax≥b
的matlab标准型为
m i n − c T x , s . t . − A x ≤ − b min\;-c^Tx, \\s.t.\;\;-Ax\leq -b min−cTx,s.t.−Ax≤−b
附上木桶问题的matlab代码
f=[ -25; -30];
a=[ 20,30;5,4]; b=[690;120];
[x,y] =linprog( f ,a,b,[], [], zeros(2,1));
x,y=-y
x =
12.0000
15.0000
y =
750
转载请标明出处,谢谢!。
如果感觉本文对您有帮助,请留下您的赞,您的支持是我坚持写作最大的动力,谢谢!