【图论·算法】树的直径&重心概念与求解
树的直径
树是连通无环图,树上任意两点之间的路径是唯一的。定义树上任意两点u; v的距离为u到v路径上边权的和。树的直径MN为树上最长路径,即点M和N是树上距离最远的两个点。此时,树的直径也称树的最长链。
NO.1树形DP求树的直径
我们设f[i]表示以i为根节点的所有子树中,与i距离最远的一个节点的路径。
状态转移方程为: f [ i ] = m a x ( f [ j ] + v a l ( i , j ) ) , j ∈ s o n ( i ) f[i]=max(f[j]+val(i,j)),j∈son(i) f[i]=max(f[j]+val(i,j)),j∈son(i)
表示以子树为根节点的最大路径与当前根节点连边后的最大值即为当前的最大值。
此时我们思考树的直径怎么求。
 在这个图里·,我们求解f[1]时,通过枚举顺序,我们已经枚举到了节点3,且节点2已经被访问。
在这个图里·,我们求解f[1]时,通过枚举顺序,我们已经枚举到了节点3,且节点2已经被访问。
此时节点2和节点3的动态规划已经完成,假如是如图所示的红色部分为动态规划决策的边集。
而f[1][1]则已经连通了其中的一边,找到了一个不一定是最优的解。此时绿色和红色的边是f[1]一组合法的解。
通过观察,我们可以发现树的直径其实就是左子树中标有颜色的边+v(1,3)+右子树标有颜色的点,也就是f[1]+v(1,3)+f[3].
因此在枚举i和儿子j时,直径 D = m a x ( f [ i ] + v a l + f [ j ] ) D=max(f[i]+val+f[j]) D=max(f[i]+val+f[j]).
代码如下:
#include两次搜索求树的直径
对于搜索,我们可以选择DFS也可以选择BFS;为了避免栈溢出,我们在这里选择了BFS。
具体做法是:
- B F S 1 : BFS1: BFS1:随意选取一个根节点,找到离根节点最远的点 M M M.
- B F S 2 : BFS2: BFS2:找出离 M M M最远的点 N N N,此时 V ∣ M → N ∣ V|M→N| V∣M→N∣为树的直径。
此时我们需要证明这个算法的正确性,选用反证法进行证明。
证明:
假设M不是直径的一个端点,AB是树的直径。
当P在直径上时,如图所示:
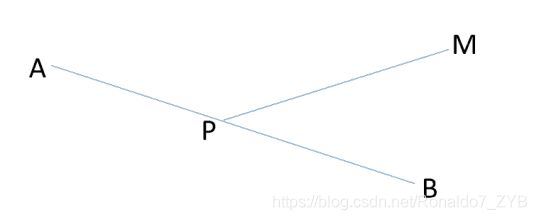
则 P M > P B → A P + P M > P B + P M → A P + P M > A B PM>PB→AP+PM>PB+PM→AP+PM>AB PM>PB→AP+PM>PB+PM→AP+PM>AB.
此时AB不是树的直径,与已知矛盾。
当P不在直径上,且PM和AB有公共点T,如图所示:
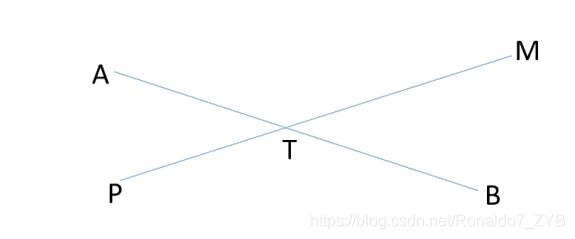
此时 P T + T M > T M + T B → P T > T B 。 PT+TM>TM+TB→PT>TB。 PT+TM>TM+TB→PT>TB。
则 P T + A T > A T + T B → P T + A T > A B PT+AT>AT+TB→PT+AT>AB PT+AT>AT+TB→PT+AT>AB,此时AB不是树的直径,于已知矛盾。
当p在直径外切PM和AB没有公共点,如图所示:

P C + C M > P C + C D + B D → C M > C D + B D , PC + CM > PC + CD + BD→CM > CD + BD, PC+CM>PC+CD+BD→CM>CD+BD,
C M + C D > B D → C M + C D + A D > B D + A D = A B CM + CD > BD →CM + CD + AD > BD + AD = AB CM+CD>BD→CM+CD+AD>BD+AD=AB此时AB不是树的直径,于已知矛盾。
综上所述,上述算法是正确的。
代码如下:
#include树的重心
树的重心也叫树的质心。找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心,删去重心后,生成的多棵树尽可能平衡。
最大的子树节点最少,这一性质非常容易理解。
- 易错误区:对于平衡的理解。
如图所示,我们来理解一下平衡的概念:
左边是各个子树相对的平衡,而右边是分成两堆子树后相对平衡;此时树的重心应该是左边的一种。是各个子树的相对平衡。
我们来说一下树的重心的求法:
- 处理一个数子树的个数
- 处理一个数子树的最大值
- 对子树的最大值进行比较,最小的即为树的重心
- 这里可以使用dfs的方式求解
代码如下:
#include