pojAntenna Placement【二分图-最小边覆盖】

题意

一个矩形中，有N个城市’*’，现在这n个城市都要覆盖无线，若放置一个基站，那么它至多可以覆盖相邻的两个城市。问至少放置多少个基站才能使得所有的城市都覆盖无线？

分析

将一个基站表示一条边，相邻的两点连接起来。这样就得到一个模型，求一个无向图用最少的边覆盖。即是一个二分图最小边覆盖问题

几个概念

边覆盖集：通俗地讲，所谓边覆盖集，就是G中所有的顶点都是E中某条边的邻接顶点（边覆盖顶点），一条边只能覆盖2个顶点。
注意： 在无向图中存在用尽量少的边去“覆盖”住所有的顶点，所以边覆盖集有极小与最小的区别
极小边覆盖： 若边覆盖E 中的任何真子集都不是边覆盖集，则称E是极小边覆盖集。
最小边覆盖： 边数最小的边覆盖称为最小边覆盖，通俗地讲，就是极小边覆盖中的最小的一个集合
最小边覆盖= 最大独立集 = n - 最大匹配
无向图的最小边覆盖 = (二分图两边顶点数 - 二分图的最大匹配数)/2.

回到本题

如何将无向图最小边覆盖问题转化为二分图的最小边覆盖问题

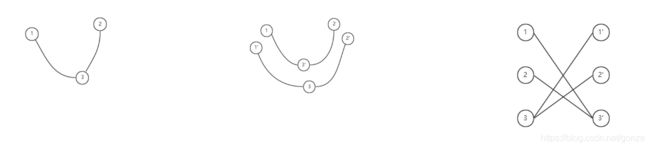
这里经过一个叫做拆点的操作，其实就是将原图复制了一份，显而易见，拆点后图的最小边覆盖数是原图的两倍。注意观察里面点的命名，一条边总是连接一个实点和一个虚点（二分图一条边总是连接左边的点 和 右边的点）

构图

在本题中我们可以将虚点表示为矩形的下半部分，于是可以简化这个建图
具体做法：
1、将所有的城市（*）从1开始标记
2、将相邻的点且标记为数字的，连接起来

参考代码

#include
#include
#include
#include
#include
#include
using namespace std;
#define ll long long
#define in rad()
inline int rad(){
	int x=0,f=1;char c=getchar();while(c>'9'||c<'0')c=getchar();
	if(c=='-')f=-1,c=getchar();while(c>='0'&&c<='9')x=x*10+c-48,c=getchar();
	return x*f;
}
const int maxn=1e3+10;
const int inf=1e9;
int t,r,c,tot=0;char s[100];
int mp[maxn][maxn],g[maxn][maxn];
int vis[maxn],match[maxn];
int dx[]={0,0,-1,1};
int dy[]={1,-1,0,0};
int find(int x){
	for(int i=1;i<=tot;i++){
		if(vis[i]||g[x][i]==0)continue;
		vis[i]=1;
		if(match[i]==-1 || find(match[i])){
			match[i]=x;return 1;
		}
	}
	return 0;
}
int km(){
	int ret=0;
	memset(match,-1,sizeof(match));
	for(int i=1;i<=tot;i++){
		memset(vis,0,sizeof(vis));
		ret+=find(i); 
	}
	return ret;
}
int main(){
	t=in;
	while(t--){
		tot=0;memset(mp,0,sizeof(mp));memset(g,0,sizeof(g));
		r=in;c=in;
		for(int i=1;i<=r;i++){
			scanf("%s",s+1);
			for(int j=1;j<=c;j++)
				if(s[j]=='*')mp[i][j]=++tot;			
		}
		for(int i=1;i<=r;i++)
			for(int j=1;j<=c;j++)
				if(mp[i][j]){
					for(int k=0;k<4;k++){
						int x=i+dx[k],y=j+dy[k];
						if(!mp[x][y])continue;
						g[mp[i][j]][mp[x][y]]=1;//无向变双向，相当于拆点 
					}
				}	
		int ans=tot-km()/2;
		printf("%d\n",ans); 
	}
	return 0;
}