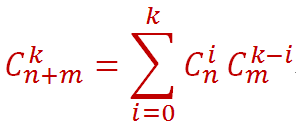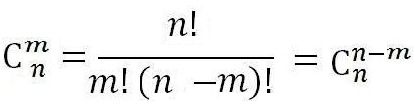【组合数-逆元】CF-785D Anton and School - 2
前言
逆元和组合数我屡了半天才弄清楚...赶紧码个博客记录来之不易的“理解”
题目
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
As you probably know, Anton goes to school. One of the school subjects that Anton studies is Bracketology. On the Bracketology lessons students usually learn different sequences that consist of round brackets (characters "(" and ")" (without quotes)).
On the last lesson Anton learned about the regular simple bracket sequences (RSBS). A bracket sequence s of length n is an RSBS if the following conditions are met:
- It is not empty (that is n ≠ 0).
- The length of the sequence is even.
- First
charactes of the sequence are equal to "(". - Last charactes of the sequence are equal to ")".
For example, the sequence "((()))" is an RSBS but the sequences "((())" and "(()())" are not RSBS.
Elena Ivanovna, Anton's teacher, gave him the following task as a homework. Given a bracket sequence s. Find the number of its distinct subsequences such that they are RSBS. Note that a subsequence of s is a string that can be obtained from s by deleting some of its elements. Two subsequences are considered distinct if distinct sets of positions are deleted.
Because the answer can be very big and Anton's teacher doesn't like big numbers, she asks Anton to find the answer modulo 109 + 7.
Anton thought of this task for a very long time, but he still doesn't know how to solve it. Help Anton to solve this task and write a program that finds the answer for it!
Input
The only line of the input contains a string s — the bracket sequence given in Anton's homework. The string consists only of characters "(" and ")" (without quotes). It's guaranteed that the string is not empty and its length doesn't exceed 200 000.
Output
Output one number — the answer for the task modulo 109 + 7.
Examples
Sample Input 1
)(()()Sample Output 1
6Sample Input 2
()()()Sample Output 2
7Sample Input 3
)))Sample Output 3
0
Note
In the first sample the following subsequences are possible:
- If we delete characters at the positions 1 and 5 (numbering starts with one), we will get the subsequence "(())".
- If we delete characters at the positions 1, 2, 3 and 4, we will get the subsequence "()".
- If we delete characters at the positions 1, 2, 4 and 5, we will get the subsequence "()".
- If we delete characters at the positions 1, 2, 5 and 6, we will get the subsequence "()".
- If we delete characters at the positions 1, 3, 4 and 5, we will get the subsequence "()".
- If we delete characters at the positions 1, 3, 5 and 6, we will get the subsequence "()".
The rest of the subsequnces are not RSBS. So we got 6 distinct subsequences that are RSBS, so the answer is 6.
题目大意
给一组只含 “(”和“)”的字符串，你可以删去其中一些位置的括号，也可以不删，使得剩下的括号成为“正则括号序列regular simple bracket sequences(RSBS)”：
(1) "()"是一个RSBS。
(2)如果X是一个RSBS，那么"(X)"也是一个RSBS。
(3)同时满足(1)和(2)的括号组是RSBS。
删除不同位置括号得到RSBS算作是不同的方法，问有多少种方法能让原来的字符串变成RSBS。答案模 10^9+7
输入括号串长度不超过2*10^5
PS.题目中要求的合法括号序列不能并列，如：(())()，()()都不行，((()))，(())才可以
分析
先记录每个字符左边有多少个'('，右边有多少个')'，包含当前字符本身；
然后从左往右遍历字符串，如果当前字符是'('，左边（包含本身）有a个'('，右边有b个')'，
大概如下图，其中橘色括号个数为a，蓝色括号个数为b
那么满足条件的子字符串就增加了：
一些细节：（自己辛苦分析总结而得的QAQ）
1.当前的括号 i 已经被选定了，于是可以选择的左括号数就为 a - 1
2.右括号选的个数 = 左括号选的个数 +1
3.0<=x<=a-1，0<=x+1<=b ——> 0<=x<=min(a-1,b-1)
4.由最后一个等号左边到等号右边是根据范德蒙恒等式
关于“范德蒙恒等式”，用式子表示大致是这样的：
又因为组合数的形式可以是这样的：
所以 
换成代码中的变量名就是：
由于数太大了，题目要求对mod取模，但取模时不能用除法，于是要想办法——用逆元
看了N篇博客后终于找到一篇我能看懂的了qwq，码一下：
https://blog.csdn.net/qie_wei/article/details/78571191
这个博客是对“逆元”的详细讲解，十分有用：https://blog.csdn.net/u011815404/article/details/81298032
代码
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN=200000,mod=1e9+7;
ll l[MAXN+5],r[MAXN+5],fac[MAXN+5];
char a[MAXN+5];
ll n,ans;
void Prepare()
{
fac[0]=1;
for(int i=1;i<=MAXN;i++)
fac[i]=(fac[i-1]*i)%mod;
}
ll Quick_mod(ll a,ll b,ll mod)
{
ll ret=1;
while(b)
{
if(b&1)
ret=ret*a%mod;
a=a*a%mod;
b>>=1;
}
return ret;
}
int main()
{
Prepare();
scanf("%s",a+1);
n=strlen(a+1);
for(int i=1;i<=n;i++)
{
if(a[i]=='(')
l[i]=l[i-1]+1;
else
l[i]=l[i-1];
}
for(int i=n;i>=1;i--)
{
if(a[i]==')')
r[i]=r[i+1]+1;
else
r[i]=r[i+1];
}
for(int i=1;i<=n;i++)
if(a[i]=='(')
{
ll tmp=(fac[l[i]]*fac[r[i]-1])%mod;
tmp=Quick_mod(tmp,mod-2,mod);
ans=(ans+fac[l[i]+r[i]-1]*tmp%mod)%mod;
}
printf("%lld",ans);
return 0;
}