Cell Distance（数论）

题目描述
We have a grid of squares with N rows and M columns. Let (i,j) denote the square at the i-th row from the top and j-th column from the left. We will choose K of the squares and put a piece on each of them.
If we place the K pieces on squares (x1,y1), (x2,y2), …, and (xK,yK), the cost of this arrangement is computed as:

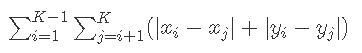
Find the sum of the costs of all possible arrangements of the pieces. Since this value can be tremendous, print it modulo 10⁹+7.
We consider two arrangements of the pieces different if and only if there is a square that contains a piece in one of the arrangements but not in the other.

Constraints
·2≤N×M≤2×10⁵
·2≤K≤N×M
·All values in input are integers.

输入
Input is given from Standard Input in the following format:

N M K

输出
Print the sum of the costs of all possible arrangements of the pieces, modulo 10⁹+7.

样例输入
2 2 2

样例输出
8

思路
本题通过计算两个块之间的曼哈顿距离来计算总贡献，因此可以通过已知结论任意两个块之间的曼哈顿距离的平均值为(n+m)/3来求得结果，已知从nm个块中任意选择k个块为C(nm,k),从k个块中任意选择2个块为
C(k,2),所以结果为C(n * m,k) * C(k,2) * (n+m)/3

代码实现

#pragma GCC optimize(3,"Ofast","inline")
#include
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int N=200005;
const int M=4005;
const ll INF=1e14;
const ull sed=31;
const ll mod=1e9+7;
const double eps=1e-12;
typedef pair<int,int>P;
 
ll n,m,k;
ll fac[N],inv[N];
 
ll qpow(ll a,ll b)
{
    ll ret=1;
    while(b)
    {
        if(b&1) ret=ret*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return ret;
}
 
void init()
{
    fac[0]=1;
    for(int i=1;i<N;i++) fac[i]=fac[i-1]*i%mod;
    inv[N-1]=qpow(fac[N-1],mod-2);
    for(int i=N-2;i>=0;i--) inv[i]=inv[i+1]*(i+1)%mod;
}
 
ll C(ll a,ll b)
{
    return fac[a]*inv[b]%mod*inv[a-b]%mod;
}
int main()
{
    init();
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin>>n>>m>>k;
    cout<<((C(n*m,k)*C(k,2)%mod)*((n+m)*qpow(3,mod-2)%mod))%mod<<endl;
    return 0;
}