遗传算法简介

今天来讲遗传算法，遗传算法有很多应用，比如寻路问题，八数码问题，囚犯困境问题，动作控制，TSP问题，生产

调度问题，在一个多边形中寻找一个包含在该多边形内的一个圆，函数求最值问题等等。之前讲的模拟退火算法是用

来求解最优化问题的，链接为：http://blog.csdn.net/acdreamers/article/details/10019849 模拟退

火算法用一句话概括就是：贪心过程中引入了随机因素，以一定概率接受一个比当前要差的解，并且这个概率随着时

间的推移而逐渐降低。而今天讲述的遗传算法是模拟生物在自然界物竞天择的生物进化过程，通过维护一个潜在解的

群体执行了多方向的搜索，并支持这些方向上的信息构成和交换。以面为单位的搜索，比以点为单位的搜索，更能发

现全局最优解。

 

Contents

 

    1. 遗传算法的简介

    2. 基因编码方式

    3. 适应评分及选择函数

    4. 基因重组与基因突变

    5. GALib的介绍

    6. 其它GA工具介绍

 

 

1. 遗传算法的简介

 

   说到遗传算法，不得不说网上一个比较贴切的比喻。从前有一群袋鼠，被零散地遗弃于喜马拉雅山脉，于是

   开始在那里艰苦地生活，而海拔低的地方弥漫着一种毒气，所以海拔越低的个体越先死亡，同时袋鼠也会生

   儿育女，经过若干年后，生存能力强的袋鼠最终会越来越往上爬，可能会聚集到很多个山峰上。而又过了若

   干年，可能那些低一点的山峰上的袋鼠都死亡，而最终位于珠穆朗玛峰上的袋鼠生存了下来，从而也就是求

   得了最值。

 

   上面就是遗传算法的核心思想，那么有几个问题要解决。

 

   （1）在遗传算法搜索之前，需要产生一个种群，这个种群是怎么产生的 ？

   （2）种群产生后，又是怎样模拟生物进化得到优良的个体，以及如何评价优良个体 ？

  

   对于问题（1），在遗传算法中，不能直接处理问题空间，需要将问题空间映射到遗传空间，把个体表示成

   由基因按照一定结构组成的染色体，这一转换操作叫做染色体编码。每个个体进行染色体编码后就产生了种

   群。对于问题（2），遗传操作对种群中的个体按其对环境的适应度施加一定的操作，从而实现优胜劣汰的

   进化过程，遗传操作包括选择，交叉和变异。在遗传空间中，个体的迁移由交叉和变异决定的，交叉操作为

   GA提供了一种粗粒，大步伐的搜索手段。变异属于GA的辅助性操作，其主要目的是维持解空间的多样性。通

   过交叉和变异后产生出新个体，然后进行选择，淘汰低劣个体。

 

 

2. 基因编码方式

 

   遗传算法的第一步就是将问题的空间映射到遗传空间，这一步叫做染色体编码。常用的编码方式有二进制编

   码和浮点数编码。

 

  （1）二进制编码

 

      一定精度的二进制编码只能表示一定精度的浮点数，比如我们要求精确到6位小数，而区间为[-1, 2]，

      为了保证精度要求，至少应该将区间划分为等分，因为

 

     

 

      所以编码的二进制串需要22位，把一个二进制串转化为区间[-1, 2]内的一个实数通过如下方法

 

      先将二进制数转化为十进制数，比如得到的十进制数为，那么最终对应[-1, 2]区间内的浮点数为

 

     

 

      这样将一个二进制串对应到一个浮点数，反过来，也可以将一个浮点数映射为一个二进制串。

 

   

  （2）浮点数编码

 

      为了改善遗传算法的复杂性，提高运算速度，提出了浮点数编码。

 

 

3. 适应评分及选择函数

 

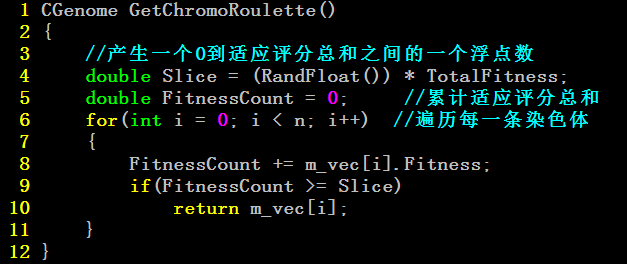
   适应评分函数就是用来衡量哪个个体应该被淘汰，一般来说，取值越差的个体应该被淘汰。适应评分函数

   是物择。而选择函数是天择，从自然界来说，越适应环境的个体越有可能繁殖后代，但是也不能说越适应

   环境的后代就越多，只是从概率上来说是这样。那么怎么建立这种概率关系呢 ？ 一种常用的方法就是轮

   盘赌选择法。 假设种群数为，某个个体的适应度为，那么个体被选中的概率为

  

                           

 

   所以遗传算法中的自然选择过程就是先用适应评分函数计算出各个体的适应评分值，然后再利用轮盘赌选

   择法计算各个体的选择概率，概率越大的被选中的机会也越大。核心代码如下

 

  

 

   上述代码就是选择需要淘汰的个体，体现了生物种群的自然选择的过程。

 

 

4. 基因重组和基因突变

 

   在遗传算法中，每一个个体是用一条染色体来代表的，而染色体之间可能发生交叉，单条染色体也可能发生

   基因突变。重组和突变的目的就是使得子代不同于父代，当然子代不一定就优于父代，只有经过选择后才有

   很大可能性优于父代。二进制编码和浮点数编码都可以进行基因重组，如图

 

  

 

   而基因突变是染色体上某一个位点基因的改变，基因突变使一个基因变成它的等位基因，通常会引起一定的

   表现型变化。代码大致如下

 

  

 

 

5. GALib的介绍

 

   上面基本讲述了遗传算法的原理，接下来就来学习遗传算法是如何解决一些常见应用问题的。主要介绍一个

   遗传算法库---GALib。GALib是美国麻省理工学院Matthew Wall用C++开发的一套遗传算法类库，设计

   非常合理，功能强大而且易于扩展。

 

   GALib提供了三种基本遗传算法：标准型，稳态型和增量型。它们的区别是进化生成的新个体替换父代群体

   的方式。GALib的下载网站为：http://lancet.mit.edu/ga/dist/ 具体用法可以参考example例子。

 

   这个C++库比较强大，以后尽量用这个来实现遗传算法。这里还有一个C++的遗传算法库

 

   链接：https://github.com/kataklinger/Genetic-Algorithms-Library

 

  

6. 其它GA工具介绍

 

   R语言实现的遗传算法

 

   R语言的遗传算法包挺多的，具体可以参考：http://www.tuicool.com/articles/aaQB7nQ

 

   举个例子，以安装mcga包为例，首先进行安装，如下图

 

  

 

   检验一下，如下图

 

  

 

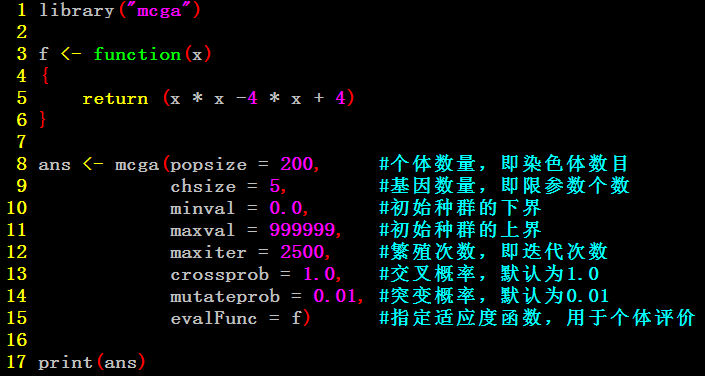
   mcga主要用于求多元函数的最值问题的（最小值）。实例如下

 

  

  

 

   Julia实现遗传算法

 

   在Julia中有一个遗传算法库，叫做GeneticAlgorithms。源代码如下

 

   源码：https://github.com/forio/GeneticAlgorithms.jl

 

   先进行安装，如下

 

   

 

   关于GeneticAlgorithms的使用可以参考例子即可。