POJ 3687 Labeling Balls

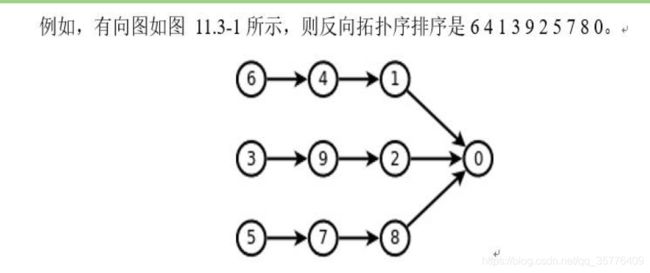
反向拓扑排序

反向拓扑排序
• 所谓反向拓扑排序，就是在拓扑排序的基础上，再增加了一个要
求：
• 条件1：编号最小的节点要尽量排在前面；（也就是首先保证答案序列在所有序列中编号为1 的 节点在所有序列中的位置是最靠前的）
• 条件2：在满足条件1的基础上，编号第二小的节点要尽量排在前面；
• 条件3：在满足条件1和条件2的基础上，编号第三小的节点要尽量排在前
面；
• ……
• 依此类推。

比如上图，好好理解为什么第一个输出的节点不是3 二是6

Labeling Balls

Time Limit: 1000MS Memory Limit: 65536K
Total Submissions: 17971 Accepted: 5213
Description

Windy has N balls of distinct weights from 1 unit to N units. Now he tries to label them with 1 to N in such a way that:

No two balls share the same label.
The labeling satisfies several constrains like “The ball labeled with a is lighter than the one labeled with b”.
Can you help windy to find a solution?

Input

The first line of input is the number of test case. The first line of each test case contains two integers, N (1 ≤ N ≤ 200) and M (0 ≤ M ≤ 40,000). The next M line each contain two integers a and b indicating the ball labeled with a must be lighter than the one labeled with b. (1 ≤ a, b ≤ N) There is a blank line before each test case.

Output

For each test case output on a single line the balls’ weights from label 1 to label N. If several solutions exist, you should output the one with the smallest weight for label 1, then with the smallest weight for label 2, then with the smallest weight for label 3 and so on… If no solution exists, output -1 instead.

Sample Input

5

4 0

4 1
1 1

4 2
1 2
2 1

4 1
2 1

4 1
3 2
Sample Output

1 2 3 4
-1
-1
2 1 3 4
1 3 2 4

声明： 一下内容引自吴永辉老师的课件

简述题意：本题给出N个球，这些球的标记分别从1到N中的某个 数字，它们的重量也分别是从1到N中的某个数字，任意两个球的
标记不同，重量也不相等。本题还给出一些有序对a b，表示标 记a的球比标记b的球轻。本题要求给出符合约束条件的各个球的
重量；若答案有多种，则答案必须让标记为1的球重量尽量轻， 接着是标记为2的球重量尽量轻，一直到标记为N的球尽量轻。 •
本题的原命题是“标记小的球重量尽量轻”，其等价的逆否命题 是“重量大的球标记尽量大”。 设有4个球，约束为4 1和2
3。如果采取正向拓扑排序，编号小的 球先出队，重量从小的开始赋值，则出队的顺序是2 3 4 1，那么 球的重量为w[2] = 1，w[3]
= 2，w[4] = 3，w[1] = 4，这样的结果为 4 1 2 3。但如果采取反向拓扑排序，编号大的球先出队，重量也 从大的开始赋值，则出队的顺序是3 2 1 4，那么球的重量为w[3] = 4，w[2] = 3，w[1] = 2，w[4] =
1，这样的结果为2 3 4 1。 由此可见，如果采用正向拓扑排序，就会把小的重量先赋值，可
能就会导致把小重量赋值给了编号大的球上，而后面编号小的球 却赋了一个比较大的重量，结果不一定使得字典序最小。但是，
如果采用反向拓扑排序，每次编号大的球先出队，重量从大的开 始赋，所产生的字典序最小。

总结：一般情况下 当题目要求最小的编号尽量靠前时，这时候就要考虑建反边了

#include 
#include 
#include 
#include 
using namespace std;
const int Maxn = 251;
int n,m,cnt;
bool map[Maxn][Maxn];
int in[Maxn],head[Maxn],a[Maxn];

struct Node {
    int to,nxt;
}e[Maxn * Maxn];
inline void Add_Edge(int u,int v) {
    e[cnt].to = v; e[cnt].nxt = head[u]; head[u] = cnt++;
}

void Topsort() {
    int k = n;
    priority_queue<int> q;
    while(!q.empty()) q.pop();

    for(int i=1; i<=n; i++) if(in[i] == 0) q.push(i);
    while(!q.empty()) {
        int u = q.top(); q.pop();
        a[u] = k --;
        for(int i=head[u]; i!=-1; i=e[i].nxt) {
            int v = e[i].to;
            in[v]--;
            if(!in[v]) q.push(v);
        }
    }
    if(k != 0) printf("-1\n");
    else {
        for(int i=1; i<n; i++) printf("%d ",a[i]);
        printf("%d\n",a[n]);
    }
}

int main() {
    int T ; scanf("%d",&T);
    while(T--) {
        memset(map,0,sizeof(map));
        memset(head,-1,sizeof(head));
        memset(a,0,sizeof(a));
        memset(in,0,sizeof(in));
        cnt = 0;
        scanf("%d %d",&n,&m);
        while(m--) {
            int u,v;
            scanf("%d %d",&u,&v);
            if(map[u][v]) continue;
            Add_Edge(v,u);
            map[u][v] = 1;// 反向边
            in[u]++;// 反向边x的入度++
        }
        Topsort();
    }
    return 0;
}