Matlab数学建模(六):全局优化
一、学习目标
(1)了解全局优化算法在数学建模中的重要地位。
(2)以著名的旅行商问题为例,掌握如何使用遗传算法。
(3)以经典的Peaks 问题为例,掌握如何使用模拟退火算法。
二、实例演练
1、全局优化算法在数学建模中的重要地位。
全局优化问题常常在数学建模中出现,历年赛题中, 比较经典的这类问题有灾情巡视、公交车调度、彩票问题、露天矿卡车调度、交巡警服务平台、太阳影子定位等等,由此可见全局优化问题的求解算法在数学建模中的重要性。
2、旅行商问题。
旅行商问题是城市数量有限,且城市间旅行成本已知的优化问题。我们的目标是为销售人员找到一个所有城市的有序集合,使成本最小化。为了解决旅行推销员的问题,我们需要一个城市位置和距离的列表,或成本,在他们之间。我们的推销员正在访问美国的一些城市。文件usborder.mat包含变量x和y中的美国地图,以及变量xx和yy中的相同地图的几何简化版本。
load('usborder.mat','x','y','xx','yy');
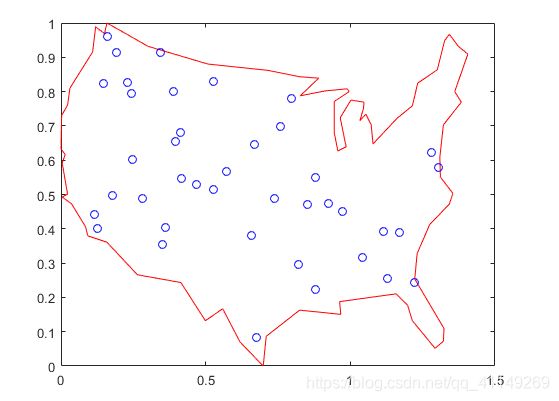
plot(x,y,'Color','red'); hold on;我们将在美国边界内随机生成城市的位置。我们可以使用inpolygon函数来确保所有的城市都在或者非常接近美国边界。
cities = 40;
locations = zeros(cities,2);
n = 1;
while (n <= cities)
xp = rand*1.5;
yp = rand;
if inpolygon(xp,yp,xx,yy)
locations(n,1) = xp;
locations(n,2) = yp;
n = n+1;
end
end
plot(locations(:,1),locations(:,2),'bo');蓝色圆圈代表销售人员需要旅行和运送或提货的城市的位置。给定城市位置列表,我们可以计算出所有城市的距离矩阵。
distances = zeros(cities);
for count1=1:cities,
for count2=1:count1,
x1 = locations(count1,1);
y1 = locations(count1,2);
x2 = locations(count2,1);
y2 = locations(count2,2);
distances(count1,count2)=sqrt((x1-x2)^2+(y1-y2)^2);
distances(count2,count1)=distances(count1,count2);
end;
end;定义目标函数:
FitnessFcn = @(x) traveling_salesman_fitness(x,distances);
my_plot = @(options,state,flag) traveling_salesman_plot(options, ...
state,flag,locations);最后,我们用问题信息调用遗传算法。
numberOfVariables = cities;
[x,fval,reason,output] = ...
ga(FitnessFcn,numberOfVariables,[],[],[],[],[],[],[],options)3、模拟退火算法。
模拟退火(SA)算法也是经典的全局优化算法之一,它脱胎于自然界的物理过程,奇妙地与优化问题挂上了钩。
下面,用模拟退火(SA)算法求解Peaks问题。
1、构建peaks问题。
peaks
problem = createOptimProblem('fmincon',...
'objective',@(x) peaks(x(1),x(2)), ...
'nonlcon',@circularConstraint,...
'x0',[-1 -1],...
'lb',[-3 -3],...
'ub',[3 3],...
'options',optimset('OutputFcn',...
@peaksPlotIterates))2、我们可以先用一般最优算法求解,第3步再用遗传算法求解,形成对比。
[x,f] = fmincon(problem)3、上面那一步是用一般最优算法求解,这次我们尝试一下用模拟退火算法寻找全局最小值。
problem.solver = 'simulannealbnd';
problem.objective = @(x) peaks(x(1),x(2)) + (x(1)^2 + x(2)^2 - 9);
problem.options = saoptimset('OutputFcn',@peaksPlotIterates,...
'Display','iter',...
'InitialTemperature',10,...
'MaxIter',300)
[x,f] = simulannealbnd(problem)