四足机器人 1.稳定性标准
1.1 静态稳定性标准
步行机器人稳定:
如果步行机器人其重心(COG)的水平投影位置在由所有支撑足构成的支撑多边形内部,则步行机器人是静态稳定的。
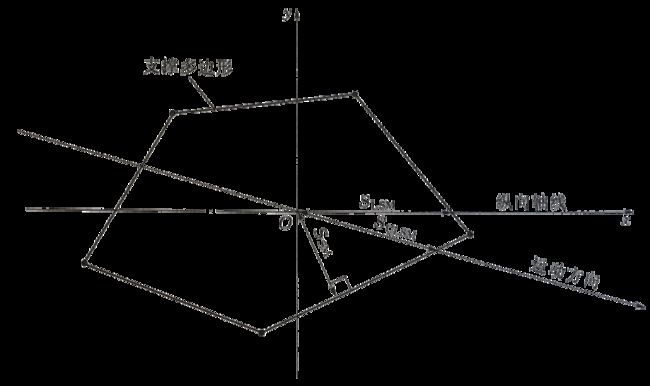
稳定裕度( S S M S_{SM} SSM)(McGhee&Frank)
从COG投影到支撑多边形的最短距离
->稳定裕度短->机器人接近不稳定
纵向稳定裕度( S L S M S_{LSM} SLSM)(Zhang&Song)
在机器人纵轴方向,从COG到支撑多边形边界的最短距离。
考虑到COG高度以及运动学和动力学参数,引入:
能量稳定裕度( S E S M S_{ESM} SESM)(Messuri)
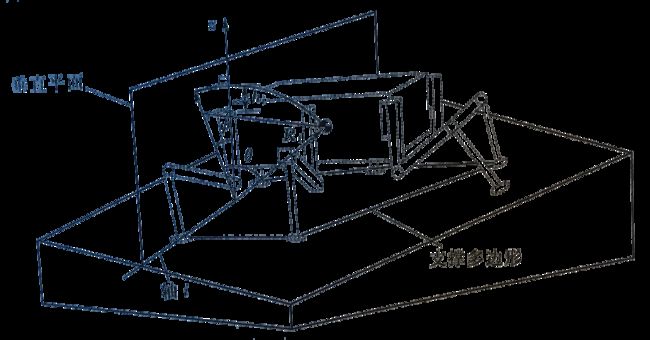
S E S M = m i n ( m g h i ) h i = ∣ R i ∣ ( 1 − c o s θ ) c o s ψ S_{ESM} = min(mgh_i)\\ h_i = |R_i|(1-cos\theta)cos\psi SESM=min(mghi)hi=∣Ri∣(1−cosθ)cosψ
i—支撑多边形作为旋转轴的分段
h i h_i hi—翻滚时COG高度的变化
R i R_i Ri—从COG到旋转轴的矢量
θ \theta θ— R i R_i Ri与垂直平面形成的角度
ψ \psi ψ—相对于水平面旋转的倾斜角
归一化能量稳定裕度( S N E S M S_{NESM} SNESM)(Hirose)
S N E S M = S E S M m g = m i n ( m g h i ) S_{NESM}=\frac{S_{ESM}}{mg}=min(mgh_i) SNESM=mgSESM=min(mghi)
1.2 动态稳定性标准
动态稳定裕度( S Z M P S_{ZMP} SZMP)(Orin)
COP距支撑多边形边缘的最小距离。
压力中心(COP)
对于动态稳定的机器人,作用在COG上的力,沿着COG点合力方向的投影位于支撑多边形内的则稳定
有效质量中心(EMC)为支撑平面上的点,此点处由地面反力引起的力和力矩均为零。
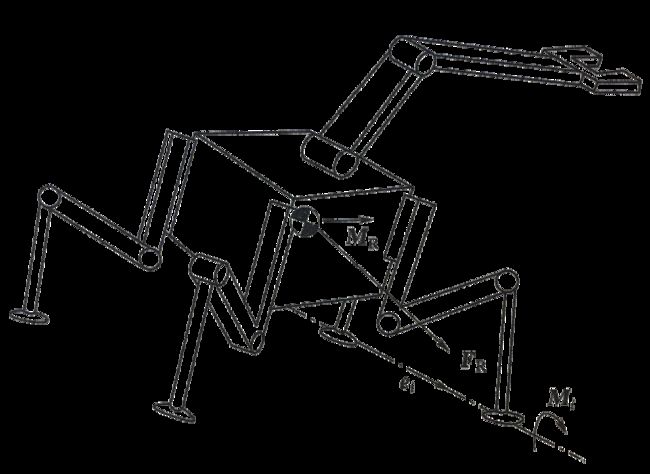
动态稳定裕度( S D S M S_{DSM} SDSM)(Lin&Song)
COG点的动态平衡满足
F I = F S + F G + F M M I = M S + M G + M M F_I = F_S + F_G + F_M\\ M_I = M_S + M_G + M_M FI=FS+FG+FMMI=MS+MG+MM
其中I、S、G、M分别表示惯性、支撑、重力和操纵影响。
S D S M = m i n ( M i m g ) = m i n [ e i ( F R × P i + M R ) m g ] S_{DSM}=min(\frac{M_i}{mg})=min[\frac{e_i(F_R\times P_i+M_R)}{mg}] SDSM=min(mgMi)=min[mgei(FR×Pi+MR)]
其中 P i P_i Pi—从COG到第i支撑足的位置矢量
e i e_i ei—以顺时针方向绕支撑多边形的单位矢量
翻滚稳定裕度( S T S M S_{TSM} STSM)(Yoneda&Hirose)
S T S M = m i n ( ∣ M i ‘ ∣ m g ) S_{TSM} = min(\frac{|M_i^`|}{mg}) STSM=min(mg∣Mi‘∣)
力一角稳定标准 S F A S M S_{FASM} SFASM(Papadopoulos&Rey)
S F A S M = m i n ( α i ) ∣ ∣ F R ∣ ∣ S_{FASM} = min(\alpha_i)||F_R|| SFASM=min(αi)∣∣FR∣∣
归一化动态能量稳定裕度 S N D E S M S_{NDESM} SNDESM(Ghasempoor&Sepehri)
S N D E S M = m i n ( E i ) m g S_{NDESM} = \frac{min(E_i)}{mg} SNDESM=mgmin(Ei)
其中 E i E_i Ei表示支撑多边形的第i侧的稳定性度量,即绕机器人支撑多边形翻滚的第i侧所需的机械能增量
E i = m g ∣ R ∣ ( c o s ϕ − c o s φ ) c o s ψ + ( F R I ⋅ t ) ∣ R ∣ θ + ( M R ⋅ e i ) θ − 1 / 2 I i ω i 2 E_i = mg|R|(cos\phi-cos\varphi)cos\psi+(F_{RI}\cdot t)|R|\theta+(M_R\cdot e_i)\theta-1/2I_i\omega^2_i Ei=mg∣R∣(cosϕ−cosφ)cosψ+(FRI⋅t)∣R∣θ+(MR⋅ei)θ−1/2Iiωi2
R—指向COG位置与支撑多边形的第i侧垂直的正交矢量
F R I F_{RI} FRI—合力的非重力分量/地面作用力 F R F_R FR
I i I_i Ii—绕旋转轴i的惯性力矩
ω i \omega_i ωi—COG的角速度
ψ \psi ψ—支撑多边形的第i侧的倾斜角度
φ \varphi φ—在垂直平面内定位COG所需的旋转角度
ϕ \phi ϕ—COG从垂直平面旋转到临界平面的角度,其中作用在COG全国合力消失
θ \theta θ—两个旋转的相加
1.3 稳定裕度的比较
直接给实验结论了
| 不平坦地形 | 机器人动力 | 操纵动力 | S S M S_{SM} SSM | S N E S M S_{NESM} SNESM | S D S M S_{DSM} SDSM | S T S M S_{TSM} STSM | S F A S M S_{FASM} SFASM | S Z M P S_{ZMP} SZMP | S N D E S M S_{NDESM} SNDESM |
|---|---|---|---|---|---|---|---|---|---|
| 否 | 否 | 否 | √ \surd √ | * | √ \surd √ | √ \surd √ | * | √ \surd √ | * |
| 否 | 是 | 否 | × \times × | × \times × | √ \surd √ | √ \surd √ | * | √ \surd √ | * |
| 否 | 是 | 是 | × \times × | × \times × | √ \surd √ | √ \surd √ | √ \surd √ | √ \surd √ | * |
| 是 | 否 | 否 | √ \surd √ | * | √ \surd √ | √ \surd √ | √ \surd √ | √ \surd √ | * |
| 是 | 是 | 否 | × \times × | × \times × | √ \surd √ | √ \surd √ | √ \surd √ | √ \surd √ | * |
| 是 | 是 | 是 | × \times × | × \times × | √ \surd √ | √ \surd √ | √ \surd √ | √ \surd √ | * |
稳定裕度分类表 √ \surd √ : 有效 × \times ×: 无效 * : 最合适
| 运算类型 | S S M S_{SM} SSM | S N E S M S_{NESM} SNESM | S D S M S_{DSM} SDSM | S T S M S_{TSM} STSM | S F A S M S_{FASM} SFASM | S Z M P S_{ZMP} SZMP | S N D E S M S_{NDESM} SNDESM |
|---|---|---|---|---|---|---|---|
| 加法 | 17n | 33n | 44n | 86n | 109n | 67n | 60n |
| 乘积 | 13n | 23n | 39n | 90n | 117n | 70n | 57n |
| 三角函数 | — | — | — | — | 3n | — | 3n |
| 平方根 | n | 2n | 2n | 3n | 6n | 2n | 3n |
现有稳定性标准的计算复杂度
1.4 总结
S S M S_{SM} SSM和 S N E S M S_{NESM} SNESM仅适用于无动力, S N E S M S_{NESM} SNESM最优
S N D E S M S_{NDESM} SNDESM适合最广且优