【数学建模】最优化模型
文章目录
- A 概述
- 1 最优化模型的一般形式
- 2 最优化模型的分类
- B 优化模型之运输问题
- 1 运输问题的数学模型
- 2 一般运输问题的求解
- C 优化模型之下料问题
- 1 一般下料问题的最优解法
- 2 下料问题的非线性方法
- 3 大型下料问题的解法
- D 优化模型之指派问题
- 1 矩阵覆盖法
- 2 Lingo求解
- E 优化模型之目标规划
- 1 目标规划与线性规划的区别
- 2 目标规划模型
- F 优化模型之装箱问题
- 1 一维装箱问题
- 2 选择装箱问题
- 3 装箱序号提取
- G 优化模型之生产计划问题
- 1 最少变量个数的一般模型
- 2 存储平衡模型
- 3 转化运输模型
- H 优化模型之非线性规划
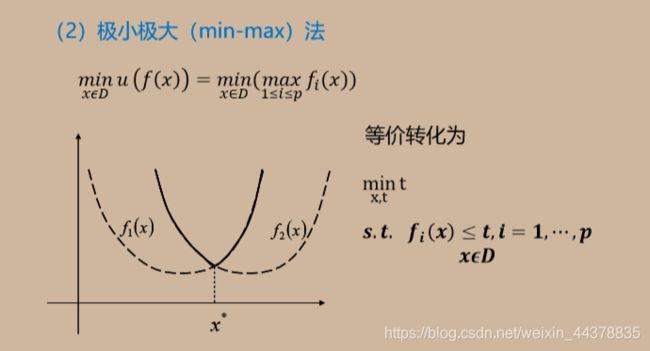
- I 优化模型之多目标规划
- 1 引例
- 2 多目标问题的数学模型
- 3 多目标问题的求解方法
A 概述
1 最优化模型的一般形式
最优化方法是指在一系列客观或主观限制条件下,寻求 合理分配有限资源使所关注的某个或多个指标达到最大(或 最小)的数学理论和方法,是运筹学里一个十分重要的分支。
三个要素:决策变量decision bariable,目标函数 objective function,约束条件constraints。
可行域:满足约束条件的所有x范围。
可行解:可行域上的每一个解称为可行解。
最优解:让目标函数达到最优的解。分为全局最优解和局部最优解:
最优值:最优解对应的目标函数的值
2 最优化模型的分类
B 优化模型之运输问题
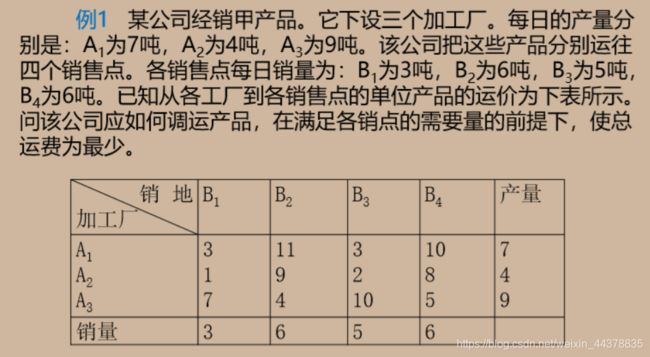
1 运输问题的数学模型
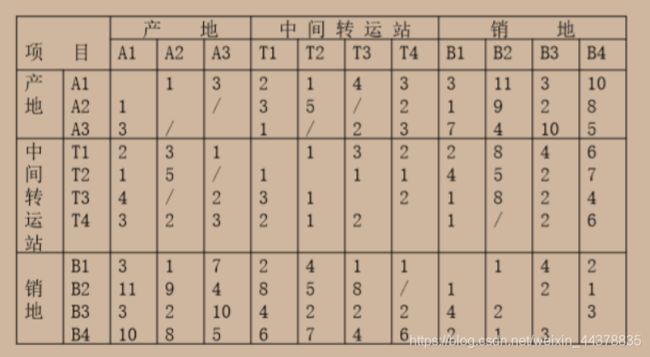
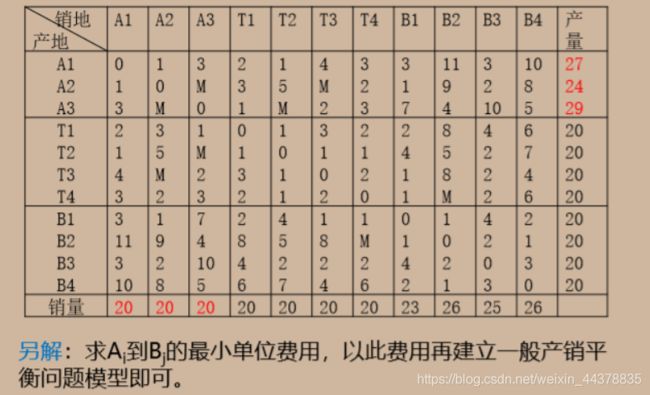
2 一般运输问题的求解
此题为产销平衡问题。
model:
title 运输问题;
sets:
s1/1..3/:a; !定义产地;
s2/1..4/:b; !定义销地;
ss(s1,s2):x,c;!定义运量和单价;
endsets
data:
c=3 11 3 10
1 9 2 8
7 4 10 5; !单价;
a=7,4,9; ! 产地限量;
b=3,6,5,6; ! 销地需求量;
enddata
min=@sum(ss(i,j):c(i,j)*x(i,j));
@for(s1(i):@sum(s2(j):x(i,j))<a(i)); ! 产地上限;
@for(s2(j):@sum(s1(i):x(i,j))>b(j)); ! 销地下限;
end
运往仓库的量小于产量;
仓库输入等于输出;
仓库输出等于需求量;
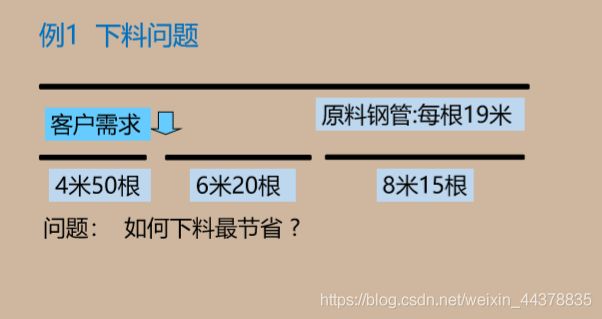
C 优化模型之下料问题
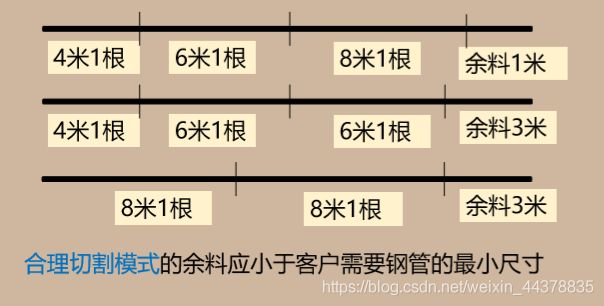
1 一般下料问题的最优解法
model:
sets:
s/1..7/:x;
endsets
Min=3*x(1)+x(2)+3*x(3)+3*x(4)+x(5)+x(6)+3*x(7);
4*x(1)+3*x(2)+2*x(3)+x(4)+x(5)>50;
x(2)+2*x(4)+x(5)+3*x(6)> 20;
x(3)+x(5)+2*x(7)>15;
@for(s(i):@gin(x(i)));
end
2 下料问题的非线性方法
3 大型下料问题的解法
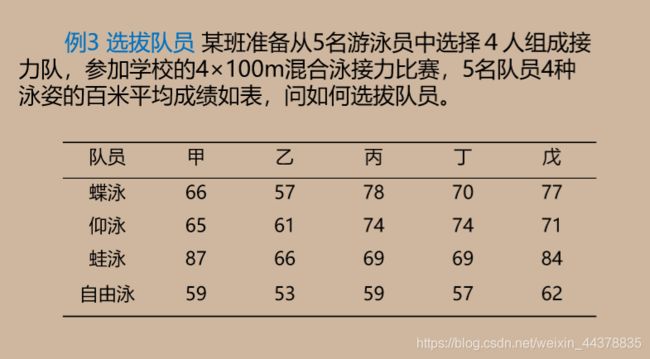
D 优化模型之指派问题
1 矩阵覆盖法
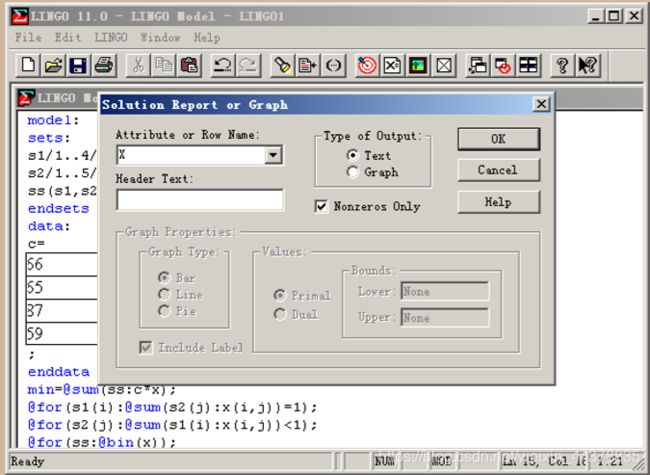
2 Lingo求解
model:
sets:
s1/1..4/:;
s2/1..5/:;
ss(s1,s2):c,x;
endsets
data:
c=
66 57 78 70 77
65 61 74 64 71
87 66 69 69 84
59 53 59 57 62;
enddata
min=@sum(ss:c*x);
@for(s1(i):@sum(s2(j):x(i,j))=1);
@for(s2(j):@sum(s1(i):x(i,j))<1);
@for(ss:@bin(x));
end
E 优化模型之目标规划
1 目标规划与线性规划的区别
2 目标规划模型
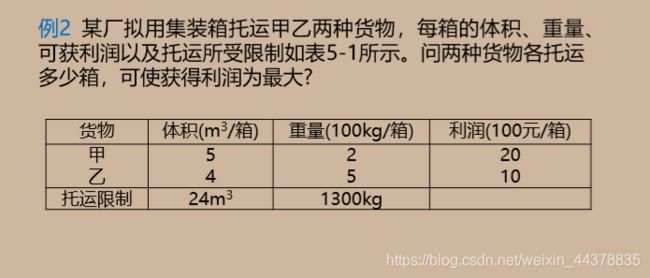
F 优化模型之装箱问题
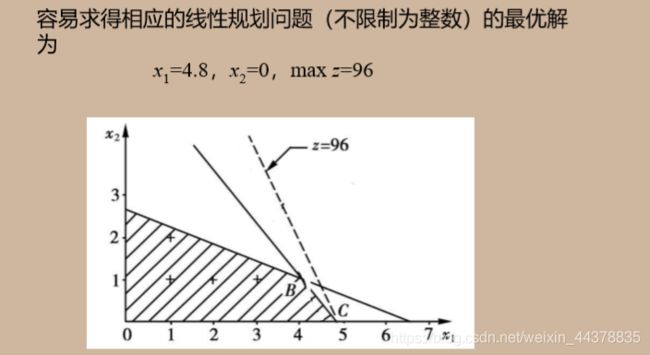
1 一维装箱问题
2 选择装箱问题
3 装箱序号提取
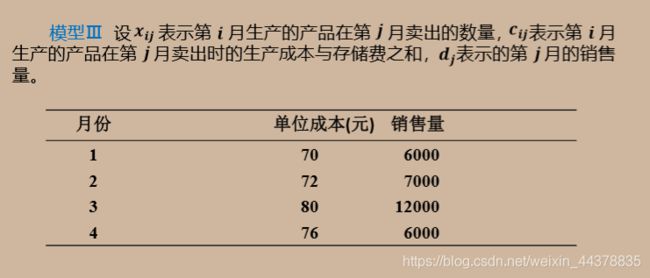
G 优化模型之生产计划问题
1 最少变量个数的一般模型
model:
sets:
yuefen/1..4/:c,x,e,d;
endsets
data:
c=70,71,80,76;
d=6000,7000,12000,6000;
e=2,2,2,2;
a=10000;
enddata
min=@sum(yuefen:c*x)+@sum(yuefen(j)|j#lt#4:@sum(yuefen(i)|i#le#j:(x-d))*e(j+1));
@for(yuefen(j)|j#lt#4:@sum(yuefen(i)|i#le#j:x)>@sum(yuefen(i)|i#le#j:d));
@sum(yuefen:x)=@sum(yuefen:d);
@for(yuefen:x2 存储平衡模型
model:
sets:
yuefen/1..4/:c,x,e,d,s;
endsets
data:
c=70,71,80,76;
d=6000,7000,12000,6000;
e=2,2,2,2;
a=10000;
enddata
min=@sum(yuefen:c*x+e*s);
@for(yuefen(i)|i#lt#4:s(i+1)=s(i)+x(i)-d(i));
s(4)+x(4)-d(4)=0;
@for(yuefen:x3 转化运输模型
model:
sets:
yuefen/1..4/:a,d,xx;
link(yuefen,yuefen)|&2#ge#&1:c,x;
endsets
data:
c=70 72 74 76
71 73 75
80 82
76;
d=6000 7000 12000 6000;
a=10000 10000 10000 10000;
enddata
min=@sum(link:c*x);
@for(yuefen(i): @sum(yuefen(j)|j#ge#i: x(i,j))d(j););
@for(yuefen(i): xx=@sum(yuefen(j)|j#ge#i: x(i,j)));
end
H 优化模型之非线性规划
MODEL:
Title 第二小问;
sets:
demand/1..6/:a,b,d;
supply/1..2/:x,y,e;
link(supply,demand):c;
endsets
data:
a=1.25,8.75,0.5,5.75,3,7.25;
b=1.25,0.75,4.75,5,6.5,7.75;
d=3,5,4,7,6,11; e=20,20;
enddata
!初始段:对集合属性定义初值(迭代算法的迭代初值);
init:
!初始点;
x,y=5,1,2,7;
endinit
min=@sum(link(i,j): c(i,j)*((x(i)-a(j))^2+(y(i)-b(j))^2)^(1/2) );
@for(demand(j):@sum(supply(i):c(i,j)) =d(j););
@for(supply(i): @sum(demand(j):c(i,j)) <=e(i); );
@for(supply: @bnd(0.5,X,8.75);
@bnd(0.75,Y,7.75); );
end