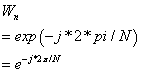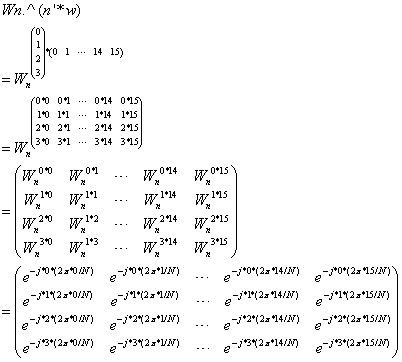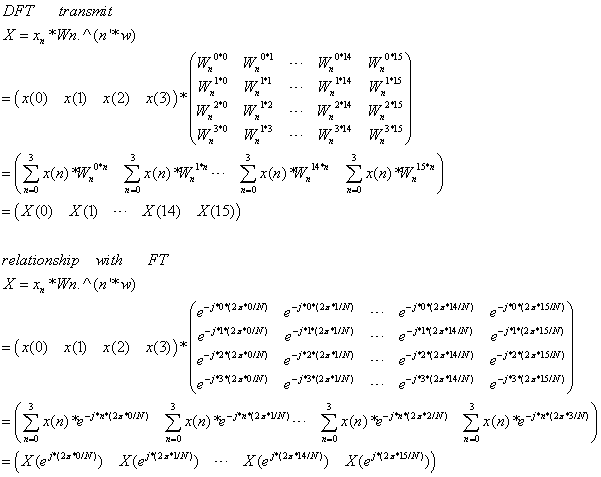离散傅里叶变换（DFT）

目录 

    一、研究的意义

    二、DFT的定义

    三、DFT与傅里叶变换和Z变换的关系

    四、DFT的周期性

    五、matlab实验

        五.1 程序   

           五.2 实验结果

一、研究的意义

    DTFT计算公式，中的w取值是连续的而且从负无穷大到正无穷大，对于计算机处理是不可能的，需要无限细分无限区间。即使在DTFT小节中用matlab实现计算，也只是将(-pi,pi)区间划分成1600份来逼近DTFT的效果。

    实际上真正用的是DFT，离散傅里叶变换。离散傅里叶变换可以将连续的频谱转化成离散的频谱去计算，这样就易于计算机编程实现傅里叶变换的计算。FFT算法的出现，使得DFT的计算速度更快。

二、DFT的定义

    由上边的定义可知，w=(2*pi/N)*k ,k=0,1,......,N-1，所以w的范围为[0，(N-1/N)*2*pi]。因为是离散取值，实际的区间长度为N，但不含第N个点，w的范围就是[0，2*pi)。

    也就是说DFT变换的频谱范围是在竖轴的右侧（>0），而且取了FT变换的一个周期(0,2*pi)。

三、DFT与傅里叶变换和Z变换的关系

四、DFT的周期性

    以下的四个式子，在程序设计和理解程序中经常用到，wd、wa分别为数字角频率和其对应的模拟角频率。

（1），描述了模拟角频率、数字角频率以及DFT变换的k之间的对应关系

（2），描述了数字角频率与模拟角频率之间的关系

（3），描述了数字角频率和DFT变换的k之间的关系

（4），描述了模拟角频率和DFT变换的k之间的关系

五、matlab实验

1、程序     

 1 M=4;                         %原离散信号有4点
 2 n=[0:1:M-1];                 %原信号是1行4列的矩阵
 3 xn=[1 1 1 1];                %构建原始信号 
 4 subplot(3,1,1);
 5 stem(n,xn);                  %画图
 6 title('原始信号');
 7 
 8 N=16;                        %16点DFT变换
 9 k=[0:1:N-1];                 %k取值为0,1,2，···，15
10 Wn=exp(-j*2*pi/N);           %求Wn
11 X=xn*(Wn.^(n'*k));           %求DFT变换，原始定义的方法，对复指数分量求和而得
12 subplot(3,1,2);
13 stem(k,abs(X));
14 title('原信号的16点DFT变换');
15 
16 N1=8;                        %8点DFT变换
17 k1=[0:1:N1-1];               %k取值为0,1,2，···，7  
18 Wn1=exp(-j*2*pi/N1);         %求Wn1
19 X1=xn*(Wn1.^(n'*k1));        %求DFT变换，采用原始定义的方法，对复指数分量求和而得
20 subplot(3,1,3);
21 stem(k1,abs(X1));
22 title('原信号的8点DFT变换');

 说明：

（1）DFT的计算利用的是定义法

（2）程序第10行

       程序第11行计算过程

 

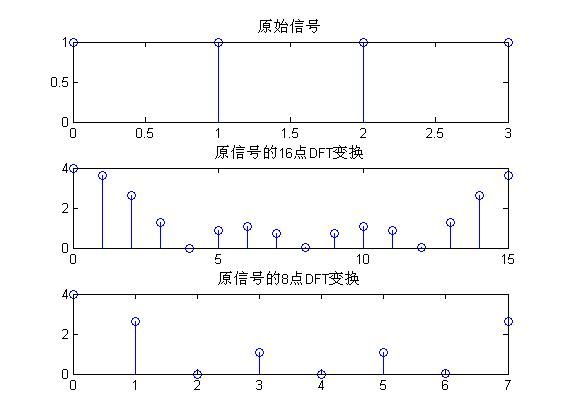
2、实验结果

 

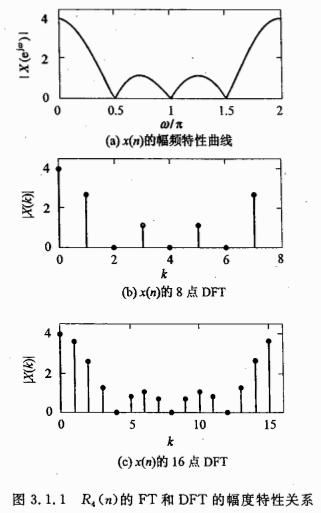
 说明：上图结果证明了离散傅里叶变化是对FT变化在区间（0,2*pi）的等间距N点采样。

 

参考：西电《数字信号处理》第三版   

        用matlab对信号进行傅里叶变换