幅度调制后的频率混叠

人类在实践无线通信的过程中使用信号高频调制的方式来将传递的信号的频谱搬移到高频，通过天线完成电磁波的发送与接受。这种信号调制方式作为信号频谱分析的应用，也称为信号与系统课程中的重要内容。

^{▲ 无线通讯方式及其天线}

本文对信号幅度调制和解调进行讨论。通过公式、波形、频谱分析对幅度调制中的混叠现象进行描述。

 

幅度调制

信号调制中，幅度调制形式简单，应用广泛。在形式可以描述成信号$f\left(t\right)$与载波信号$\cos \left({\omega }_{c}t\right)$的乘积关系。在实际工程中，载波信号的频率${\omega }_c$通常远大于信号$f\left(t\right)$的最高频率。后期通过同步解调方式，可以从调制信号中恢复出原来的信号。

下面公式描述了幅度调制（载波抑制调幅）的过程：

$$y\left(t\right)=f\left(t\right)\cdot \cos \left({\omega }_{c}t+\theta \right)$$

实现的系统框图显示如下：

^{▲ 信号幅度调制的系统框图}

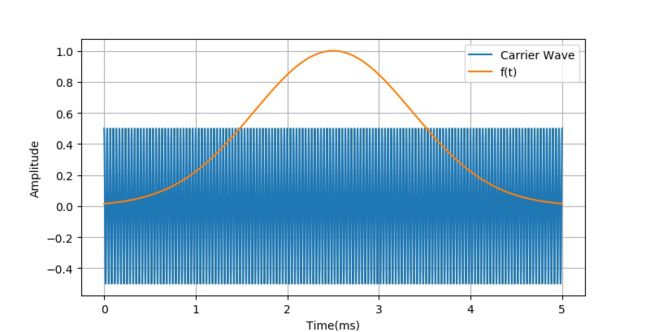
下面通过波形显示了幅度正弦调制的过程。其中信号$f\left(t\right)$的频率为1kHz，载波的频率为30kHz。这样选择只是为了能够从波形上还可以看出两个信号的波形。实际中往往载波的频谱${\omega }_c$比调制信号$f\left(t\right)$的频率高出两三个数量级以上。

$$f\left(t\right)=\cos \left(2\pi \cdot 1000\cdot t\right)$$$$f_c\left(t\right)=0.5\cdot \cos \left(2\pi \cdot 30\cdot 10^3\cdot t\right)$$

^{▲ 载波信号与低频调制信号}

下图显示了信号$f\left(t\right)$与载波信号$\cos \left({\omega }_{c}t\right)$相乘之后的调幅波形。

^{▲ 幅度调制信号}

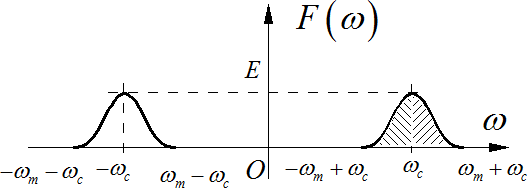
幅度调制后的信号频谱是原来信号的频谱分别左右搬移到载波频率附近的位置，形成高频信号。下面显示了前面正弦信号调制后的频谱。

^{▲ 载波抑制幅度调制信号的频谱示意图}

下面再通过对高斯信号调制后的信号波形：
$$f\left(t\right)=e^{-\frac{{\left(t-2.5\right)}^2}{1.5}}$$$$f_c\left(t\right)=0.5\cdot \cos \left(2\pi \cdot 30\cdot 10^3\cdot t\right)$$

^{▲ 调制信号与载波信号}

高斯信号调幅后的波形如下图所示。它对应的频谱与前面正弦波调制后的频谱相比只是将原来的一对冲激频谱改成了高斯信号频谱。这是由于高斯信号的傅里叶变换也是高斯信号。

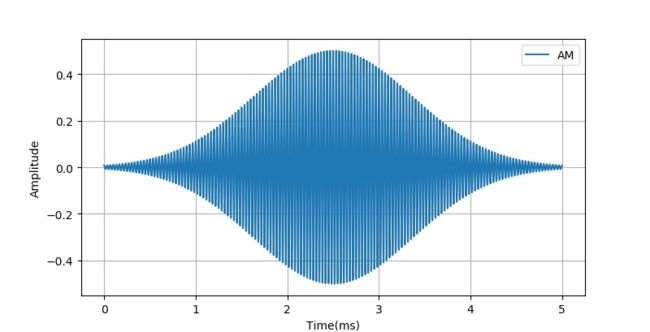
^{▲ 高斯信号调制后的波形}

^{▲ 高斯信号调制信号频谱示意图}

 

同步解调

相比与普通调幅信号，这种载波抑制的调幅需要使用同步检波的方式来解调。具体过程通过数学描述如下：

$$w\left(t\right)=y\left(t\right)\cdot \cos {\omega }_{c}t=f\left(t\right)\cdot {\cos }^2\left(t\right)$$$$=f\left(t\right)\left[\frac{1}{2}+\frac{1}{2}\cos 2{\omega }_{c}t\right]$$$$=\frac{1}{2}f\left(t\right)+\frac{1}{2}f\left(t\right)\cdot \cos 2{\omega }_{c}t$$

将调幅波形再乘以载波信号，相当于再幅度调制。在生成信号中包括两个成分，一个是信号本身$\frac{1}{2}f\left(t\right)$，幅度降低了一半；另一个是信号与两倍的载频波形的乘积。后面再通过一个低通滤波器便可以将调制信号$f\left(t\right)$进行恢复。

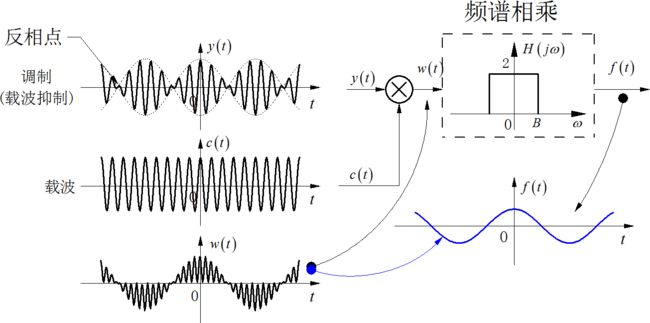
下图显示了同步解调的过程 以及各部分的波形。

^{▲ 同步解调的过程波形图}

对于前面给出的实验波形，下面绘制出了信号乘以载波之后的波形。可以看出，其中的低频分量就是被调制的信号。

^{▲ 调幅信号乘以载波信号以及其中的低频信号}

^{▲ 高斯信号同步解调后的波形}

 

频率混叠

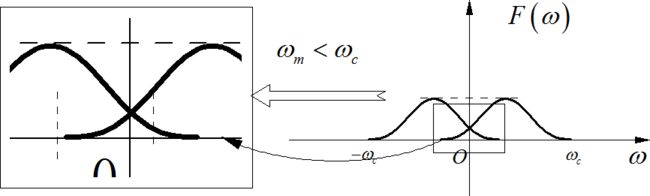
在前面讲述信号的幅度调制与解调过程中，都是假设信号的频谱远远小于载波的频率。这样信号被调制后，它的频谱搬移到高频时，左右的频谱之间没有重叠。但是如果调制频谱低，小于信号中最高频率，那么调制后的信号频谱中，左右两个搬移后的频谱之间就会有混叠。这就为后面进行信号恢复埋下了隐患。

下面将前面实验中载波的频率从原来的30kHz，降低到0.5kHz，给出对应的调制波形。

$$f\left(t\right)=e^{-\frac{{\left(t-2.5\right)}^2}{1.5}}$$$$f_c\left(t\right)=\cos \left(2\pi \cdot 0.5\cdot 10^{3}t\right)$$

^{▲ 高斯信号与低频的载波信号}

^{▲ 高斯信号低频调幅后的波形}

同样使用同步解调，所得到的信号中，信号本身$\frac{1}{2}f\left(t\right)$与两倍频调制的信号$\frac{1}{2}f\left(t\right)\cdot \cos \left(2{\omega }_{c}t\right)$之间频谱也同样存在着混叠，这样就会使得低通滤波器无法将信号本身恢复出来了。

下图显示了上面调幅信号与载波信号相乘之后的结果（蓝色的AM曲线），对比原来的高斯信号（橙色Low Frequency曲线），可以看出使用普通的低通滤波器很难从蓝色曲线恢复出橙色曲线了。

^{▲ 调幅信号与载波信号乘积之后的信号}

^{▲ 高斯调制信号频谱混叠示意图}

 

复震荡信号调制

为了避免幅度调制后的频率混叠带来信号恢复的困难，在实践中，可以采用复震荡信号调制的方式。也就是将原来的信号调制在一对相位相差90°（正交）的载波信号上，形成一对正交调制信号。在数学上，可以将这对信号看成复数的实部和虚部，所组成的复值信号的频谱则是原来信号的频谱往右平移，自然就没有了混叠的问题。

^{▲ 复震荡信号调制框图}

下面公式表示复指数震荡信号的调制的过程：
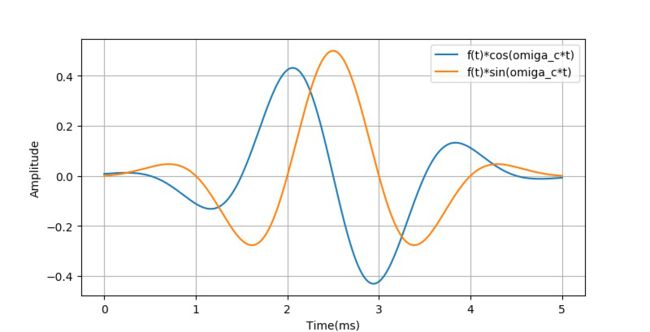
$$f\left(t\right).e^{j{\omega }_{c}t}=f\left(t\right)\cdot \cos \left({\omega }_{c}t\right)+j\cdot f\left(t\right)\cdot \sin \left({\omega }_{c}t\right)$$

下图显示了上面复指数调制后的实部、虚部两路信号波形。

^{▲ 复指数调制后的两路波形}

如果需要恢复出原来的信号，则将原来的信号乘以前面复震荡信号的共轭信号$e^{-j\left({\omega }_{c}t+\phi \right)}$，所生成信号的实部就是恢复的原来信号了。

根据复数的乘法运算，复数乘积的实部等于原来两个复数的实部相乘，减去虚部相乘的结果。
$$\left(x+j\cdot y\right)\cdot \left(w+j\cdot z\right)=\left(x\cdot w-y\cdot z\right)+j\left(w\cdot y+x\cdot z\right)$$

因此对应的复指数震荡信号同步解调过程就是：
$$\left[f\left(t\right)\cos \left({\omega }_{c}t\right)+j\cdot f\left(t\right)\sin \left({\omega }_{c}t\right)\right]\cdot \left[\cos \left({\omega }_{c}t\right)-j\cdot \sin \left({\omega }_{c}t\right)\right]$$$$=f\left(t\right)\left[{\cos }^2\left({\omega }_{c}t\right)+{\sin }^2\left({\omega }_{c}t\right)\right]=f\left(t\right)$$

下图显示了使用复指数调制后的实部和虚部分别与$\cos \left({\omega }_{c}t\right),\sin \left({\omega }_{c}t\right)$相乘之后的波形（蓝色，橙色），他们相加之后的波形（绿色）就是回复后的高斯波形。

^{▲ 进行复指数回复后的波形}

如果信号$f\left(t\right)$的幅值始终大于零0，即$f\left(t\right)\ge 0$，那么从复震荡调制信号恢复原来信号还可以简单的通过求复调制信号的幅度来恢复：

$$\left|f\left(t\right)\cdot \cos \left({\omega }_{c}t\right)+j\cdot f\left(t\right)\cdot \sin \left({\omega }_{c}t\right)\right|=\left|f\left(t\right)\right|=f\left(t\right)$$