图论 —— 二分图 —— 匈牙利算法
【基本概念】
1.交替路
从一个未匹配点出发,依次经过 非匹配边、匹配边、非匹配边… 形成的路径
2.增广路
定义:设 M 为二分图 G 已匹配边的集合,若 P 是图 G 中一条连通两个未匹配点的路径(起点在 X/Y 部,终点在 Y/X 部),且属 M 的边(匹配边)与不属 M 的边(非匹配边)在 P 上交替出现,则称 P 为相对 M 的一条增广路径。
由于增广路的第一条边是没有参与匹配的,第二条边参与了匹配,...,最后一条边没有参与匹配,并且起点和终点还没有被选择过,显然 P 有奇数条边。
简单来说,从一个未匹配点出发,走交替路,若途径另一未匹配点(除起点外),则这条交替路称为增广路。
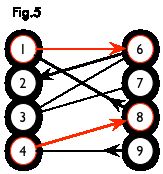
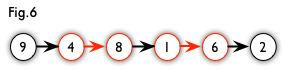
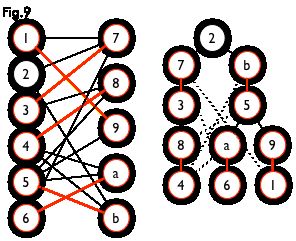
如下图,左图中的一条增广路如右图所示,图中的匹配点均用红色标出
3.增广路性质
- P 的长度必为奇数,第一条边和最后一条边都不属于 M,且两个端点分属两个集合,均未匹配。
- P 的非匹配边比匹配边多一条。
- P 经过取反操作可以得到一个更大的匹配 M’。
- M 为 G 的最大匹配当且仅当不存在相对于 M 的增广路径。
4.增广路定理
由于增广路中间的匹配节点不存在其他相连的匹配边,因此交换增广路中的匹配边与非匹配边不会破坏匹配的性质。
由增广路性质可知,只要把增广路中的匹配边和非匹配边交换,交换后,图中的匹配边数目比原来多了 1 条。
故而,可以通过不停地找增广路来增加匹配中的匹配边和匹配点,找不到增广路时,即达到最大匹配,这就是增广路定理。
5.匈牙利树
匈牙利树一般由 DFS 构造(类似于 DFS 树),其是从一个未匹配点出发进行 DFS(必须走交替路),直到不能再扩展为止。
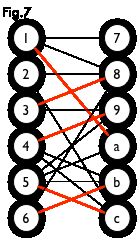
如下图,通过左侧的二分图,进行 DFS 可以得到右侧的树,但这棵树存在一叶结点为非匹配点(7号),而匈牙利树要求所有叶结点均为匹配点,故这棵树不是匈牙利树。
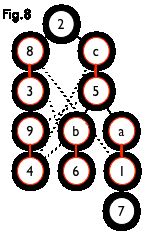
但若原图中不含 7 号结点,那么从 2 号结点出发就会得到一棵匈牙利树,如下图
【匈牙利算法流程】
匈牙利算法是用增广路来求最大匹配的算法,在求最大匹配前,需要先用 DFS 或 BFS 找到增广路。
1.流程
- 从左边第 1 个点开始,挑选未匹配点进行搜索,寻找增广路
1)若经过一个未匹配点,则寻找成功,更新路径信息,匹配边数 +1,停止搜索。
2)若一直没有找到增广路,则不再从这个点开始搜索。事实上,此时搜索后会形成一棵匈牙利树。我们可以永久性地把它从图中删去,而不影响结果。 - 由于找到增广路后需要沿着路径更新匹配,因此需要一个结构来记录路径上的点,DFS 版本通过函数调用隐式地使用一个栈,而 BFS 版本使用 pre 数组(前驱结点)。
2.性能比较
无论是使用 DFS 还是 BFS,两个版本的时间复杂度均为 O(V*E)。
DFS 的优点是思路清晰,代码量少,但性能不如 BFS;BFS 的优点是速度较快,但代码量大
对于稀疏图,BFS 版本明显快于 DFS 版本,对于稠密图,两者不相上下,因而当图为稀疏图时,常选用 DFS 版本,当图为稠密图时,常选用 BFS 版本。
3.koning 定理及推论
1)基本概念
k-正则图:各顶点的度均为 k 的无向简单图
最大匹配数:最大匹配的匹配边的数目
最大独立集数:选取最多的点集,使点集中任意两点均不相连
最小点覆盖数:选取最少的点集,使任意一条边都至少有一个端点在点集中
2)内容
- 最大匹配数 = 最小点覆盖数
- 最大独立集数 = 顶点数 - 最大匹配数
【实现】
1.最大匹配数/最小点覆盖数
DFS 版本
int n,m;//x、y中结点个数,下标从0开始
bool vis[N];//vis[i]表示是否在交替路中
int link[N];//存储连接点
vector G[N];//存边
bool dfs(int x){
for(int i=0;i BFS 版本
int n,m;//左边点数,右边点数
int vis[N];//vis[i]表示是否在交替路中
int link[N];//存连接点
int pre[N];//存前驱结点
vector G[N];//存边
queue Q;
int hungarian(){
memset(vis,-1,sizeof(vis));
memset(pre,-1,sizeof(pre));
memset(link,-1,sizeof(link));
int ans=0;//记录最大匹配数
for(int i=1;i<=n;i++){
if(link[i]==-1){//若点未匹配
pre[i]=-1;//没有前驱
while(!Q.empty())//清空队列
Q.pop();
Q.push(i);
bool flag=false;
while(!Q.empty() && !flag){
int x=Q.front();
for(int j=0;j=0)//在已匹配点中
pre[link[y]]=x;
else {//找到未匹配点,交替路变增广路
flag=true;
int d=x;
int e=y;
while(d!=-1){//找到一个未匹配点,无法构成匈牙利树,让所有点不断的往回更新,重选下一个
int temp=link[d];
link[d]=e;
link[e]=d;
d=pre[d];
e=temp;
}
}
}
}
Q.pop();
}
if(link[i]!=-1)//统计最大匹配数
ans++;
}
}
return ans;
}
int main(){
while(scanf("%d%d",&n,&m)!=EOF){
while(m--){
int x,y;
scanf("%d%d",&x,&y);
G[x].push_back(y);
G[y].push_back(x);
}
printf("%d\n", hungarian());//输出最大匹配数
}
return 0;
}
2.最大独立集
int n,m;
bool vis[N];
int link[N];
bool G[N][N];
bool dfs(int x){
for(int y=1;y<=m;y++){
if(G[x][y]&&!vis[y]){
vis[y]=true;
if(link[y]==-1 || dfs(link[y])){
link[y]=x;
return true;
}
}
}
return false;
}
int hungarian(){
int ans=0;
for(int i=1;i<=n;i++){
memset(vis,false,sizeof(vis));
if(dfs(i))
ans++;
}
return ans;
}
int main(){
while(scanf("%d%d",&n,&m)!=EOF&&(n+m)){
memset(link,-1,sizeof(link));
memset(G,true,sizeof(G));
while(m--){
int x,y;
scanf("%d%d",&x,&y);
G[x][y]=false;//不满足条件则连一条边
}
int mate=hungarian();//最大匹配数
int res=n-mate;//最大独立集
printf("%d\n",res);
}
return 0;
}
3.经典应用——行列拆点建图
1)问题
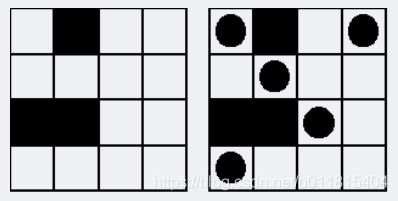
对于一个 n*m 的图," . " 代表空白区域," # " 代表墙,现在要向空白区域内放棋子,要求同一行、同一列只能放一个棋子,除非该行/列上有墙阻隔,问最多能放多少枚棋子
如下图,对于一个 4*4 的图,黑色代表墙,最多能放 5 枚棋子
2)解答
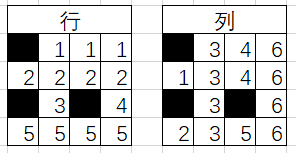
只有在墙的阻隔情况下,才会出现一行/列出现多个点的情况,那么可以考虑进行缩点,将同一行且没有墙体阻隔的区域缩成一个点,放到左点集中,将同一列且没有墙体阻隔的区域缩成一个点,放到右点集中,从而建成一个二分图
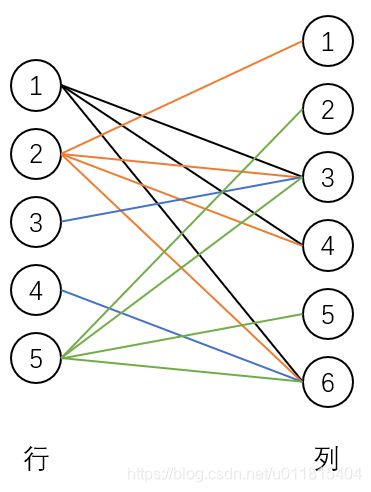
假设 i 为行编号,j 为列编号,若 i-j 之间存在一条边,就相当于在方格 (i,j) 上放了一个点,这个假设使得在没有墙体阻隔的情况下,i 行 j 列不能再放其他的点,那么在不考虑 不能同行同列 的情况下,将所有边连接起来,即行列缩点后,对应方格编号连边
建好图后,在图上求最大匹配即可
3)实现
int n,m;//n行m列
bool vis[N];//vis[i]表示是否在交替路中
int link[N];//存储连接点
int G[N][N];//存边
char str[N][N];
int x[N][N],cntX;//行点集
int y[N][N],cntY;//列点集
bool dfs(int x){
for(int y=0;y