刷题ROSALIND，练编程水平
http://rosalind.info/problems/list-view/

11. Mortal Fibonacci Rabbits (斐波那奇兔子有毒)

image.png

解题思路
- 假设每对兔子在成年阶段每个月能产生1对幼年兔子，每对兔子能存活3个月(繁殖2个月)，问到第n个月共有多少对兔子？

经过月数	0	1	2	3	4	5	6	7	8	9
兔子个数	1	1	2	3	5	8	13	21	34	55
总兔子	1	1	2	2	3	4	5	7	9	12

规律
F0=1,F1=1, F2=2
F3=F1+F2-F0
所以，可以推导出
Fn=Fn-1+Fn-2-Fn-3(n>=3)

def fibRabbits(n,k):
    # 第0，1个月是1
    if n<2:
        return 1
    # 第二个月是2
    elif n==2:
        return 2
    #3个月以上用公式
    else:
        return (fibRabbits(n-1,k)+fibRabbits(n-2,k)-fibRabbits(n-4,k))
print(fibRabbits(9,3))

12. Overlap Graphs(重叠图)

image.png

解题思路
- 第一个序列的末尾3字符==第二个序列的开头3字符

# coding=utf-8

# method1
data = {'Rosalind_0442': 'AAATCCC',
        'Rosalind_0498': 'AAATAAA',
        'Rosalind_2323': 'TTTTCCC',
        'Rosalind_2391': 'AAATTTT',
        'Rosalind_5013': 'GGGTGGG'}


def is_k_overlap(s1, s2, k):
    return s1[-k:] == s2[:k]


import itertools


def k_edges(data, k):
    edges = []
    # data 里面任意取两个比较
    for u, v in itertools.combinations(data, 2):
        u_dna, v_dna = data[u], data[v]
        if is_k_overlap(u_dna, v_dna, k):
            edges.append((u, v))
        if is_k_overlap(v_dna, u_dna, k):
            edges.append((v, u))
    return edges
print(k_edges(data, 3))

[('Rosalind_0498', 'Rosalind_0442'), ('Rosalind_0498', 'Rosalind_2391'), ('Rosalind_2391', 'Rosalind_2323')]

data = {'Rosalind_0442': 'AAATCCC',
        'Rosalind_0498': 'AAATAAA',
        'Rosalind_2323': 'TTTTCCC',
        'Rosalind_2391': 'AAATTTT',
        'Rosalind_5013': 'GGGTGGG'}

def overlap_graph(data, n):
    edges = []
    for ke1, val1 in data.items():
        for ke2, val2 in data.items():
            if ke1 != ke2 and val1[-n:] == val2[:n]:
                edges.append(ke1 + '    ' + ke2)
    return edges

print(overlap_graph(data,3))

['Rosalind_0498    Rosalind_0442', 'Rosalind_0498    Rosalind_2391', 'Rosalind_2391    Rosalind_2323']

13. Calculating Expected Offspring(计算子代期望)

image.png

解题思路
- 以上六组生成子代为显现的期望，假设每个亲本恰好产生两个子代

# coding='utf-8'
# method1
def fun(a, b, c, d, e, f):
    x1 = 1 * a
    x2 = 1 * b
    x3 = 1 * c
    x4 = 0.75 * d
    x5 = 0.5 * e
    x6 = 0 * f

    return sum([x1, x2, x3, x4, x5, x6]) * 2

print(fun(1, 0, 0, 1, 0, 1))

3.5

# method2

input = '1 0 0 1 0 1'
nums = [int(i) for i in input.split(' ')]
es = [0.75 * nums[3], 0.5 * nums[4]]
for i in range(3):
    es.append(nums[i])
print(sum(es) * 2)

3.5

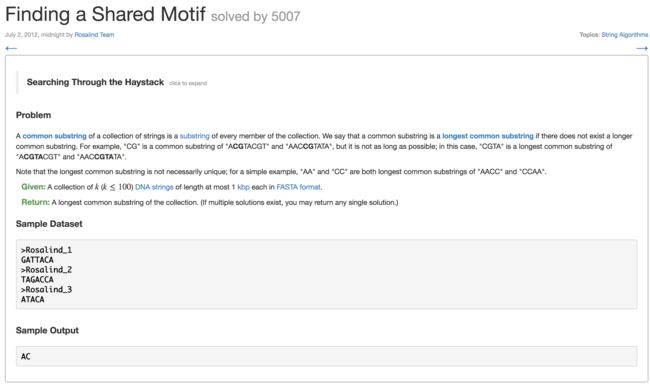
14. Finding a Shared Motif(找共有的模体)

image.png

解题思路
- 把序列都拆了，做成一个list
- 遍历这个list 和原来三个序列比对
- 比对次数等于三次的为 shared Motif


def readfasta(filename, sample):
    fa = open(filename, 'r')
    fo = open(sample, 'w')
    res = {}
    rres = []
    ID = ''
    for line in fa:
        # 如果是">"开头的，就创建一个key键
        if line.startswith('>'):
            ID = line.strip('\n')
            res[ID] = ''
        # 如果不是">"开头的，在这个key键下添加value值
        else:
            res[ID] += line.strip('\n')
    # 把value值提取出，写入sample文件
    for value in res.values():
        rres.append(value)
        fo.write(value + '\n')
    #返回 ['TAGACCA','ATACA','GATTACA']
    return rres


def fragement(seq_list):
    res = []
    seq = seq_list[0]
    for i in range(len(seq)):
        s_seq = seq[i:]
        for j in range(len(s_seq)):
            res.append(s_seq[:(len(s_seq) - j)])
    # 返回res列表的所有组合
    return res


def main(infile, sample):
    seq_list = readfasta(infile, sample)
    frags = fragement(seq_list)
    frags.sort(key=len, reverse=True)  # 从长到短排列
    for i in range(len(frags)):
        ans = []
        for j in seq_list:
            # 把"所有组合"匹配到"列表"里面，有些匹配1次，有些匹配2次，
            # 匹配三次的就是share_motif
            r = j.count(frags[i])
            if r != 0:
                ans.append(r)
        # 判断匹配是否大于等于三次
        if len(ans) >= len(seq_list):
            # 打印匹配大于等于三次的
            print(frags[i])
            break

main('14_Finding_a_shared_motif.txt', 'sample.txt')

TA

def LongestSubstring(string_list):
    longest = ''
    # 从0读到序列长度
    for start_index in range(len(string_list[0])):
        # 倒着读序列长度
        for end_index in range(len(string_list[0]), start_index, -1):
           # 两指针相遇，跳出循环
            if end_index - start_index <= len(longest):
                break
            # string_list[0][start_index:end_index] 任意组合string_list
            # 判断如果为true,执行下一条
            elif CheckSubstring(string_list[0][start_index:end_index], string_list):
                # 返回匹配到的片段
                longest = string_list[0][start_index:end_index]

    return longest


def CheckSubstring(find_string, string_list):
    for string in string_list:
        # 片段大于序列长度不用比了，片段不在序列里面也不用比了。
        if (len(string) < len(find_string)) or (find_string not in string):
            return False
    return True

# 把文件读成字典
# {'>Rosalind_1': 'GATTACA', '>Rosalind_2': 'TAGACCA', '>Rosalind_3': 'ATACA'}
seq = {}
seq_name = ''
with open('14_Finding_a_shared_motif.txt') as f:
    for line in f:
        if line[0] == '>':
            seq_name = line.rstrip()
            seq[seq_name] = ''
            continue
        else:
            seq[seq_name] += (line.rstrip()).upper()


if __name__ == '__main__':
    # ['GATTACA', 'TAGACCA', 'ATACA']
    dna = []
    for seq_name in seq:
        dna.append(seq[seq_name])

    lcsm = LongestSubstring(dna)
    print(lcsm)
    with open('014_LCSM.txt', 'w') as output_data:
        output_data.write(lcsm)

TA

image.png

15. Independent Alleles（独立的等位基因，即孟德尔第二定律）

image.png

解题思路
- 从第0代1个AaBb的个体开始，所有个体都与AaBb的个体交配产下2个后代，遵循孟德尔第二定律。
- 要求在第k代中至少有N个AaBb个体的概率。

import itertools

def f(k, n):
    p = []
    # 孩子数量
    child_num = 2 ** k
    for i in range(n):
        # 把小于n的概率算出来
        # combinations('ABCD', 2)       AB AC AD BC BD CD
        # AaBb亲代生成AaBb子代的概率为0.25
        p.append(len(list(itertools.combinations([x for x in range(child_num)], i))) * (0.25 ** i) * (0.75 ** (child_num - i)))

    return 1 - sum(p)
print(f(2, 1))

0.68359375

from scipy.misc import comb
k, N = 2,1

prob = 0
for i in range(N, 2**k + 1):
    # 把大于N 的概率一个一个加起来
    prob += comb(2**k, i) * ((1/4.0)**i) * ((3/4.0)**((2**k)-i))

print (prob)

0.68359375

欢迎交流

ROSALIND Bioinformatics(11-15)

11. Mortal Fibonacci Rabbits (斐波那奇兔子有毒)

12. Overlap Graphs(重叠图)

13. Calculating Expected Offspring(计算子代期望)

14. Finding a Shared Motif(找共有的模体)

15. Independent Alleles（独立的等位基因，即孟德尔第二定律）

你可能感兴趣的:(ROSALIND Bioinformatics(11-15))