Matlab时间序列分析

时间序列分析需要解决的问题

假设我们有这么一段数据（采样自移动公司某段时间的开户客户数目）
下载地址，包含本实验用到的数据/资料以及全部代码，实验报告，引用请告知，关注并留言获取提取码，或者到我的csdn下载进行下载

我们可以发现，在数据中似乎有种明显的趋势规律，或许还存在一定的周期性。但是，我们却不好描述这种趋势或者说是周期，因为数据中存在一定的随机因素模糊了我们的判断。在进行时间序列数据分析时，我们大部分的目的都是想从中找出可以表达的规律以便于我们对未来做预测。
在这里，我们把时间序列数据分解为以下三项：

真实数据=趋势项+周期项+随机项
趋势性：例如随时间变化的一次函数/多次函数/幂函数趋势等
周期项：周期规律
随机项：在这里可以理解为噪声，但是这些噪声也是存在规律的。

不难发现，趋势性和周期项都不难描述，难以刻画的是随机项变化。而如果我们真正能预测随机项的变化，那么我们就基本上可以预测整个数据下一步的走势了。

时间序列分析的步骤

• 观测数据（均值，周期等）
• 数据预处理
• 平稳化–去趋势与去周期，剩余随机项
• 用类似于回归/滑动平均的思想来 拟合随机项
  1.判断去趋势去周期后的数据是否平稳
  2.计算数据的自相关函数和偏相关函数
  3.根据自相关/偏相关函数性质决定选用什么模型来拟合随机项

4.模型定阶和拟合参数的求解
5.模型检验

• 模型最终实现功能：将周期项/趋势性/随机项结合，是一个关于时间变化的函数，这个函数可以在一定程度上对未来数据进行预测。

如何实现每个步骤

去趋势/去周期

运用差分算子可以去趋势和周期，其中N阶差分用于具有N阶多项式趋势的数据去趋势，N步差分用于具有N步周期的数据去周期。

偏相关/自相关函数的计算

可以运用matlab自带函数，也可以自己编写。

模型定阶

可以参考AIC/BIC等定阶方法

模型检验

通过计算LB统计量和卡方统计量，判断拟合的误差项是否为白噪声序列，如果是，则检验通过。

一个具体的案例 --移动开户数分析

我们有一份移动公司两年间共计700余天的每日开户树，我们想探寻其中的随机因素。

数据观察

变化趋势

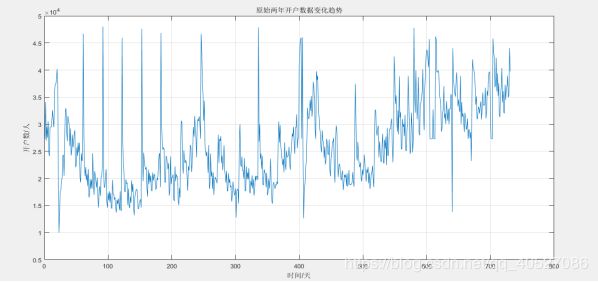
   图一.原开户数据趋势变化的观察

可以发现，开户数在局部区间的极值变化具有一定的周期性。但是数据太多且有点杂乱。
为了更好的观察数据的规律，拟将数据进行滑动平均处理，在一定程度上更能看出规律性。并且，依据两年的月数天数变化，设置标记每月天数变化的向量，计算每月，每个季度，每年的平均开户数进行观察。计算并绘制得到下图：

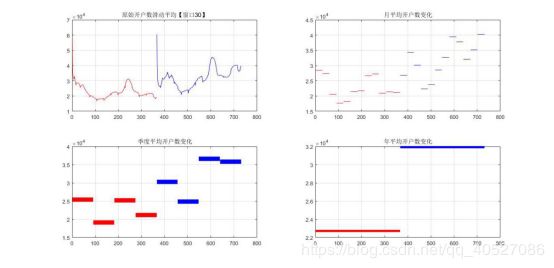
图二.开户数据趋势变化周期的观察

上图红色标记为2012年，蓝色标记为2013年。总的看来均有上升的趋势。图二左上角绘制的是2012和2013的开户数滑动平均观察（使用matlab smooth函数，滑动窗口设置为30），容易发现在年这个层面上趋势具有较大的相关性，一年显然可以是一个大周期的刻画。但是这个周期太大了，如果选取这个周期做去季节性，显然会损失大量数据。因此，我们想找到一个更小的周期来刻画，其实我们还可以发现图一中有明显的小起伏，经验证起伏平均间隔为30即一个月，那么一个月是否为一个周期呢？右上图是按月进行平均的统计值绘制，起伏貌似没有什么规律。但是还是可以作为参考。左下角图绘制的是季度的平均开户数变化，可以发现两个季度为一个周期，因为起伏在两个周期中进行。右下角图绘制的是年平均变化图，如我们所料，随着移动互联网的普及，2013年开户平均数比2012年高。

综上观察，我们可以得出以下结论：
1.一个月应该是一个最小周期，两个季度是一个中周期，一年为一个确定的大周期。
2.开户人数有明显的上升趋势。
3.由观测值我们可以认为存在异常值。

数据预处理

2.1缺失值处理
数据中不存在缺失值
2.2异常值处理
拟采用三倍标准差即拉以达法则筛选异常值，考虑到时间序列的短期影响性，用其周围值平均代替。

去趋势与去周期

进行了简单的观察和数据预处理后，我们开始正式进行时间序列平稳化的操作。考虑到有两年，我们从单独考虑2012，2013，然后集中考虑2012和2013来进行处理和检验。
3.1去趋势
由于数据变化有一定的集中性，且有滑动平均看来近似可以用一次函数拟合。所以采用一次差分的方法去除数据的趋势项。这里采用diff函数实现一次差分。去趋势后，我们进行了如下的观察：

图三.周期为一个月的检验图

我们发现相邻极值点间的时间差距十分接近于一个月，这让我们欣喜万分。

3.2去周期
由以上的观察数据和去趋势后数据综合考虑，采用一个月作为周期是个不错的选择。这里自定义d步差分函数对去趋势后的数据进行去周期的处理。
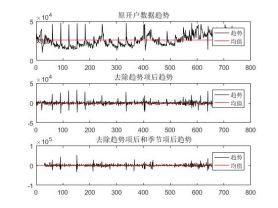
经过3.1和3.2,我们得到如下结果：

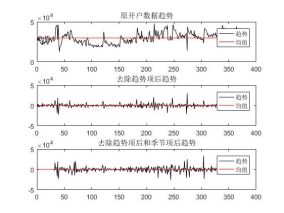
图四.2012年去趋势和去周期比较图 图五.2013年去趋势和去周期比较图

图六.2012-2013年去趋势和去周期比较图

肉眼看来，效果还算不错，从均值线看来均值均十分接近于0。为了更客观的看待平稳的效果，采用自相关图还进行平稳性的验证。

自相关性平稳性检验结果如下：

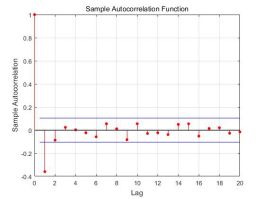
图七.自相关图检验平稳性

从自相关图看来，经过去趋势和去周期后的数据的确是平稳的。 经过以上步骤，我们就成功的将非平稳的时间序列转换为了平稳的时间序列，得到了随机误差项的表示。

截至目前以上代码总结：

%% 计算月平均，季度平均，年平均意图找寻周期规律
% 输入开户数据
% 输出各有用的统计量
function [months_mean,seasons_mean,years_mean,month_starts,month_ends,season_starts,season_ends] = Calu_mean(open_nums)
t = 1:length(open_nums);
nums = open_nums;
month_days = [0,31,29,31,30,31,30,31,31,30,31,30,31,31,28,31,30,31,30,31,31,30,31,30,31]; 
season_days = [0,sum(month_days(2:4)),sum(month_days(5:7)),sum(month_days(8:10)),sum(month_days(11:13))...
    ,sum(month_days(14:16)),sum(month_days(17:19)),sum(month_days(20:22)),sum(month_days(23:25))];
% calu the month_mean nums
months_mean = zeros(1,24);
month_starts = zeros(1,24);
month_ends = zeros(1,24);
for ii = 1:length(month_days)-1
    start_day = sum(month_days(1:ii))+1;
    end_day = sum(month_days(1:ii+1));
    month_starts(ii) = start_day;
    month_ends(ii) = end_day;
    months_mean(ii) = mean(nums(start_day:end_day));
end

%% 去趋势和周期函数
% 输入预处理后的时序数据向量vector和观察数据变化人为认定的周期T
% 输出去趋势后的向量数据detrend_data和去趋势去周期后的向量数据detrend_deT_data
function [detrend_data,detrend_deT_data] = Detrend_plot(vector,T)
    subplot(3,1,1)
    plot(1:length(vector),vector,'k')
    hold on
    plot(0:length(vector),mean(vector)*ones(1,length(0:length(vector))),'r')
    text(1,mean(vector),'均值')
    legend('趋势','均值')
    title('原开户数据趋势')
    % 去趋势项
    detrend_data = diff(vector,1);
    subplot(3,1,2)
    plot(1:length(detrend_data),detrend_data,'k')
    hold on
    plot(0:length(detrend_data),mean(detrend_data)*ones(1,length(0:length(detrend_data))),'r')
    legend('趋势','均值')
    title('去除趋势项后趋势')
    % 去季节项
    detrend_deT_data = zeros(length(detrend_data),1);
    for i=1:length(detrend_data)
        if(i<=T)
            detrend_deT_data(i) = [];
        else
            detrend_deT_data(i) = detrend_data(i)-detrend_data(i-T);
        end
    end
    subplot(3,1,3)
    plot(1:length(detrend_deT_data),detrend_deT_data,'k')
    hold on
    plot(0:length(detrend_deT_data),mean(detrend_deT_data)*ones(1,length(0:length(detrend_deT_data))),'r')
    legend('趋势','均值')
    title('去除趋势项后和季节项后趋势')
end

%% 主函数脚本，运行该脚本将输出以上所有结果
clearvars
%% 读取数据并预处理
open_nums = xlsread('移动通知户开户数.xlsx',1,'B2:B732');
%% 计算月平均，季度平均，年平均并绘图找周期规律,并处理异常值
figure(1),[months_mean,seasons_mean,years_mean,month_starts,month_ends,season_starts,season_ends] = Calu_mean(open_nums);
[m,n] = find(abs(open_nums-mean(open_nums))>2*std(open_nums));
open_nums(m) = mean(open_nums);
%% 尝试进行去趋势和去周期,考虑到存在多重周期，将年份分开按照月为周期去除周期（其中每月为多少天根据两年分别不同）
data_2012 = open_nums(1:366);
data_2013 = open_nums(367:end);
figure(2),[detrend_data2012,detrend_deT_data2012] = Detrend_plot(data_2012,30);% 2012开户数变化趋势
figure(3),[detrend_data2013,detrend_deT_data2013] = Detrend_plot(data_2013,31);% 2013开户数变化趋势
figure(4),[detrend_data,detrend_deT_data] = Detrend_plot(open_nums,30);% 2012-2013开户数变化趋势
figure(5),subplot(411),autocorr(open_nums),title('原数据自相关图')% 自相关图分析
subplot(412),autocorr(detrend_data),title('2012年随机项自相关图')
subplot(413),autocorr(detrend_deT_data2013),title('2013年随机项自相关图')
subplot(414),autocorr(detrend_deT_data2013),title('2012-2013年随机项自相关图')
clearvars month_starts month_ends season_starts season_ends data_2012 data2013

截至目前，我们编写的代码所完成的工作有：
1.观察数据
2.数据预处理
3.去趋势，去周期
4.计算了偏相关函数和自相关函数

我们还需要进行的工作是：
1.判断处理后的随机项是否平稳，判断自相关/偏相关函数的拖尾性/截尾性，以确定采用什么模型来拟合随机项。去均值使该时间序列变为零均值平稳过程。

2.确定模型后，确定采用几阶进行拟合，并求解参数
3.模型检验

******* 休息好了吧，我们继续

判断去趋势和去周期后数据的平稳性

 图一  处理后的数据               图二  处理后数据的20期自相关系数

自相关系数定义为：

由图二观察知道，当|h|>1时，自相关系数为近似为0.认为自协方差函数(自相关函数)有“截尾性”.可以使用MA(1)模型。为了考虑能否使用ARMA模型，进一步进行讨论。

转换为零均值平稳序列

采用mean函数计算该序列的均值，处理如下：
随机变量总体X 的样本的均值估计量：

转换前后序列变化如下：

  图三 非零均值平稳序列                图四 零均值平稳序列 

3.无偏/有偏自相关函数的估计
自协方差函数（或自相关函数）的样本估计量通常有两种类型：
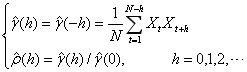（3.3.1）
（3.3.2）
关于两种估计量,前人曾经做过比较，G.M.Jenkins 结论：
1.估计量（ 3.3.1） 更满意。
2.其中（3.3.1）是自相关函数的有偏估计，（3.3.2）是自相关函数的无偏估计。
3.（3.3.1）式定义的估计量收敛于零的速度更快。
4.由(3.3.1)式定义的样本自协方差函数矩阵（或相关矩阵）是正定的

根据两种自相关系数的计算公式，我们可以自己编写函数计算自相关函数如下
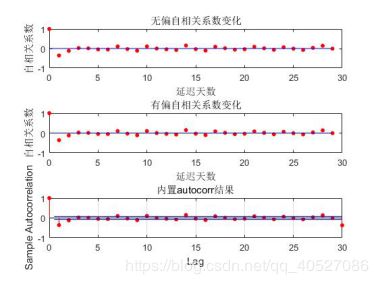
其中函数输入为零均值的平稳序列，输出为一组无偏估计的自相关系数，一组为有偏的自相关系数。完成自己的函数编写后，选择计算前面30期自相关系数与matlab自带autocorr进行比较。
自定义计算无偏和有偏两种自相关系数代码：

function [unbiased_autocorr,biased_autocorr] = my_autocorr(time_vector)
%% 函数定义,计算无偏和有偏两种自相关系数
n = length(time_vector);
unbiased_autocorr = zeros(n,1);
biased_autocorr = zeros(n,1);
% 延迟期数从0到n
for h = 0:n
    omega = 0;
    % 累加从t=1到n-h
    for t = 1:n-h
        omega = omega+time_vector(t)*time_vector(t+h);
    end
    unbiased_autocorr(h+1) = omega/(n-h);
    biased_autocorr(h+1) = omega/n;
end
% 自相关函数转换为自相关系数
unbiased_autocorr = unbiased_autocorr/unbiased_autocorr(1);
biased_autocorr = biased_autocorr/biased_autocorr(1);
%% 绘图比较
n_compare = 30;
figure()
subplot(311) 
plot(0:n_compare-1,unbiased_autocorr(1:n_compare),'ro','MarkerFaceColor','r','markersize',4)
hold on,plot(0:n_compare-1,zeros(1,n_compare),'b')
title('无偏自相关系数变化'),xlabel('延迟天数'),ylabel('自相关系数')
subplot(312) 
plot(0:n_compare-1,biased_autocorr(1:n_compare),'ro','MarkerFaceColor','r','markersize',4)
hold on,plot(0:n_compare-1,zeros(1,n_compare),'b')
title('有偏自相关系数变化'),xlabel('延迟天数'),ylabel('自相关系数')
subplot(313) 
autocorr(time_vector,n_compare),title('内置autocorr结果')

结果如图：

     图五  前30期自相关系数比较图

由图，计算结果与内置函数结果十分接近，验证了自己构建的函数的准确性。

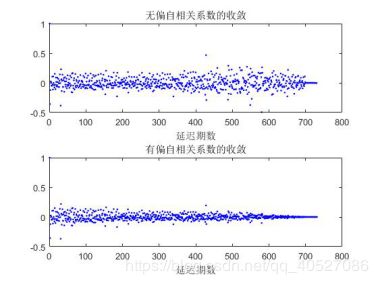
图六 无偏/有偏自相关系数的收敛速度比较

可以看出。该图验证了第三个结论，即有偏估计定义的估计量收敛于零的速度更快，且从收敛趋势看来效果更好。

4.偏相关系数的估计和比较
计算偏相关系数有两种方法，直接求解和递推求解。这里考虑递推求解。运用3求解得到的自相关系数一步步递推得到所有的偏相关系数。
4.1 直接求解
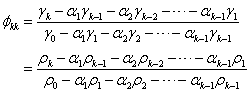（3.4.1）
由最优线性估计的计算公式，应用矩阵按行（列）展开式的性质可得
（3.4.2）
4.2 递推求解
（3.4.3）
递推过程：

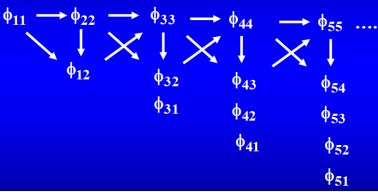
       图七 递推求解过程

理解以上递推思想后，利用3计算出来的自相关系数，编写函数如下:
其中输入为自相关系数和之前的零均值序列。前者用于递推，后者用于利用matlab自带函数parcorr对自定义的函数计算值进行检验。
代码：

function [customed_parcorr] = my_parcorr(time_vector,auto_corr)
%% 函数定义
n = length(auto_corr);
customed_parcorr = zeros(n,n);
customed_parcorr(1,1) = auto_corr(2);
for k = 1:n-2
    sum1 = 0;
    sum2 = 0;
    for j = 1:k
        sum1 = sum1 + auto_corr(k+2-j)*customed_parcorr(k,j);
        sum2 = sum2 + auto_corr(j+1)*customed_parcorr(k,j);
    end
    customed_parcorr(k+1,k+1) = (auto_corr(k+2)-sum1)/(1-sum2);
    for j = 1:k
        customed_parcorr(k+1,j) = customed_parcorr(k,j) - customed_parcorr(k+1,k+1)*customed_parcorr(k,k+1-j);
    end
end
%% 绘图比较
a = diag(customed_parcorr);
subplot(211)
compare_n = 40;
parcorr(time_vector,compare_n)
subplot(212)
plot(1:compare_n,a(1:compare_n),'ro','markerfacecolor','r','markersize',4)
hold on,plot(1:compare_n,zeros(1,compare_n),'b')
ylim([-0.5,1])
title('自定义偏相关计算值')
xlabel('延迟天数'),ylabel('偏相关系数')

结果如图八所示：

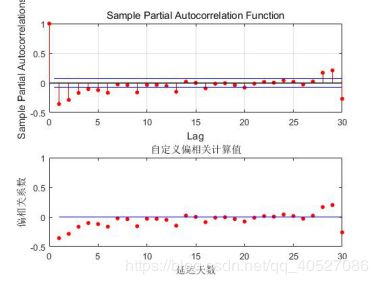
图八 自定义偏相关系数计算值与parcorr前30期计算值比较

由比较图看来，计算结果相当。
由图八可知，偏相关系数具有拖尾性。

截至目前，除了上面给过的代码外，新的部分计算代码给出如下：

%% 主函数运行脚本
clearvars
%% 读取数据并预处理
open_nums = xlsread('移动通知户开户数.xlsx',1,'B2:B732');
%% 计算月平均，季度平均，年平均并绘图找周期规律,并处理异常值
figure(1),[months_mean,seasons_mean,years_mean,month_starts,month_ends,season_starts,season_ends] = Calu_mean(open_nums);
[m,n] = find(abs(open_nums-mean(open_nums))>2*std(open_nums));
open_nums(m) = mean(open_nums);
%% 尝试进行去趋势和去周期,考虑到存在多重周期，将年份分开按照月为周期去除周期（其中每月为多少天根据两年分别不同）
data_2012 = open_nums(1:366);
data_2013 = open_nums(367:end);
figure(2),[detrend_data2012,detrend_deT_data2012] = Detrend_plot(data_2012,30);% 2012开户数变化趋势
figure(3),[detrend_data2013,detrend_deT_data2013] = Detrend_plot(data_2013,31);% 2013开户数变化趋势
figure(4),[detrend_data,detrend_deT_data] = Detrend_plot(open_nums,30);% 2012-2013开户数变化趋势
figure(5),subplot(411),autocorr(open_nums),title('原数据自相关图')% 自相关图分析
subplot(412),autocorr(detrend_data),title('2012年随机项自相关图')
subplot(413),autocorr(detrend_deT_data2013),title('2013年随机项自相关图')
subplot(414),autocorr(detrend_deT_data),title('2012-2013年随机项自相关图')
clearvars month_starts month_ends season_starts season_ends data_2012 data2013
%% 平稳序列去均值变为零均值平稳序列
zeromean_detrend_deT_data = detrend_deT_data-mean(detrend_deT_data);
[unbiased_autocorr,biased_autocorr] = my_autocorr(zeromean_detrend_deT_data);
%% 计算偏相关函数
[customed_parcorr] = my_parcorr(zeromean_detrend_deT_data,biased_autocorr);

************** 休息一会，我们继续

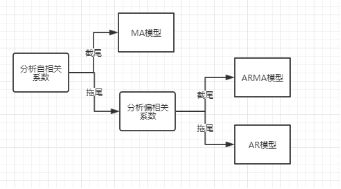
处理后数据适用的模型判别

观察平稳序列的自相关函数和偏相关函数，通过是否拖尾/结尾判断使用的模型。

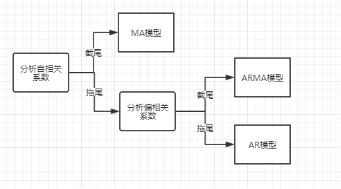
图*1 模型判别流程图

通过上面的分析，自相关系数和自偏相关系数均呈现拖尾性，故使用ARMA模型进行进一步分析。

3.ARMA模型的参数估计和定阶
拟函数法进行求解，求解步骤如下：

3.1初定阶数p和q,运用Yule-Walker求解逆函数I
3.2求解MA滑动平均系数
3.3求解AR自回归系数
3.4在求出所有参数后，利用极大似然法残差平方和求方差，算出AIC/BIC指标
3.5重复不走3.1-3.4，在一定大范围内找出极小BIC值对应的阶数p，q

4.参数检验和定阶的进一步修正
通过模型的显著性检验和参数的显著性检验，在参数估计和定阶最小BIC情况下对应的结束p,q附近进行，最终找到最佳的ARMA阶数为ARMA（1，1），参数求解为

经检验残差序列为白噪声，认为模型效果可以接受。
1.适用模型识别
首先，我们需要做的是根据动态数据，从各类模型族中选择与实际过程相吻合的模型；
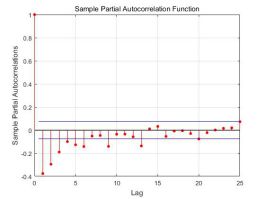
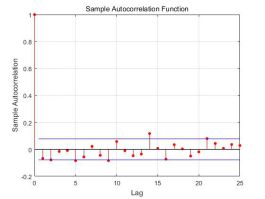
即处理后的平稳序列应该用什么模型来表示最为合理。经过前期的预处理，去趋势和去周期，得到平稳时间序列的自相关系数，偏相关系数如下图1.1。

                图1.1 平稳序列的自相关/自协相关系数

不难发现，该平稳序列的自相关系数和自偏相关系数均有拖尾的性质，且自相关拖尾阶数较高分布在32-35阶左右，而自偏相关系数拖尾阶数较低，分布在12-20之间。综上，拟采用ARMA模型对其进行拟合。
2.ARMA模型的参数估计和定阶
确定好适用的模型之后，下一步我们要进行的是对确定的模型类别，定出模型中的阶数p 和 q ，这里采用先大范围搜索，在搜索的结束中求的模型的参数估计——自回归系数和滑动平均系数，并由此求出拟合残差的方差。最后，计算每个阶数下对应的AIC/BIC进行比较，这里适用最小BIC值对应的阶数和参数估计做下一步的分析。

2.1 方法的选取
课件4.3关于ARMA模型的参数估计中介绍了两种估计参数的方法，对这两种方法的理解如下：
*ARMA模型参数的矩估计：通过Y-W方程求解出自回归系数，利用MA(q)模型参数的线性迭代法或牛顿—拉裴森算法求得滑动平均系数，最后合并可得拟合模型。这种方法 矩估计方法精度较低，通常只能作为其他迭代参数估计算法的初值。
*模型参数的初估计法—逆函数法：利用可逆域的逆转形式进行求解。这种方法仅涉及到线性方程的求解，计算简单便于实现。
综合上述两种方法，考虑到逆函数法对于低阶或高阶模型都很有效且求解方便。这里采用逆函数法对模型参数进行估计，逆函数法求解步骤如下
逆函数法求解步骤

1.令P(*) = max(p,q)+q,用y—w方法估计AR(p*)的 p* 个自回归参数，作为
相应的ARMA( p, q)模型的前 p*个逆函数值.
2.求解线性方程组得到滑动平均系数的估计。
3.将前两步的结果代入课件4.3.6公式，求得自回归系数的估计。

模型参数和求解和定阶

2.2.1模型的定阶指标
*最终预报误差准则（PDE)

其中，方差依赖于k, 其大小反映了模型与数据的拟合程度。第一个因子随 k 增大而增大, 放大了残差方差的不确定性影响.
*最小信息准则(AIC)

AIC准则可应用于ARMA模型及其他统计模型(如多项式回归定阶).能在模型参数极大似然估计的基础上，对于ARMA(p, q)的阶数和相应的参数，同时给出一种最佳估计.
*BIC准则

AIC准则避免了统计检验中由于选取置信度而产生的人为性，为模型定阶带来许多方便. 但AIC方法未给出相容估计.
**注意：AIC阶数估计一般偏高，BIC阶数估计偏低。这里适用BIC准则进行初始阶数的定阶，取BIC值最小下对应的阶数p,q即为初始定阶。
2.2.2 模型的求解
观察之前的自相关系数图和自偏相关系数图，初定ARMA模型初始阶数的选取p和q均在1-20阶内，利用逆函数求解并算的每个p,q下参数对应的BIC值，取最小BIC对应的p,q即为初定的阶数。不同怕p,q下对应的BIC值如下图。

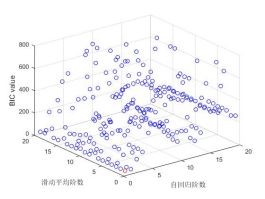
图2.2.2 BIC值的变化

由BIC值的变化我们可以看出，在取ARMA(1,1)时BIC值最小。此时ARMA(1,1)模型建立如下：

定阶的进一步修正-模型的检验

确定好最小BIC准则下的参数估计值和模型阶数p和q后，我们知道——以上各个问题是相互关联的，需整体进行系统化的模型优化. 而根据已有的一组样本数据建立模型，对模型阶数和参数作出判断和估计，是重要的两部分工作.所以最后，我们需要在已经初定的阶数周围小范围内进行搜索和检验，通过模型的有效性检验的参数的显著性检验进一步优化模型，寻找最优的阶数和参数估计值。统计模型只是对生成观测数据真实过程的近似，在模型拟合后，还需要进行模型的有效性检验，及检验拟合模型对序列中信息的提取是否充分。模型的有效性检验即对残差的白噪声检验。
观察残差序列及其自相关系数如下图所示：

图3.1 残差序列自相关系数

可以发现序列间没有相关性，不具有拖尾和截尾的性质，可以初步判断改模型是可靠的。为了进一步验证残差序列是否为白噪声序列，下面进行LB统计量的检验结果如下：
延迟期数 LB统计量 卡方统计量

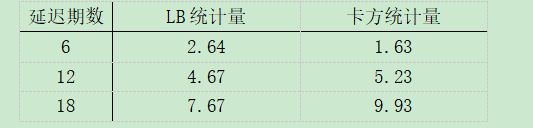
由LB统计量小于对应的卡方统计量，认为该序列可以认为是白噪声序列。模型效果较好，模型检验通过。
到此，我们所有工作已经完毕。如果有什么疑问，欢迎留言，我会一一解答。

新部分的代码：
1主函数 main1.m
实现功能：读取处理后的平稳数据进行建模，通过观察自相关/自偏相关系数确定选用ARMA模型，在一定确定的阶数范围内求模型的参数估计，根据最小BIC准则初定p,q的选择，最后通过模型的有效性检验和参数的显著性检验确定最终的参数估计和阶数。

% 读取处理后的平稳时间序列

    processed_data = csvread('detrend_deT_data.csv');
    figure(1)
    autocorr(processed_data,60)
    figure(2)
    parcorr(processed_data,25)
    data_autocorr = autocorr(processed_data,600);
    % 自相关系数向量转换为自相关系数矩阵
    autocorr_matrix = vec2mat(data_autocorr);
    max_p = 15;
    max_q = 20;
    AICs = ones(max_p,max_q);
    BICs = ones(max_p,max_q);
    N = 600;
    for p=1:20
        for q = 1:20
            % 计算I
            P = max(p+q)+q;
            I = autocorr_matrix(1:P,1:P)\autocorr_matrix(1,2:P+1)';
            % 计算MA部分的滑动平均系数
            seta = calu_MA_parameter(I,p,q);
            % 计算AR部分的自回归系数
            fine = calu_AR_parameter(seta,I,p,q);
            % 计算方差
            residual_var = calu_var(p,q,fine,seta,N,processed_data);
            % 计算AIC和BIC并存储
            [AICs(p,q),BICs(p,q)] = calu_AIC_BIC(p,q,N,residual_var);
        end
    end

% 找出最小BIC下的阶数p,q
[min_BIC_p,min_BIC_q] = find(BICs == min(BICs));
2.MA滑动平均系数的求解函数
[seta]=calu_MA_parameter（I,p,q）
函数输入：逆函数{ Ij }的估计I,给定的自回归和滑动平均阶数p和q
函数输出：滑动平均系数的估计值seta

function [seta]= calu_MA_parameter(I,p,q)
P = max(p,q);
I_matrix = zeros(q,q);
for ii = 1:q
    I_matrix(ii,:) = I(P+ii-1:-1:P+ii-q);
end
seta = I_matrix\I(P+1:P+q);
end

3.AR自回归系数的求解函数
[fine] = calu_AR_parameter(seta,I,p,q)
函数输入：逆函数{ Ij }的估计I,给定的自回归和滑动平均阶数p和q以及滑动平均系数seta
函数输出：自回归系数的估计值fine

function [fine] = calu_AR_parameter(seta,I,p,q)
fine = ones(1,p);
for ii = 1:p
    if ii>q
        seta(ii) = 0;
    end
    fine(ii) = seta(ii)+I(ii);
    for jj = 1:ii-1
        if (ii-jj)>0
            fine(ii) = fine(ii)-seta(jj)*I(ii-jj);
        end
    end
end

4.残差方差的计算函数
[residual_var]= calu_var(p,q,fine,seta,N,processed_data)
函数输入：逆函数{ Ij }的估计I,给定的自回归和滑动平均阶数p和q以及滑动平均系数seta，自回归系数fine，处理后的平稳序列。
函数输出：残差的方差

function [residual_var] = calu_var(p,q,fine,seta,N,processed_data)
error = zeros(1,N);
for ii = max(p,q)+1:N
    error(ii) = [1,-fine]*processed_data(ii:-1:ii-p)+seta'*error(ii-1:-1:ii-q)';
end
residual_var = (error*error')/N;
end

5.AIC/BIC指标的计算函数
[AIC,BIC] = calu_AIC_BIC(p,q,N,residual_var)
函数输入：给定的自回归和滑动平均阶数p和q，样本个数N以及残差方差。
函数输出：不同阶数下对应的AIC/BIC指标。

function [AIC,BIC] = calu_AIC_BIC(p,q,N,residual_var)
AIC = log(residual_var)+2*(p+q+1)/N;
BIC = log(residual_var)+log(N)*(p+q+1)/N;
End

6.计算LB统计量函数

lb = calu_LB(data, m)
函数输入：残差序列，延迟期数
函数输出：LB卡方统计量
function lb = calu_LB(data, m)
N = 25;
power_autocorr = 0;
data_autocorr = autocorr(data,25);
for k=1:m
    power_autocorr = power_autocorr+data_autocorr(k+1)^2/(N-k);
end
lb = N*(N+2)*power_autocorr;
End

7.自相关系数向量转为矩阵 vec2mat
[autocorr_matrix] = vec2mat(autocorr_vector)
函数输入：自相关系数函数输出：LB卡方统计量

function [autocorr_matrix] = vec2mat(autocorr_vector)
n = length(autocorr_vector);
autocorr_matrix = zeros(n);
for ii = 1:n
    autocorr_matrix(ii,ii:n) = autocorr_vector(1:n-ii+1);
end
autocorr_matrix = triu(autocorr_matrix)+tril(autocorr_matrix',-1);
end

yqol 编写不易，欢迎关注。