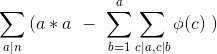HDU5528 迪利克雷卷积

被卡常了wuwuwu，这道题最后也没过，本机测试随机满数据不到2s，20000个1e9 4s

这种做法比较奇葩，我估计没人会这么做

这道题的本质是

左边那个希腊符号是欧拉函数，右边的是因子之和，都是积性函数，数论卷积后还是积性函数

所以n因式分解，化成答案变成几个积性函数的积

总复杂度 

啊，计蒜客上A了

详细的写下这道题的题解：容易的看出，答案是：            

等价于     

等价于     

等价于     

等价于     

等价于     

等价于     

设F是欧拉函数和因子和函数的数论卷积     

此题等价于     

F函数也是积性函数，因式分解后，按定义乘起来就行

#include
#include
#include
using namespace std;
typedef unsigned long long ll;
const ll N=4e4;
bool P[N+10];
vector V;
ll A[100],B[100];
ll F(ll x){
    ll ans=1;
    for(int i=0;V[i]*V[i]<=x;++i){
        if(x%V[i]==0){
            int a=0;
            while(x%V[i]==0){
                x/=V[i];
                ++a;
            }
            A[0]=1;
            for(int j=1;j<=a;++j){
            	A[j]=A[j-1]*V[i]*V[i];
			}
            for(int j=1;j<=a;++j){
            	A[j]+=A[j-1];
			}
			ans*=A[a];
    	}
    }
    if(x>1)ans=ans*(x*x+1);
    return ans;
}
ll G(ll x){
    ll ans=1;
    for(int i=0;V[i]*V[i]<=x;++i){
        if(x%V[i]==0){
            ll a=0;
            while(x%V[i]==0){
                x/=V[i];
                ++a;
            }
            ll b=0;
            A[0]=1;
            B[0]=1;
            for(int j=1;j<=a;++j)A[j]=A[j-1]*V[i];
            for(int j=1;j<=a;++j){
                B[j]=B[j-1]+A[j];
            }
            for(int j=1;j<=a;++j){
                b+=A[j-1]*(V[i]-1)*B[a-j];
            }
            b+=B[a];
            ans=ans*b;
        }
    }
    if(x>1)ans=ans*2*x;
    return ans;
}
int main(){
	//freopen("1.in","r",stdin);
	//freopen("1.out","w",stdout);
    for(int i=2;i<=N;++i){
        if(P[i]==0){
            V.push_back(i);
            for(int j=2*i;j<=N;j+=i)P[j]=1;
        }
    }
    ll T;
    scanf("%d",&T);
    while(T--){
        ll x;
        scanf("%lld",&x);
        if(x==0)printf("1\n");
        else printf("%lld\n",F(x)-G(x));
    }
}