图论模型（Dijkstra算法和Floyd算法）

图论模型

Dijkstra算法

概念

Dijkstra算法能求一个顶点到另一顶点最短路径。它是由Dijkstra于1959年提出的。实际它能给出从起始点到其他所有顶点的最短路径。（具体理论不在此赘述，如有需要请查阅相关文献）1

带权邻接矩阵

带权邻接矩阵是表示顶点之间相邻关系的矩阵。

矩阵中每个元素数值的确定遵从一下规则：

• xab x a b 表示从a地到b地的距离
• 如果a地与b地间双向通行，则 xab=xba x a b = x b a
• 如果a地到b地为单向通行，b地到a地无法直达，则 xba=inf x b a = i n f
• 如果a地与b地两地间无任何直达方法，则 xab=xba=inf x a b = x b a = i n f

代码

function [min, path] = dijkstra(w, start, terminal)
n = size(w, 1); label(start) = 0; f(start) = start;
for i = 1 : n
    if i ~= start
        label(i) = inf;
    end, end
s(1) = start; u = start;
while length(s) < n
    for i = 1 : n
        ins = 0;
        for j = 1 : length(s)
            if i == s(j)
                ins = 1;
            end,
        end
        if ins == 0
            v = i;
            if label(v) > (label(u) + w(u, v))
               label(v) = (label(u) + w(u, v));
            f(v) = u;
            end,
        end,
    end
v1 = 0;
    k = inf;
    for i = 1 : n
        ins = 0;
        for j = 1 : length(s)
            if i == s(j)
                ins = 1;
            end,
        end
        if ins == 0
            v = i;
            if k > label(v)
               k = label(v); v1 = v;
            end,
        end,
    end
    s(length(s) + 1) = v1;
    u = v1;
end
min = label(terminal); path(1) = terminal;
i = 1;
while path(i) ~= start
    path(i + 1) = f(path(i));
    i = i + 1;
end
path(i) = start;
L = length(path);
path = path(L : -1 : 1);
end

操作

在一个文件夹中放入上述代码构成的m文件，并在同一文件夹中新建脚本，构造带权邻接矩阵，并在脚本界面下运行脚本程序（注意不是运行函数程序）。

下面举个例子：

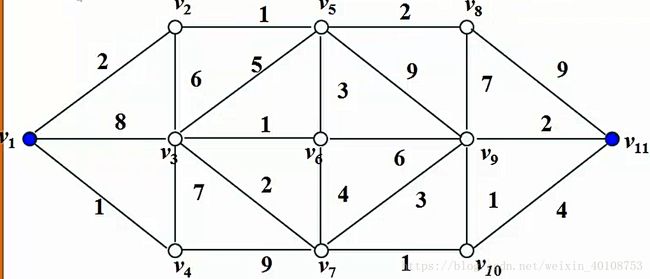
要计算从 v1 v 1 到 v11 v 11 的最短路径，可以构造含带权邻接矩阵的脚本如下：

weight = [  0   2   8   1 inf inf inf inf inf inf inf;
            2   0   6 inf   1 inf inf inf inf inf inf
            8   6   0   7   5   1   2 inf inf inf inf;
            1 inf   7   0 inf inf   9 inf inf inf inf;
          inf   1   5 inf   0   3 inf   2   9 inf inf;
          inf inf   1 inf   3   0   4 inf   6 inf inf;
          inf inf   2   9 inf   4   0 inf   3   1 inf;
          inf inf inf inf   2 inf inf   0   7 inf   9;
          inf inf inf inf   9   6   3   7   0   1   2;
          inf inf inf inf inf inf   1 inf   1   0   4;
          inf inf inf inf inf inf inf   9   2   4   0;];
[dis, path] = dijkstra(weight, 1, 11)   %1和11为始末点

运行后即可得到最短路径长为13，步骤为：1→2→5→6→3→7→10→9→11

Floyd算法

概念

Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话，首先我们的目标是寻找从点 i 到点 j 的最短路径。从动态规划的角度看问题，我们需要为这个目标重新做一个诠释（这个诠释正是动态规划最富创造力的精华所在）（同样的，具体理论不在此赘述，如有需要请查阅相关文献）2

代码

function [D, path, min1, path1] = floyd(a, start, terminal)
D = a; n = size(D, 1); path = zeros(n, n);
for i = 1 : n
    for j = 1 : n
        if D(i, j) ~= inf
            path(i, j) = j;
        end,
    end,
end
for k = 1 : n
    for i = 1 : n
        for j = 1 : n
            if D(i, k) + D(k, j) < D(i, j)
                D(i, j) = D(i, k) + D(k, j);
                path(i, j) = path(i, k);
            end,
        end,
    end,
end
if nargin == 3
    min1 = D(start, terminal);
    m(1) = start;
    i = 1;
    path1 = [ ];
    while path(m(1), terminal) ~= terminal
        k = i + 1;
        m(k) = path(m(i), terminal);
        i = i + 1;
    end
    m(i + 1) = terminal;
    path1 = m;
end

操作

与Dijkstra算法一样，需要构造带权邻接矩阵。脚本文件和上述代码构成的m文件也应在同一目录下。构造带权邻接矩阵遵循的规则同Dijkstra算法。

但与Dijkstra算法不同的是，脚本运行后的结果不同。运用Dijkstra算法进行计算能够直接得到最短路程长和具体步骤；而用Floyd算法计算后会得到两个矩阵。一个是 D 矩阵，一个是 path 矩阵，接下来详细说明一下：

同样是对于Dijkstra算法中的实例，我们通过Floyd算法来解。构造脚本如下：

weight = [  0   2   8   1 inf inf inf inf inf inf inf;
            2   0   6 inf   1 inf inf inf inf inf inf
            8   6   0   7   5   1   2 inf inf inf inf;
            1 inf   7   0 inf inf   9 inf inf inf inf;
          inf   1   5 inf   0   3 inf   2   9 inf inf;
          inf inf   1 inf   3   0   4 inf   6 inf inf;
          inf inf   2   9 inf   4   0 inf   3   1 inf;
          inf inf inf inf   2 inf inf   0   7 inf   9;
          inf inf inf inf   9   6   3   7   0   1   2;
          inf inf inf inf inf inf   1 inf   1   0   4;
          inf inf inf inf inf inf inf   9   2   4   0;];
[D, path] = floyd(weight)

运行后得到：

D =

 0     2     7     1     3     6     9     5    11    10    13
 2     0     5     3     1     4     7     3     9     8    11
 7     5     0     7     4     1     2     6     4     3     6
 1     3     7     0     4     7     9     6    11    10    13
 3     1     4     4     0     3     6     2     8     7    10
 6     4     1     7     3     0     3     5     5     4     7
 9     7     2     9     6     3     0     8     2     1     4
 5     3     6     6     2     5     8     0     7     8     9
11     9     4    11     8     5     2     7     0     1     2
10     8     3    10     7     4     1     8     1     0     3
13    11     6    13    10     7     4     9     2     3     0

path =

 1     2     2     4     2     2     2     2     2     2     2
 1     2     5     1     5     5     5     5     5     5     5
 6     6     3     4     6     6     7     6     7     7     7
 1     1     3     4     1     1     7     1     7     7     7
 2     2     6     2     5     6     6     8     6     6     6
 5     5     3     5     5     6     3     5     3     3     3
 3     3     3     4     3     3     7     3    10    10    10
 5     5     5     5     5     5     5     8     9     9    11
10    10    10    10    10    10    10     8     9    10    11
 7     7     7     7     7     7     7     9     9    10     9
 9     9     9     9     9     9     9     8     9     9    11

对于 D 矩阵，比如实例要求我们得到 1 到 11 的最短路径，那么我们读取 D 矩阵中的元素 a111=13 a 1 11 = 13 得到最短距离为13。

对于 path 矩阵，先读取元素 b111=2 b 1 11 = 2 ，这代表需要途径顶点 2 。接下来读取元素 b211=5 b 2 11 = 5 ，这代表接下来要途径顶点 5 ……最后读取元素 b911=11 b 9 11 = 11 ，结束操作，得到路径：1→2→5→6→3→7→10→9→11

以上两结果与通过Dijkstra算法得到的结果一致。这就体现双算法处理问题的优越性：如果两算法得到结果一致，则可以相互印证；如果结果不一致，则可以及时发现问题以查找原因。

---

1. DIjkstra算法是一种标号法：给赋权图的每一个顶点记一个数，称为顶点的标号（临时标号，称 T 标号，或者固定标号，称为 P 标号）。T 标号表示从起始顶点到该标点的最短路长的上界；P 标号则是从起始顶点到该顶点的最短路长。 ↩
2. Floyd算法思想原理：
   从任意节点 i 到任意节点 j 的最短路径无外乎两种可能：1、直接从 i 到 j ；2、从 i 经过若干个节点 k 到 j 。所以，我们假设 Dis（i， j）为节点 u 到节点 v 的最短路径的距离，对于每一个节点 k ，我们检查Dis（i， k） + Dis（k， j） < < Dis（i， j）是否成立，如果成立，证明从 i 到 k 再到 j 的路径比 i 直接到 j 的路径短，我们便设置DIs（i， j） = Dis（i， k） + Dis（k， j），这样一来，当我们遍历完所有节点 k ，Dis（i， j）中记录的便是 i 到 j 的最短路径的距离。 ↩