AC自动机入门详解

一.AC自动机的引入.

我们都知道KMP可以用来一个子串与母串之间的匹配，只需要通过一个next指针就可以实现$O(n+m)$匹配，已经达到了算法下界，是一个很优秀的算法了.

但是我们如何考虑多个子串与母串之间的匹配呢？

如果多个子串与母串之间的匹配用KMP来实现，效率可能就不那么高了，这可怎么办呢？这就是AC自动机的由来.

AC自动机是什么？其实就是在Trie树上跑KMP.


二.Trie树与KMP.

我们考虑单串时的KMP是怎么匹配的？利用的是next数组.

再考虑一下多串的一般套路？放进Trie树.

那么多串匹配怎么办？求Trie树上的next数组（在AC自动机里就叫fail指针了）！

考虑Trie树上在匹配一个串时，失配了怎么办？往fail指针跳！就像下面这张图：

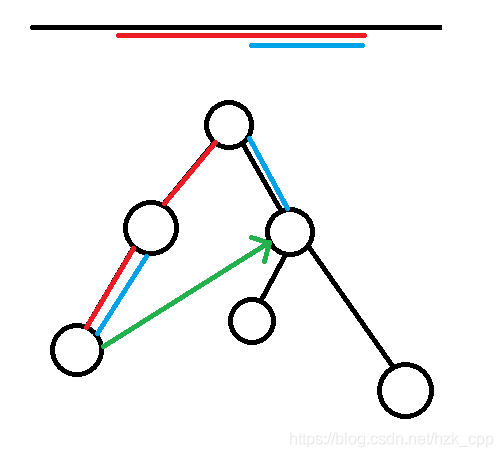
我们认为这张图中所有相同颜色的链与线段都是相同的，那么当Trie树上红色的链失配时我们想要继续匹配，就必须要让红色线段的一个后缀（例如蓝色线段）与Trie树上的另外一条以根为一段的链相同（例如蓝色的链）.fail指针也就是连接红色链的结尾与最长的满足条件的蓝色链的结尾（当然蓝色得比红色短）的一个指针（绿色箭头）.

是不是突然感觉AC自动机很容易啊…然而理解fail指针并不代表会构造fail指针（fail指针学过KMP与Trie树就能懂了吧）…


三.构造fail指针.

构造fail指针其实很简单，因为我们发现fail指针一定是从深度大的节点指向深度小的节点，又可以发现一个节点的fail指针可以通过它父亲的fail指针构造，所以我们选择使用BFS构造fail指针.

具体就是BFS每一层，一个节点的fail指针就用它父亲的fail指针尝试是否能匹配，不能匹配就继续跳fail指针，知道能匹配或跳到了根（与KMP的next很像的跳法）.

代码如下：

void Bfs_fail(){
  int co;
  tr[ord[co=1]=1].fail=1;
  for (int i=0;i<C;++i)
    if (tr[1].s[i]) tr[tr[1].s[i]].fail=1,q.push(tr[1].s[i]);
  while (!q.empty()){
  	int t=q.front();q.pop();
  	ord[++co]=t;
  	for (int i=0;i<C;++i)
	  if (tr[t].s[i]){
  	    int k=tr[t].fail;
  	    for (;k>1&&!tr[k].s[i];k=tr[k].fail);
  	    tr[tr[t].s[i]].fail=tr[k].s[i]?tr[k].s[i]:1;
  	    q.push(tr[t].s[i]);
  	  }
  }
}

值得注意的是，当我们去掉Trie树上fail指针外的边时，我们会发现Trie树上的节点与所有fail指针构成了一棵树！这棵树就被称为fail树.

既然我们有了一棵树，我们就可以对这棵树进行一些操作了.于是一些毒瘤题就这么应运而生（比如说BZOJ2434阿狸的打字机）.


四.Trie图.

Trie图是AC自动机的确定化形式，也就是说Trie图是一个DFA（自动机分DFA或NFA）.

Trie图的主要思想就是强行把一棵树变成图将$x$为空的儿子指针$s[i]$指向$x$的fail指针的$s[i]$，相当于直接把fail树上的边加到了Trie树上.这样做会使代码变得简洁一些，而且它能很大程度上帮你少跳一些指针（查询的时候就不用写while循环了，Trie图只需要跳一次指针就够了）.

代码如下：

void Bfs_fail(){
  int co;
  tr[ord[co=1]=1].fail=1;
  for (int i=0;i<C;++i)
    if (tr[1].s[i]) tr[tr[1].s[i]].fail=1,q.push(tr[1].s[i]);
    else tr[1].s[i]=1;
  while (!q.empty()){
  	int t=q.front();q.pop();
  	ord[++co]=t;
  	for (int i=0;i<C;++i)
	  if (tr[t].s[i]) tr[tr[t].s[i]].fail=tr[tr[t].fail].s[i],q.push(tr[t].s[i]);
	  else tr[t].s[i]=tr[tr[t].fail].s[i];
  }
}

五.运行.

接下来的运行以判定每一个串在母串中的出现次数为例.

查询最朴素的想法就是直接暴力在每一个点跳fail指针匹配，然而这样做是没有效率保证的.

考虑对于fail树，发现只要一个节点到根这一段可以匹配时，它在fail树上的父亲同样也会被匹配.所以我们只需要记录Trie树上每一个点被经过的次数，处理完之后让一个点的出现次数等于它的子树和.

普通AC自动机运行代码如下：

void Judge(char *s,int n){
  int k=1;
  for (int i=1;i<=n;++i){
  	for (;k>1&&!tr[k].s[s[i]-'a'];k=tr[k].fail);
  	if (tr[k].s[s[i]-'a']) k=tr[k].s[s[i]-'a'];
  	++cnt[k];
  }
  for (int i=cn;i>=1;--i){
  	int t=ord[i];
  	cnt[tr[t].fail]+=cnt[t];
  }
}

Trie图运行代码如下：

void Judge(char *s,int n){
  int k=1;
  for (int i=1;i<=n;++i) ++cnt[k=tr[k].s[s[i]-'a']];
  for (int i=cn;i>=1;--i){
  	int t=ord[i];
  	cnt[tr[t].fail]+=cnt[t];
  }
}

六.时间复杂度分析.

这里主要分析fail指针构造的时间复杂度.

我们考虑BFS时fail指针跳动的总次数，与KMP类似的，我们发现每跳一次fail指针都会使得深度减$1$，而深度最多增加串长次.所以对于Trie树中插入的每一个串构造fail指针时间复杂度都是与串长同级的，设总共往Trie中插入了$n$个字符，构造fail指针的总时间复杂度就是$O(n)$的.

同样的，在查询串的时候外层枚举i的时间复杂度为$O(m)$，也就是说深度最多增长了$m$次，所以fail指针的跳动次数最多也是$m$次，总时间复杂度就是$O(m)$.但是由于后面我们还需要遍历一遍Trie树，所以一次查询总时间复杂度为$O(n+m)$.


七.例题与代码.

例题：luogu5357.

普通AC自动机代码如下：

#include
  using namespace std;

#define Abigail inline void
typedef long long LL;

const int N=200000,M=2000000,C=26;

int n,id[N+9];
char s[M+9];
struct Trie{
  int s[C],fail;
}tr[N+9];
int cn;

void Build(){cn=1;}

int Insert(char *s,int n){
  int k=1;
  for (int i=1;i<=n;++i)
    if (tr[k].s[s[i]-'a']) k=tr[k].s[s[i]-'a'];
    else tr[k].s[s[i]-'a']=++cn,k=cn;
  return k;
}

int ord[N+9];
queue<int>q;

void Bfs_fail(){
  int co;
  tr[ord[co=1]=1].fail=1;
  for (int i=0;i<C;++i)
    if (tr[1].s[i]) tr[tr[1].s[i]].fail=1,q.push(tr[1].s[i]);
  while (!q.empty()){
  	int t=q.front();q.pop();
  	ord[++co]=t;
  	for (int i=0;i<C;++i)
	  if (tr[t].s[i]){
  	    int k=tr[t].fail;
  	    for (;k>1&&!tr[k].s[i];k=tr[k].fail);
  	    tr[tr[t].s[i]].fail=tr[k].s[i]?tr[k].s[i]:1;
  	    q.push(tr[t].s[i]);
  	  }
  }
}

int cnt[N+9];

void Judge(char *s,int n){
  int k=1;
  for (int i=1;i<=n;++i){
  	for (;k>1&&!tr[k].s[s[i]-'a'];k=tr[k].fail);
  	if (tr[k].s[s[i]-'a']) k=tr[k].s[s[i]-'a'];
  	++cnt[k];
  }
  for (int i=cn;i>=1;--i){
  	int t=ord[i];
  	cnt[tr[t].fail]+=cnt[t];
  }
}

Abigail into(){
  scanf("%d",&n);
  Build();
  for (int i=1;i<=n;++i){
  	scanf("%s",s+1);
  	id[i]=Insert(s,strlen(s+1));
  }
  scanf("%s",s+1);
}

Abigail work(){
  Bfs_fail();
  Judge(s,strlen(s+1));
}

Abigail outo(){
  for (int i=1;i<=n;++i)
    printf("%d\n",cnt[id[i]]);
}

int main(){
  into();
  work();
  outo();
  return 0;
}

Trie图：

#include
  using namespace std;

#define Abigail inline void
typedef long long LL;

const int N=200000,M=2000000,C=26;

int n,id[N+9];
char s[M+9];
struct Trie{
  int s[C],fail;
}tr[N+9];
int cn;

void Build(){cn=1;}

int Insert(char *s,int n){
  int k=1;
  for (int i=1;i<=n;++i)
    if (tr[k].s[s[i]-'a']) k=tr[k].s[s[i]-'a'];
    else tr[k].s[s[i]-'a']=++cn,k=cn;
  return k;
}

int ord[N+9];
queue<int>q;

void Bfs_fail(){
  int co;
  tr[ord[co=1]=1].fail=1;
  for (int i=0;i<C;++i)
    if (tr[1].s[i]) tr[tr[1].s[i]].fail=1,q.push(tr[1].s[i]);
    else tr[1].s[i]=1;
  while (!q.empty()){
  	int t=q.front();q.pop();
  	ord[++co]=t;
  	for (int i=0;i<C;++i)
	  if (tr[t].s[i]) tr[tr[t].s[i]].fail=tr[tr[t].fail].s[i],q.push(tr[t].s[i]);
	  else tr[t].s[i]=tr[tr[t].fail].s[i];
  }
}

int cnt[N+9];

void Judge(char *s,int n){
  int k=1;
  for (int i=1;i<=n;++i) ++cnt[k=tr[k].s[s[i]-'a']];
  for (int i=cn;i>=1;--i){
  	int t=ord[i];
  	cnt[tr[t].fail]+=cnt[t];
  }
}

Abigail into(){
  scanf("%d",&n);
  Build();
  for (int i=1;i<=n;++i){
  	scanf("%s",s+1);
  	id[i]=Insert(s,strlen(s+1));
  }
  scanf("%s",s+1);
}

Abigail work(){
  Bfs_fail();
  Judge(s,strlen(s+1));
}

Abigail outo(){
  for (int i=1;i<=n;++i)
    printf("%d\n",cnt[id[i]]);
}

int main(){
  into();
  work();
  outo();
  return 0;
}