赌徒输光 酒鬼回家 长期双方竞赛问题

前言：仅个人小记。

一、 问题原型

1. 赌徒手里有 x 元，每一局输的概率恒定为 p ，请问赌徒最终输光的概率？
2. 酒鬼徘徊（在坐标轴上左右移动）回家，目前酒鬼在坐标轴上 x 处，家在原点 0 处，请问酒鬼最终回到家的概率为多少？
3. 比特币中（中本聪的文章引入Gambler’s Ruin problem）两条链比赛输赢的概率问题，具体就是攻击者最终挖得的链比诚实者挖出的块儿要更多，此时攻击者就可以堂而皇之地取而代之，问题就是估算攻击者的胜算，以及当诚实者超前攻击者多少块的时候可以从概率上给予”无法篡改“这一保证。

二、抛出疑问

1. 赌徒输光指的是连续输掉手里的所有钱吗？是连续吗？
2. 输掉一元钱指的就是输掉本局吗？

三、前要分析和交代

1.赌徒刚开始手中的钱记为 $x_0$,到输光这个过程记为序列
$$x_0,x_1,...,x_n，x_i≠x_n,i<n,x_n=0$$即强调 “赌徒输光”指的是“赌徒第一次手里没钱，赌局结束”，不存在比如
$$1元\to 0元\to -1元\to 0元$$ 即，不存在经过 0 元的情况。0 元只能出现一次，而且是出现在终点。
2. 记酒鬼回到家的轨迹为序列
$$x_0,x_1,...,x_n,x_i≠x_n,i<n,x_n=家的位置坐标$$即强调，”酒鬼从 x 移到 y 处“指的是”酒鬼第一次碰到 y 处，即刻停止移步“，不存在比如$$x\to ...\to y\to ...\to y$$即强调 y 在轨迹中只能出现一次而且是在终点。

四、回答疑问

1. 根据上述1,2两点知道，输掉1元绝对不是输掉本局局，而是指过程
   $$x_0\to ...\to x_0-1,x_i≠x_0-1$$显然这个序列可以有无穷多种方式，进而知
   $$P(输掉1元)≠P(输掉本局)=p$$
2. 赌徒输光也绝不是连续输掉$x_0$局，而是指过程$$x_0\to ...\to x_n,x_i≠0,i<n,x_n=0$$显然这个序列也是有无穷多种，进而知$$P(赌徒输x_0元)≠P(赌徒连续输掉x_0局)=p^{x_0}$$

五、推出一些结论()

1. 根据以上几点，进一步可以得知，过程 A ：$x_0\to ...\to x_n$可以根据第一局输赢拆解为过程B：$x_0\to x_0-1\to ...\to x_n$和过程C： $x_0\to x_0+1\to ...\to x_n$，即如图
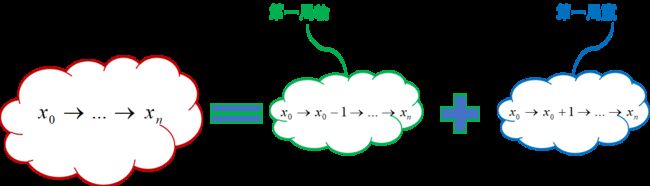
   进而概率上有，
   $$\begin{gathered} P(过程A)=P(过程B|第一局输)P(第一局输)+P(过程C|第一局赢)P(第一局赢) \\ =P(过程B|第一局输)p+P(过程C|第一局赢)(1-p) \end{gathered}$$
2. 赌徒输光 $x_0$ 元钱可以等价为赌徒输掉k 元达到 $x_0-k$这个状态，然后再从 $x_0-k$ 输光。即过程 A ：$x_0\to ...\to x_n$还可以拆解为过程B:$x_0\to ...\to x_0-k$ 然后紧接着过程C：$x_0-k\to ...\to x_n$

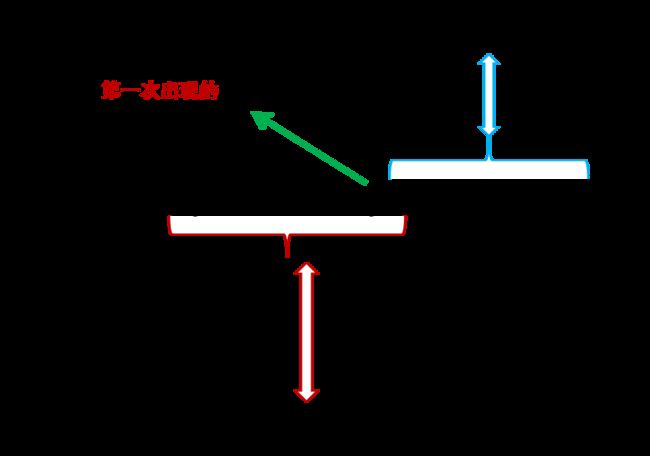
进而概率上有，
$$P(过程A)=P(过程B)P(过程C)$$ 进而当取 $x_n=0,k=x_0-1$时，$$过程A：x_0\to ...\to 0$$$$过程B：x_0\to ...\to x_0-k,即x_0\to ...\to 1$$$$过程C：1\to ...\to 0$$进而下式子恒成立，即$$P(x_0\to ...\to 0)=P(x_0\to ...\to 1)P(1\to ...\to 0)$$

六、正式解决问题

赌徒刚开始手里有 n 元钱，然后输光的概率记为 P(n)即对应于过程

$$x_0\to ...\to x_n，x_0=n,x_i≠0,i<n,x_n=0$$ 则根据前要第 5 点有

$$P(n)=P(n-1)p+P(n+1)(1-p)$$根据前要第 6 点又有

$$P(n)=P(n-1)P(1)$$又显然 P(0) = 1(即赌徒一开始手里就是0元，那直接就是输光，故而输光概率为 1)，进而
$$\begin{gathered} P(2)=P(2-1)P(1)=P(1{)}^2 \\ P(1)=P(0)p+P(2)(1-p)=p+P(2)(1-p) \end{gathered}$$结合两个式子得到$$P(1)=p+P(1{)}^2(1-p)$$这是一个一元二次方程，解得
$$P(1{)}_1=\frac{p}{1-p},P(1{)}_2=1(舍去)$$
进而
$$P(n)=P(n-1)P(1)=P(n-2)P(1{)}^2=...=P(1{)}^n={(\frac{p}{1-p})}^n$$