单调栈
给定两个没有重复元素的数组 nums1 和 nums2 ,其中nums1 是 nums2 的子集。找到 nums1 中每个元素在 nums2 中的下一个比其大的值。
nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在,对应位置输出-1。
示例 1:
输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
输出: [-1,3,-1]
解释:
对于num1中的数字4,你无法在第二个数组中找到下一个更大的数字,因此输出 -1。
对于num1中的数字1,第二个数组中数字1右边的下一个较大数字是 3。
对于num1中的数字2,第二个数组中没有下一个更大的数字,因此输出 -1。
示例 2:
输入: nums1 = [2,4], nums2 = [1,2,3,4].
输出: [3,-1]
解释:
对于num1中的数字2,第二个数组中的下一个较大数字是3。
对于num1中的数字4,第二个数组中没有下一个更大的数字,因此输出 -1。注意:
nums1和nums2中所有元素是唯一的。
nums1和nums2 的数组大小都不超过1000。
单调栈
栈(stack)是很简单的一种数据结构,先进后出的逻辑顺序,符合某些问题的特点,比如说函数调用栈。
单调栈实际上就是栈,只是利用了一些巧妙的逻辑,使得每次新元素入栈后,栈内的元素都保持有序(单调递增或单调递减)。
听起来有点像堆(heap)?不是的,单调栈用途不太广泛,只处理一种典型的问题,叫做 Next Greater Element。本文用讲解单调队列的算法模版解决这类问题。
这道题的暴力解法很好想到,就是对每个元素后面都进行扫描,找到第一个更大的元素就行了。但是暴力解法的时间复杂度是 O(n^2)。
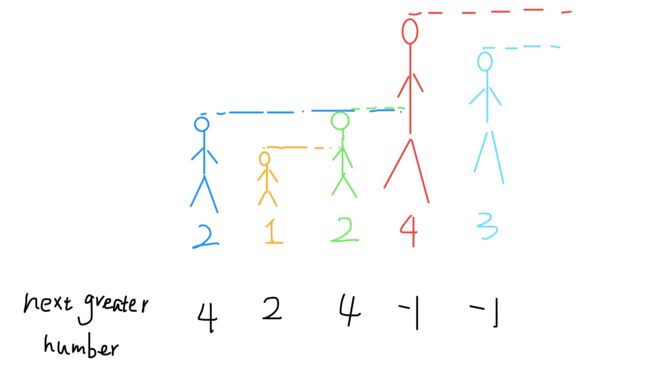
这个问题可以这样抽象思考:把数组的元素想象成并列站立的人,元素大小想象成人的身高。这些人面对你站成一列,如何求元素「2」的 Next Greater Number 呢?很简单,如果能够看到元素「2」,那么他后面可见的第一个人就是「2」的 Next Greater Number,因为比「2」小的元素身高不够,都被「2」挡住了,第一个露出来的就是答案。
这个情景很好理解吧?带着这个抽象的情景,先来看下代码。
vector nextGreaterElement(vector& nums) {
vector ans(nums.size()); // 存放答案的数组
stack s;
for (int i = nums.size() - 1; i >= 0; i--) { // 倒着往栈里放
while (!s.empty() && s.top() <= nums[i]) { // 判定个子高矮
s.pop(); // 矮个起开,反正也被挡着了。。。
}
ans[i] = s.empty() ? -1 : s.top(); // 这个元素身后的第一个高个
s.push(nums[i]); // 进队,接受之后的身高判定吧!
}
return ans;
} 这就是单调队列解决问题的模板。for 循环要从后往前扫描元素,因为我们借助的是栈的结构,倒着入栈,其实是正着出栈。while 循环是把两个“高个”元素之间的元素排除,因为他们的存在没有意义,前面挡着个“更高”的元素,所以他们不可能被作为后续进来的元素的 Next Great Number 了。
这个算法的时间复杂度不是那么直观,如果你看到 for 循环嵌套 while 循环,可能认为这个算法的复杂度也是 O(n^2),但是实际上这个算法的复杂度只有 O(n)。
分析它的时间复杂度,要从整体来看:总共有 n 个元素,每个元素都被 push 入栈了一次,而最多会被 pop 一次,没有任何冗余操作。所以总的计算规模是和元素规模 n 成正比的,也就是 O(n) 的复杂度。
解答上面的问题
class Solution {
public:
vector nextGreaterElement(vector& nums1, vector& nums2) {
map mp;
stack stack;
for(int value : nums1) {
mp[value] = -1;
}
for(int i=0; i 每日温度
给你一个数组 T = [73, 74, 75, 71, 69, 72, 76, 73],这个数组存放的是近几天的天气气温(这气温这么高?不是的,这里用的华氏度)。你返回一个数组,计算:对于每一天,你还要至少等多少天才能等到一个更暖和的气温;如果等不到那一天,填 0 。
举例:给你 T = [73, 74, 75, 71, 69, 72, 76, 73],你返回 [1, 1, 4, 2, 1, 1, 0, 0]。
解释:第一天 73 华氏度,第二天 74 华氏度,比 73 大,所以对于第一天,只要等一天就能等到一个更暖和的气温。后面的同理。
你已经对 Next Greater Number 类型问题有些敏感了,这个问题本质上也是找 Next Greater Number,只不过现在不是问你 Next Greater Number 是多少,而是问你当前距离 Next Greater Number 的距离而已。
相同类型的问题,相同的思路,直接调用单调栈的算法模板,稍作改动就可以啦,直接上代码把。
vector dailyTemperatures(vector& T) {
vector ans(T.size());
stack s; // 这里放元素索引,而不是元素
for (int i = T.size() - 1; i >= 0; i--) {
while (!s.empty() && T[s.top()] <= T[i]) {
s.pop();
}
ans[i] = s.empty() ? 0 : (s.top() - i); // 得到索引间距
s.push(i); // 加入索引,而不是元素
}
return ans;
}