Leetcode题解---“滑动窗口法”解题
目录
3. 无重复字符的最长子串
76. 最小覆盖子串
159. 至多包含两个不同字符的最长子串
340. 至多包含 K 个不同字符的最长子串
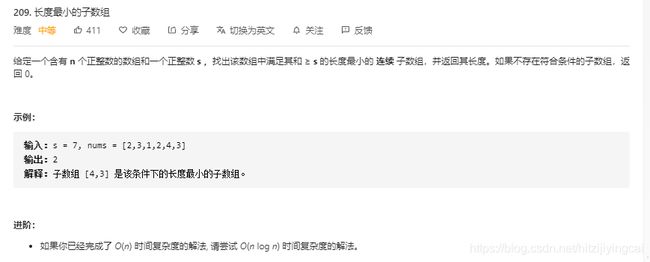
209. 长度最小的子数组
567. 字符串的排列
632. 最小区间
727. 最小窗口子序列
904. 水果成篮
930. 和相同的二元子数组
992. K 个不同整数的子数组
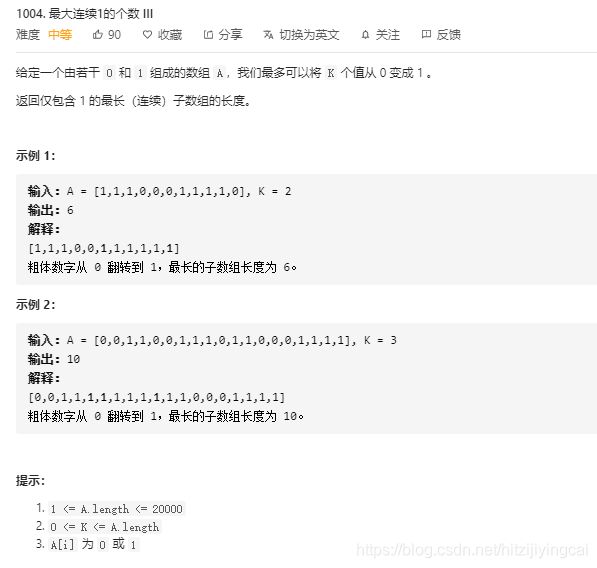
1004. 最大连续1的个数 III
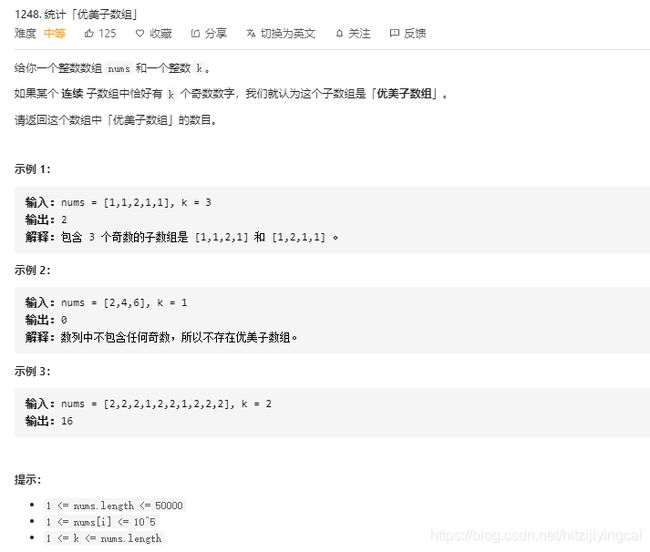
1248. 统计「优美子数组」
具体为:
3. 无重复字符的最长子串
![]()
解题思路:双指针+滑动窗口
假设原始字符串S如下
![]()
从左侧开始遍历S,以i标记窗口左侧,j标记窗口右侧,初始时,i=0,j=0,即开头a所在的位置,此时,窗口大小为1
然后,将j右移,逐步扩大窗口,依次经过b、c、d,此时,窗口内均无重复字符,继续右移j
![]()
当j移动到d后面的a所在位置时,对应字符a在窗口中已存在,此时,窗口大小为5,去除当前重复的一位,窗口大小为4。此时窗口内的字符串abcd为
![]()
找到窗口中已存在的该字符所在位置,并将i移动到该位置下一位
![]()
此时为第二个窗口
![]()
继续重复之前的操作,直到j移动到字符串最后一位停止。
代码:
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
length = 0
mark = set() # 用集合标明是否有出现重复字母
r = 0 # 右指针
for i in range(len(s)):
if i != 0:
mark.remove(s[i - 1])
while r < len(s) and s[r] not in mark: # 如果不满足条件说明r走到了s的尽头或r指向的元素
mark.add(s[r]) # 将当前r指向的字母加入集合
r += 1
length = max(length, r - i) # 在每一个位置更新最大值
return length
下面介绍关于滑动窗口的万能模板,可以解决相关问题:
class Solution:
def lengthOfLongestSubstring(self, s):
"""
:type s: str
:rtype: int
"""
from collections import defaultdict
lookup = defaultdict(int)
start = 0
end = 0
max_len = 0
counter = 0
while end < len(s):
if lookup[s[end]] > 0:
counter += 1
lookup[s[end]] += 1
end += 1
while counter > 0:
if lookup[s[start]] > 1:
counter -= 1
lookup[s[start]] -= 1
start += 1
max_len = max(max_len, end - start)
return max_len
76. 最小覆盖子串
class Solution:
def minWindow(self, s: str, t: str) -> str:
from collections import defaultdict
lookup = defaultdict(int)
for c in t:
lookup[c] += 1
start = 0
end = 0
min_len = float("inf")
counter = len(t)
res = ""
while end < len(s):
if lookup[s[end]] > 0:
counter -= 1
lookup[s[end]] -= 1
end += 1
while counter == 0:
if min_len > end - start:
min_len = end - start
res = s[start:end]
if lookup[s[start]] == 0:
counter += 1
lookup[s[start]] += 1
start += 1
return res159. 至多包含两个不同字符的最长子串
class Solution:
def lengthOfLongestSubstringTwoDistinct(self, s: str) -> int:
from collections import defaultdict
lookup = defaultdict(int)
start = 0
end = 0
max_len = 0
counter = 0
while end < len(s):
if lookup[s[end]] == 0:
counter += 1
lookup[s[end]] += 1
end +=1
while counter > 2:
if lookup[s[start]] == 1:
counter -= 1
lookup[s[start]] -= 1
start += 1
max_len = max(max_len, end - start)
return max_len
class Solution {
public:
int lengthOfLongestSubstringTwoDistinct(string s) {
unordered_map hashmap;
int res = 0;
for(int i=0,j=0;j2){
if(hashmap[s[i]]>1) hashmap[s[i]]--;
else if(hashmap[s[i]]==1) hashmap.erase(s[i]);
i++;
}
res = max(res,j-i+1);
}
return res;
}
}; 340. 至多包含 K 个不同字符的最长子串
class Solution:
def lengthOfLongestSubstringKDistinct(self, s: str, k: int) -> int:
from collections import defaultdict
lookup = defaultdict(int)
start = 0
end = 0
max_len = 0
counter = 0
while end < len(s):
if lookup[s[end]] == 0:
counter += 1
lookup[s[end]] += 1
end += 1
while counter > k:
if lookup[s[start]] == 1:
counter -= 1
lookup[s[start]] -= 1
start += 1
max_len = max(max_len, end - start)
return max_len
class Solution {
public int lengthOfLongestSubstringKDistinct(String s, int k) {
Set set =new HashSet<>();
int res = 0;
for(int i = 0;i 209. 长度最小的子数组
567. 字符串的排列
632. 最小区间
排序滑窗:
class Solution:
def smallestRange(self, nums: List[List[int]]) -> List[int]:
lst = []
for i in range(len(nums)):
for j in range(len(nums[i])):
lst.append((nums[i][j],i))
lst.sort(key=lambda x:x[0])
i = 0,k = 0
ans = [-10**9, 10**9]
count = {}
for j in range(len(lst)):
if lst[j][1] not in count.keys():
k+=1
count[lst[j][1]] = 1
else:
count[lst[j][1]] += 1
if k==len(nums):
while count[lst[i][1]]>1:
count[lst[i][1]] -= 1
i += 1
if ans[1]-ans[0]>lst[j][0]-lst[i][0]:
ans[1],ans[0] = lst[j][0],lst[i][0]
return ans堆:
class Solution:
def smallestRange(self, nums):
from heapq import heappush, heappop
k = len(nums)
heap = []
tmpmax=-1000000
for i in range(k):
heappush(heap, [nums[i][0], i, 0])
tmpmax=max(tmpmax, nums[i][0])
ans=[]
while True:
cur=heappop(heap)
cand=[cur[0], tmpmax]
if not len(ans) or (cand[1]-cand[0]=len(nums[idx]):
break
new_insert=nums[idx][pt+1]
tmpmax=max(tmpmax, new_insert)
heappush(heap, [new_insert, idx, pt+1])
return ans 727. 最小窗口子序列
class Solution {
public:
string minWindow(string S, string T) {
int i = 0, j = 0, minlen = INT_MAX;
int l = -1, r;
while(i < S.size())
{
if(S[i] == T[j])
{
j++;
if(j == T.size())//全部匹配了
{
r = i+1;
j--;
while(j >= 0)
{
while(S[i] != T[j])//向左匹配
i--;
i--;j--;
}
i++,j++;
if(r-i < minlen)
{
minlen = r - i;
l = i;
}
}
}
i++;
}
return l == -1 ? "" : S.substr(l,minlen);
}
};
904. 水果成篮
930. 和相同的二元子数组
992. K 个不同整数的子数组
1004. 最大连续1的个数 III
1248. 统计「优美子数组」