数据结构·分块（入门例题·算法分析说明·代码编写指导·参考模板）（未完待续）

一、分块思想简介

对一个非常大的数组作大量操作时，可以尝试将其分成若干个子块，然后对每块整体处理，以大量减少操作的总次数，防止TLE。

常见名词解释
区间：数列中连续一段的元素
区间操作：将某个区间[a,b]的所有元素进行的操作（求和、加减等）
块：我们将数列划分成若干个不重叠的连续区间，每个区间称为一个块
整块：在一个区间操作时，完整包含于区间的块
不完整的块：在一个区间操作时，只有部分包含于区间的块，这些块一般都是区间左右端点所在的两个块

目前，本博客的部分内容是根据 http://hzwer.com/8053.html 中的题目和除代码以外的部分改编的，额外增加的内容是算法解析与代码编写指导，同时提供通用性更高的算法模板。这里的通用性指的是：面对不同的竞赛题目也可以在套用模板时尽可能少作改动或不作改动、只需简单调用模板函数而无需过多的额外操作就能完成主算法。

二、例题

1、LOJ #6277 https://loj.ac/problem/6277
已知数列 {an} 的长为 n ，以及 n 个操作。
输入包含一个整数 n 和下一行 n 个数，代表数列的每一项（从 1 开始编号）。
接下来 n 行，每行 4 个数 o、l、r、c。
o 只能取 0 或 1 ，当 o = 0 时，对数列 {an} 的离散闭区间 [l, r] 的每一项都增加 c 。当 o = 1 时，给出项 ar 的值，输入中的 l 、c 直接忽略。

解 如果我们把每
m 个元素分为一块，共有 n/m 块，每次区间加的操作会涉及 O(n/m) 个整块，以及区间两侧两个不完整的块中的少于 2m 个元素。
在原数列 {an} 输入完毕后，将数据分块并将需要的刻画整块的某个特征的数据存入另外一个数组 {sn} 中。需要对某区间求解时，将中间完整的块利用刚才额外保存的数据整体处理，然后将两端不完整的块暴力运算再与先前结果作相应处理即为最终答案。
这样每次第0类操作的复杂度是O(n/m) + O(m)，由时间复杂度的定义易得：总操作数为

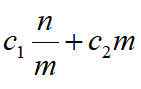
c1、c2是常数。根据基本不等式，当

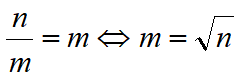
时，操作次数最少。所以分块时我们尽量让每个块的大小接近根号 n 。
先对数列进行分块，一个分块对应一个新的数组 {sn} 的每一个值（累加标记），一开始都设为零。每次第 0 类操作都对所有完整分块对应的累加标记加上 c 。询问某项的值的时候，需要输出该项的原始值与所在分块的累加值的和。
对第1类操作，直接输出相应的值即可。
这里将数列分成 ceil(sqrt(n)) 块，最后一个块可能不是完整的。每个块对应一个值，用于记录该块的累加值。
然后当 o = 0 时，对 l 和 r 所在区间的中间区间（都是完整区间）的累加值都加上 c 。对于 l 和 r 所在的区间与 [l, r] 的交集，可以验证，无论 l 和 r 是否落在端点处，都可直接将原数列 {an} 中在交集的范围内的每个值都加上 c ，无需额外讨论。
具体来说，记

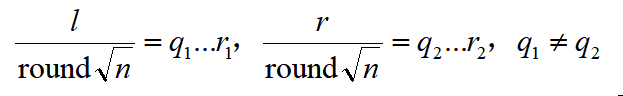
完整区间的下标是 q1 + 1 到 q2 - 1 ，对数列 {tn} 的这部分下标对应的项都加上 c 即可，然后再对 l 和 r 所在的区间与 [l, r] 的交集这部分进行处理。
如果 l 与 r 在同一个区间，即 q1 = q2 ，此时对这个交集就需要单独处理：直接对 a[l] 到 a[r] 都加 c 。否则，对 a[l] 到 a[(q1 + 1)round(根号n) - 1] 和 a[q2 * round(根号n)] 到 a[r] 的每一项都加上 c 。这一步可以通过在草稿纸上画示意图直接写出。
需要输出某项的值的时候，先查询该项所在区间的总体的累加值，再加上原数列中的值，然后输出。

AC 代码（336 ms）：

#include
#include
#include
#pragma warning(disable:4996)
int a[50000], s[230], c; unsigned short m, n, l, r; unsigned char o;
inline unsigned short block_reset_add_sign(const unsigned short& n, const int* arr, int* blk_sign) {
	const unsigned short bm = ceil(sqrt(n)); for (unsigned short i = 0; i < bm; ++i)blk_sign[i] = 0;
	return bm;
}
inline void add(int* arr, int* blk_sign, const int& val_to_add, const unsigned short& num_blk, const unsigned short& l, const unsigned short& r) {
	unsigned short q1, r1, q2, r2, end1, begin2;
	q1 = l / num_blk, r1 = l - q1 * num_blk, q2 = r / num_blk, r2 = l - q2 * num_blk;
	for (unsigned short i = q1 + 1; i < q2; ++i)blk_sign[i] += val_to_add;
	switch (q1 != q2) {
	case true:
		end1 = (q1 + 1) * num_blk - 1; for (unsigned short i = l; i <= end1; ++i)arr[i] += val_to_add;
		begin2 = q2 * num_blk; for (unsigned short i = begin2; i <= r; ++i)arr[i] += val_to_add;
		break;
	case false:for (unsigned short i = l; i <= r; ++i)arr[i] += val_to_add;
	}
}
inline int get_add_sign(const int* arr, const unsigned short& num_blk, const int* sign, const unsigned short& index) {
	return sign[index / num_blk];
}
int main() {
	scanf("%hu", &n);
	for (unsigned short i = 0; i < n; ++i)scanf("%d", &a[i]);
	m = block_reset_add_sign(n, a, s);
	for (unsigned short i = 0; i < n; ++i) {
		scanf("%hhu%hu%hu%d", &o, &l, &r, &c); --l, --r;
		switch (o) {
		case 0:add(a, s, c, m, l, r); break;
		case 1:printf("%d\n", a[r] + get_add_sign(a, m, s, r));
		}
	}
	return 0;
}

（上文给出的例题来源中，原作者给的代码采用了快读，因此比这份代码跑得快）