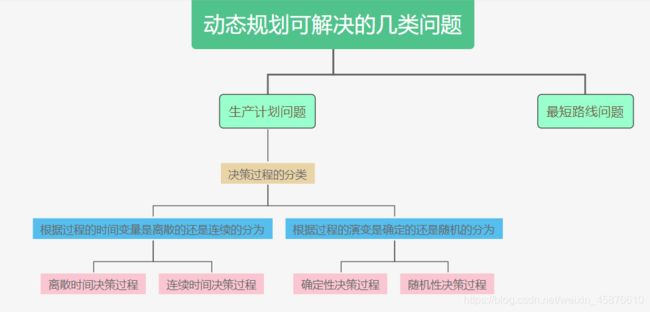
动态规划------求解决策过程中最优化的数学方法
文章目录
- 一、常规优化模型的种类
- 二、常规优化模型的知识及应用（2）------非线性规划
-
- 2.1简介
- 2.2动态规划相关问题的求解
-
- 2.2.1求解最短路径问题（lingo软件求解）
- 2.2.2典型问题的动态规划模型
一、常规优化模型的种类
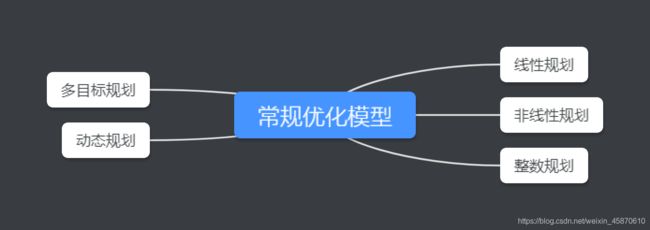
本人已经发布过线性规划算法和非线性规划算法的相关知识的博客，有需要了解的同学请移步
线性规划------单纯形法真的难~~~
数学模型之非线性规划------脑细胞不够用了~~~
二、常规优化模型的知识及应用（2）------非线性规划
2.1简介
动态规划主要用于求解以时间划分阶段的动态过程的优化问题
2.2动态规划相关问题的求解
2.2.1求解最短路径问题（lingo软件求解）
lingo的代码如下：
model:
Title Dynamic Programming;
sets:
vertex/A,B1,B2,C1,C2,C3,C4,D1,D2,D3,E1,E2,E3,F1,F2,G/:L;
road(vertex,vertex)/A B1,A B2,B1 C1,B1 C2,B1 c3,B2 C2,B2 C3,B2 C4,
C1 D1,C1 D2,C2 D1,C2 D2,C3 D2,C3 D3,C4 D2,C4 D3,
D1 E1,D1 E2,D2 E2,D2 E3,D3 E2,D3 E3,
E1 F1,E1 F2,E2 F1,E2 F2,E3 F1,E3 F2,F1 G,F2 G/:D;
endsets
data:
D=5 3 1 3 6 8 7 6
6 8 3 5 3 3 8 4
2 2 1 2 3 3
3 5 5 2 6 6 4 3;
L=0,,,,,,,,,,,,,,,;
enddata
@for(vertex(i)|i#GT#1:L(i)=@min(road(j,i):L(j)+D(j,i)));
end
2.2.2典型问题的动态规划模型
