Multi-scale Features for Approximate Alignment of Point-based Surfaces论文阅读
问题
给定一个点云描述( P = { ( p i , n i ) } i ∈ I \mathcal{P}=\{(\mathbf{p}_{i}, \mathbf{n}_{i})\}_{i \in \mathcal{I}} P={ (pi,ni)}i∈I,其中 p i \mathbf{p}_i pi是点的位置, n i \mathbf{n}_{i} ni是点的法向, I \mathcal{I} I是点的集合)的曲面(surfel cloud),求曲面特征。
基本思路
先对曲面做不同尺度的smooth(类似于图像处理中的高斯金字塔),然后仿照二维图像中求SIFT特征的方法计算特征。
点云Smooth
假设给定点云 P = { ( p i , n i ) } i ∈ I \mathcal{P}=\{(\mathbf{p}_{i}, \mathbf{n}_{i})\}_{i \in \mathcal{I}} P={ (pi,ni)}i∈I以及任意一个三维空间的点 x \mathbf{x} x,计算 x \mathbf{x} x在 P \mathcal{P} P上的投影。
因为是三维空间中任意一点,因此我们往往要将它表示成已知的各点的加权平均。如果按照高斯函数的范围取权重,则 x \mathbf{x} x相对于某一点 p i \mathbf{p}_{i} pi的权重为
θ i h ( x ) : = A i e − d 2 ( x , p i ) / h 2 ∑ j ∈ I A j e − d 2 ( x , p j ) / h 2 \theta_{i}^{h}(\mathbf{x}):=\frac{A_{i} e^{-d^{2}\left(\mathbf{x}, \mathbf{p}_{i}\right) / h^{2}}}{\sum_{j \in \mathcal{I}} A_{j} e^{-d^{2}\left(\mathbf{x}, \mathbf{p}_{j}\right) / h^{2}}} θih(x):=∑j∈IAje−d2(x,pj)/h2Aie−d2(x,pi)/h2
其中, d ( x , p i ) d(\mathbf{x}, \mathbf{p}_i) d(x,pi)表示两点之间的距离, h h h表示高斯函数的方差(半径), A i A_i Ai表示各点的面积——如果我们知道各点的连接方式,那么面积就是一环三角形面的面积的三分之一;如果我们只知道点云,不知道连接方式,则 A i A_i Ai统一等于1。
使用权重加权,我们可以计算得到 x \mathbf{x} x的法向:
n [ P , h ] ( x ) : = ∑ i ∈ I θ i h ( x ) n i \mathbf{n}_{[\mathcal{P}, h]}(\mathbf{x}):=\sum_{i \in \mathcal{I}} \theta_{i}^{h}(\mathbf{x}) \mathbf{n}_{i} n[P,h](x):=i∈I∑θih(x)ni
因此,如果我们想计算 x \mathbf{x} x在曲面上的投影,则可以求以下式子的最小值:
E [ P , h ] ( x ) : = ∑ i ∈ I θ i h ( x ) ⟨ n [ P , h ] ( x ) , x − p i ⟩ 2 E_{[\mathcal{P}, h]}(\mathbf{x}):=\sum_{i \in \mathcal{I}} \theta_{i}^{h}(\mathbf{x})\left\langle\mathbf{n}_{[\mathcal{P}, h]}(\mathbf{x}), \mathbf{x}-\mathbf{p}_{i}\right\rangle^{2} E[P,h](x):=i∈I∑θih(x)⟨n[P,h](x),x−pi⟩2
显然,只有 x \mathbf{x} x在曲面上时,首先 x − p i \mathbf{x}-\mathbf{p}_i x−pi的值较小,其次它们往往和法向 n [ P , h ] ( x ) \mathbf{n}_{[\mathcal{P}, h]}(\mathbf{x}) n[P,h](x)垂直,因此能让误差取到最小值。曲线内外的点,通过迭代求解,就可以投影到曲面上。
对于点云的Smooth,我们将每个点自身带入到上面的计算中,每个点的位置都受到周围点位置的影响,相当于进行了smooth。我们取不同的 h h h半径,即 h j = h 0 F j h_{j}=h_{0} F^{j} hj=h0Fj,其中 F F F是一个可调常数(文中设置为 2 1 / 4 2^{1/4} 21/4),就得到了不同程度的smooth,与图像处理中的高斯金字塔十分类似。
特征计算
我们希望特征是不变量在邻域中的最大值,因此首先定义邻域。对于空间上的一个点 q \mathbf{q} q,我们认为以下集合中的点在 q \mathbf{q} q的邻域内: b ( q , R ) : = { k ∈ I : d ( p k , q ) < R } b(\mathbf{q}, R):=\left\{k \in \mathcal{I}: d\left(\mathbf{p}_{k}, \mathbf{q}\right)
然后我们定义不变量。有了不同尺度的高斯滤波后(即 P j : = { ( p i h j , n i h j ) } i ∈ I \mathcal{P}_{j}:=\{(\mathbf{p}_{i}^{h_{j}}, \mathbf{n}_{i}^{h_{j}})\}_{i \in \mathcal{I}} Pj:={ (pihj,nihj)}i∈I),我们对他们相邻两层计算
d j ( i ) : = ⟨ n i j , p i j − p i j − 1 ⟩ d_{j}(i):=\left\langle\mathbf{n}_{i}^{j}, \mathbf{p}_{i}^{j}-\mathbf{p}_{i}^{j-1}\right\rangle dj(i):=⟨nij,pij−pij−1⟩
然后仿照SIFT,使用 d j ( i ) d_{j}(i) dj(i)来定义特征:
d j ( i ) > d j − 1 ( i ′ ) for all i ′ ∈ b ( p i , C h j − 1 ) d j ( i ) > d j ( i ′ ) for all i ′ ∈ b ( p i , C h j ) \ { i } d j ( i ) > d j + 1 ( i ′ ) for all i ′ ∈ b ( p i , C h j + 1 ) \begin{aligned} &d_{j}(i)>d_{j-1}\left(i^{\prime}\right) \quad \text { for all } i^{\prime} \in b\left(p_{i}, C h_{j-1}\right)\\ &d_{j}(i)>d_{j}\left(i^{\prime}\right) \quad \text { for all } i^{\prime} \in b\left(p_{i}, C h_{j}\right) \backslash\{i\}\\ &d_{j}(i)>d_{j+1}\left(i^{\prime}\right) \quad \text { for all } i^{\prime} \in b\left(p_{i}, C h_{j+1}\right) \end{aligned} dj(i)>dj−1(i′) for all i′∈b(pi,Chj−1)dj(i)>dj(i′) for all i′∈b(pi,Chj)\{ i}dj(i)>dj+1(i′) for all i′∈b(pi,Chj+1)
特征点的 d j ( i ) d_{j}(i) dj(i)需比同一层、上一层、下一层的邻域内的其他点的 d j ( i ) d_{j}(i) dj(i)都要大。类似地,我们也可以按照最小值给出一个特征的定义。
稳定性分析
稳定性分析主要考虑三个因素:均匀重采样、添加噪声、使用QSlim模型简化(可参考我的另一篇博客对QSlim的介绍)对特征点的影响。
首先我们需要定义如何判定两个(稍有不同的)模型上特征点是否一致。文中的判定方法是,对于 x \mathbf{x} x点,尺度为 h h h的特征 f f f,如果在另一个模型的相同尺度或邻近尺度 h ′ h' h′(对于本文中, h ′ ∈ [ F − 1 h , F h ] h'\in[F^{-1}h,Fh] h′∈[F−1h,Fh]),存在一个特征 f ′ f' f′,它的坐标 x ′ \mathbf{x'} x′与 x \mathbf{x} x之间的距离小于 h 2 \frac{h}{2} 2h,我们就判定 f f f与 f ′ f' f′之间存在对应关系。
文中测试了Venus、Buddha和Bunny三个模型,对均匀重采样、添加噪声,得到了Figure1。
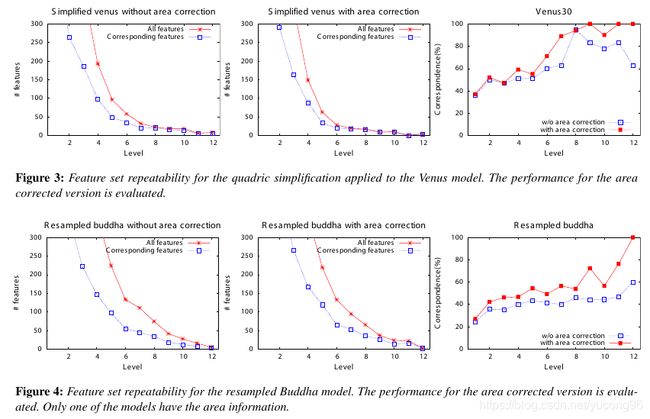
对模型简化,得到了Figure4。同时,在模型简化中,引入了面积权重,发现带面积权重的比不带面积权重的要好。
我个人感觉,这里的稳定性看起来一般,只有约一半的点找到了对应点。不知道其他特征算法的稳定性和它相比如何。
表面局部特征描述子
上面的方法只是找到了特征点的位置,但没有特征点的描述子。如果我们把那些坐标、法向、尺度之类的视为描述子,那么它们就不具有旋转不变性了。因此,要仿造SIFT就要仿到底,我们要加上邻域的信息,形成直方统计,然后再加一个傅里叶变换。
具体来说,我们在特征点和法向垂直的方向,取一个平面,对平面上以特征点为中心,按圆盘采样,如下图所示:

如果我们在平面上定义uv坐标系,则每个点 ξ k l \xi_{k l} ξkl的位置为
ξ k l : = x + 2 l h M ( cos ( 2 π k N ) u + sin ( 2 π k N ) v ) \xi_{k l}:=\mathbf{x}+\frac{2 l h}{M}\left(\cos \left(\frac{2 \pi k}{N}\right) \mathbf{u}+\sin \left(\frac{2 \pi k}{N}\right) \mathbf{v}\right) ξkl:=x+M2lh(cos(N2πk)u+sin(N2πk)v)
其中 l = 1 , ⋯ , M l=1,\cdots,M l=1,⋯,M,为在半径上采样, k = 1 , ⋯ , N k=1,\cdots,N k=1,⋯,N,为在角度上采样。对于这样一个点 ξ k l \xi_{k l} ξkl,我们也可以加权地求它的法向 v k l v_{k l} vkl,即
v k l = n [ P , h ] ( ξ k l ) v_{k l}=\mathbf{n}_{[P, h]}\left(\xi_{k l}\right) vkl=n[P,h](ξkl)
类似上面对于不变量的定义,这里也对每个点求不变量 s k l s_{k l} skl:
s k l = ⟨ ξ k l − x , v k l ⟩ ∥ ξ k l − x ∥ s_{k l}=\frac{\left\langle\xi_{k l}-\mathbf{x}, \mathbf{v}_{k l}\right\rangle}{\left\|\xi_{k l}-\mathbf{x}\right\|} skl=∥ξkl−x∥⟨ξkl−x,vkl⟩
对这些 s k l s_{k l} skl做直方统计就好了。但另一种更好的方法是,通过傅里叶变换实现空间压缩和特征保留的方法,在 l l l方向做离散余弦变换(DCT),在 k k k方向做离散傅里叶变换(DFT),然后取结果的左上角 M ′ × N ′ M'×N' M′×N′个值就好了。因此,它的特征描述子为:
σ P ( x , n , h ) : = ( s ~ k l ) k = 1 , … N ′ , l = 1 , … M ′ \sigma_{P}(\mathbf{x}, \mathbf{n}, h):=\left(\tilde{s}_{k l}\right)_{k=1, \ldots N^{\prime}, l=1, \ldots M^{\prime}} σP(x,n,h):=(s~kl)k=1,…N′,l=1,…M′
稳定性分析
由于我们在点的切平面上对圆盘进行采样,这些采样点都没有落在模型表面。实验发现,落在表面反而由于表面的噪声,导致结果更差。Figure6中,左图使用投影落在模型表面,右图直接使用切平面,比较两者和不加噪声的模型之间的误差。发现左图误差更大。

特征过滤
另外,如果在一个平面上加噪声,平面会变得起伏不平,从而出现许多小的特征。但这些特征在描述子的大小(magnitude)上往往很小,因此可以人为设定阈值将其去除。
应用:表面匹配
过程略。放一张结果图吧(Figure10)。
参考文献
Li, Xinju, and Igor Guskov. “Multiscale Features for Approximate Alignment of Point-based Surfaces.” Symposium on geometry processing. Vol. 255. 2005.