BP神经网络的工程应用

<>

一.BP网络在函数逼近中的应用

例1.要求设计一个BP网络,逼近以下函数:g(x) = 1+sin(k·pi/2·x),实现对该非线性函数的逼近.其中,分别令k=2,3,6进行仿真,通过调节参数得到信号的频率与隐含层节点之间、隐含层节点与函数逼近能力之间的关系.

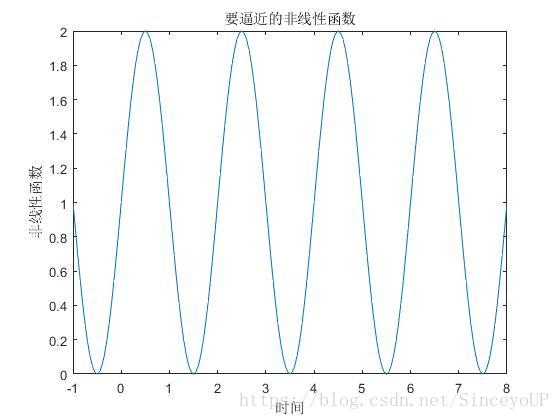
解:假设频率参数k=2,绘制要逼近的非线性函数的目标函数.MATLAB代码如下.

k=2;
p=[-1:0.05:8];
t = 1+sin(k*pi/2*p);
plot(p,t,'-');
title('要逼近的非线性函数');
xlabel('时间');
ylabel('非线性函数');

得到目标曲线函数图像.

用newff()函数创建BP网络结构.隐含层神经元数目n可以改变,暂设n=5,输出层有一个神经元.选择隐含层和输出层神经元传递函数分别用tansig函数和purelin函数,网络训练的算法采用Levenberg-Marquardt算法trainlm.

clc;clear;
k=2;
p=[-1:0.05:8];
t = 1+sin(k*pi/2*p);
% plot(p,t,'-');
% title('要逼近的非线性函数');
% xlabel('时间');
% ylabel('非线性函数');
n=5;
net = newff(minmax(p),[n,1],{'tansig' 'purelin'},'trainlm');
%[n,1]分别为隐含层和输出层神经元数目,tansig,purelin分别为隐含层和输出层神经元传递函数
%网络训练的算法采用Levenberg-Marquardt算法trainlm
%对于初始网络,可以应用sim()函数观察网络输出.
y1=sim(net,p);
figure;
plot(p,t,'-',p,y1,':');
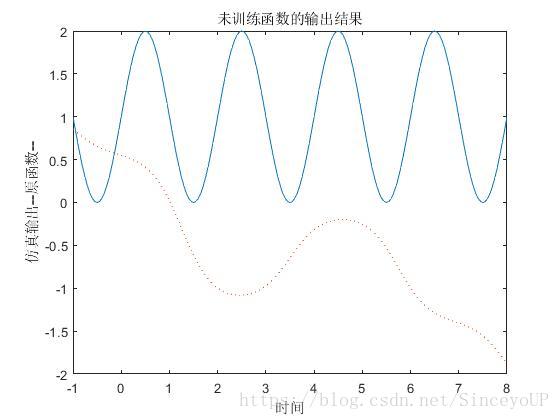
title('未训练函数的输出结果');
xlabel('时间');
ylabel('仿真输出--原函数--');

运行上述代码得到网络输出曲线与原函数的比较图

       因为使用newff()函数建立函数网络时,权值与和阈值的初始化时随机的,所以网络输出结构很差,根本达不到函数逼近的目的,每次运行的结果也有时不同.

       应用train()函数对网络进行训练之前,需要预先设置网络训练参数.将训练时间设置为200,训练精度设置为0.2,其余参数使用缺省值.训练神经网络的MATLAB代码如下所示.

net.trainParam.epochs=200;%网络训练时间设置为200
net.trainParam.goal=0.2;  %网络训练精度设置为0.2
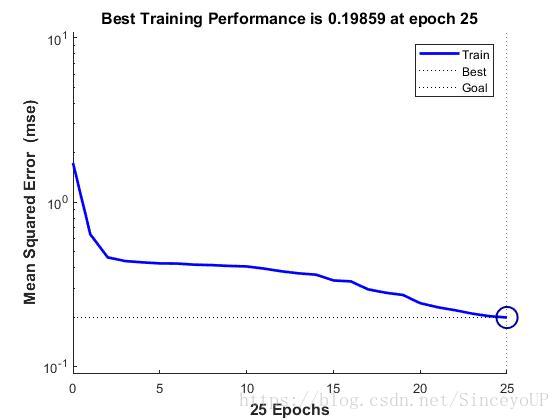
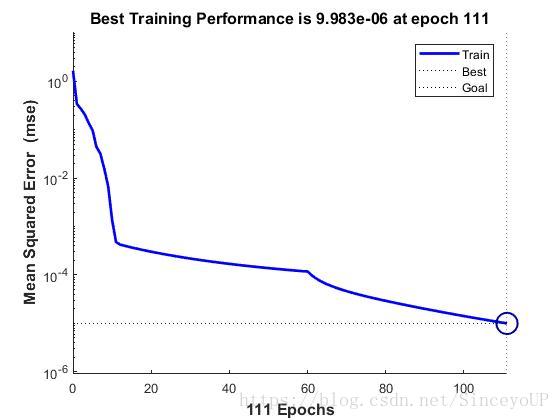
net=train(net,p,t);       %开始训练网格

训练后得到的误差变化过程如图所示.从图中可以看出,神经网络运行25步后,网络输出误差达到设定的训练精度.

(这里我自己使用时发现每次学习时间都不一样,可能是因为神经网络在创建时候权值和阈值都是随机的,存在有的情况可以在较少的学习时间内达到设定的训练精度)

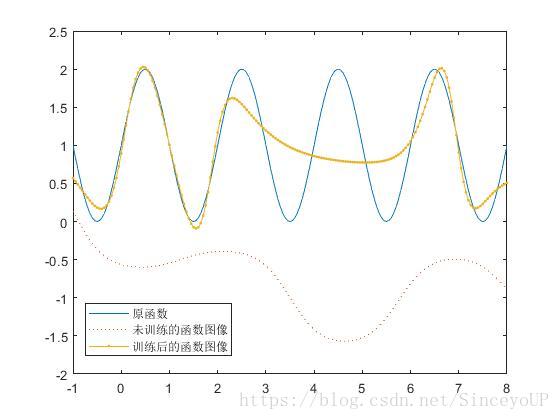
对于训练好的网络进行仿真.

       从图中可以看出,相比没有训练的曲线,经过训练之后的曲线和原始的目标曲线更接近.这说明经过训练后,BP网络对非线性函数的逼近效果比较好.

       改变非线性函数的频率和BP函数隐含层神经元的数目,对于函数的逼近效果有一定的影响.

       网络非线性程越高,对于BP网络的要求越高,则相同的网络逼近效果要差一些;隐含层神经元的数目对于网络逼近效果也有一定影响,一般来说隐含层神经元数目越多,则BP网络逼近非线性函数的能力越强.

       下面通过改变频率参数和非线性函数的隐含层神经元数目来加以比较证明.

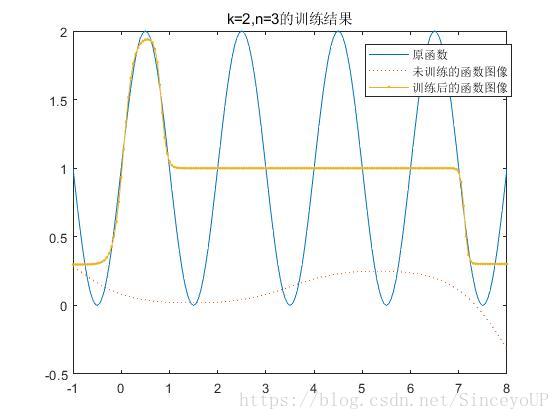
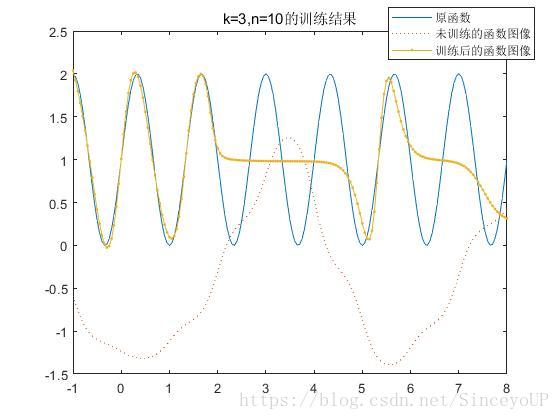
       (1)频率参数设为k=2,当隐含层神经元数目分别取n=3,n=10时,得到训练后的网络输出结果.

       从图中可以看出,当n=10时,经过训练后的曲线基本与目标曲线重合;当n=3时,经过训练后的曲线基本不跟目标曲线重合.这说明增加隐含层的神经元个数可以增加BP神经网络预测的准确性.

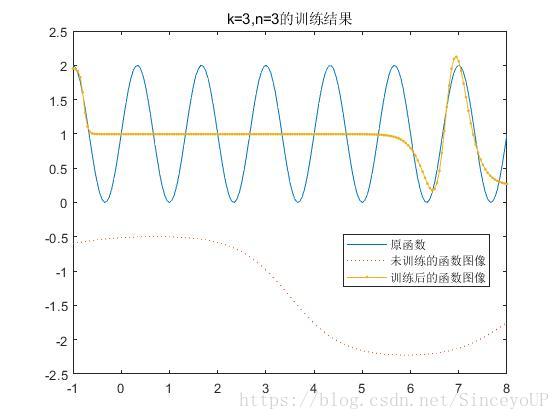
       (2)频率参数设为3,当隐含层神经元数目分别取n=3,n=10时,得到训练后的网络输出结果.

       由此可见,n取不同的值对函数逼近的效果有很大的影响.改变BP网络隐含层神经元的数目,可以改变BP神经网络对于函数的逼近效果.隐含层神经元数目越多,则BP网络逼近非线性函数的能力越强.

       由于单隐含层的BP神经网络可以逼近任意的非线性映射,在隐含层的神经元个数可以随意调整的前提下.输入层和输出层的神经元个数为1,只有一个隐含层,其个数根据上述的设计经验公式和本例的实际情况,选取9~16之间.

       通过下面的通用的MATLAB的程序段,更换不同的学习方法,得到的误差曲线和训练后网格仿真输出结果.

clc;clear;
x=-4:0.01:4;
t = sin(pi*x)+sin(pi/2*x);
n=15;
net = newff(minmax(x),[1,n,1],{'tansig','tansig','purelin'},'trainlm');
figure;
y1=sim(net,x);
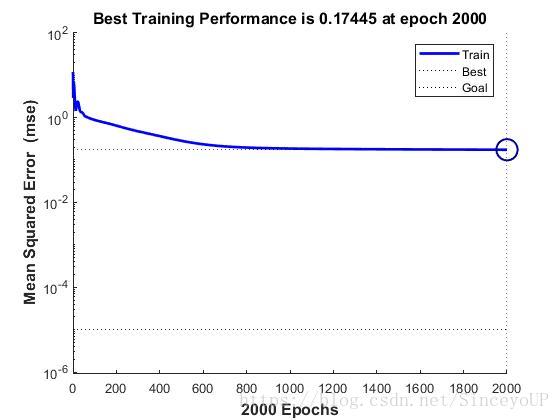
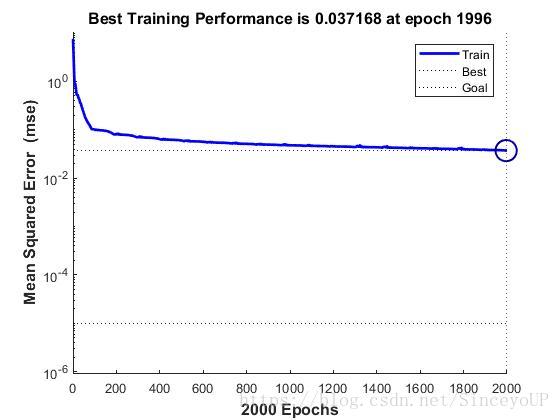
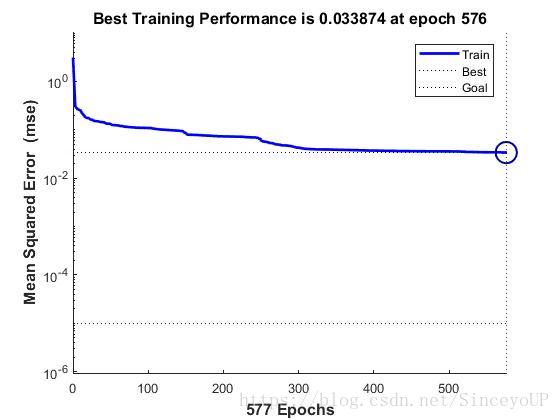
net.trainParam.epochs=2000;%网络训练时间设置为200
net.trainParam.goal=0.00001; %网络训练精度设置为0.2
net=train(net,x,t);       %开始训练网格
y2=sim(net,x);
err=y2-t;                 %求欧几里得范数,也就是求欧式距离
res=norm(err);
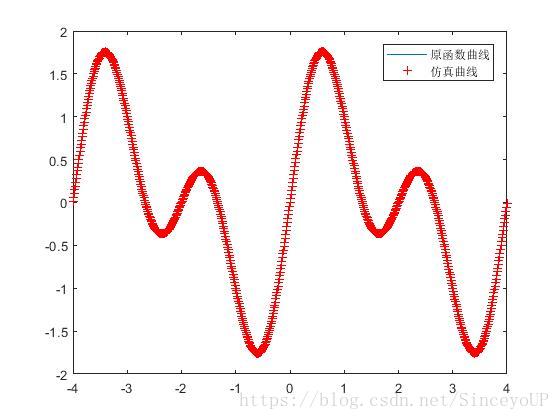
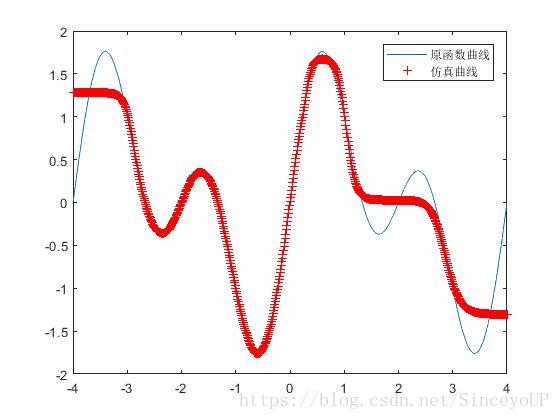
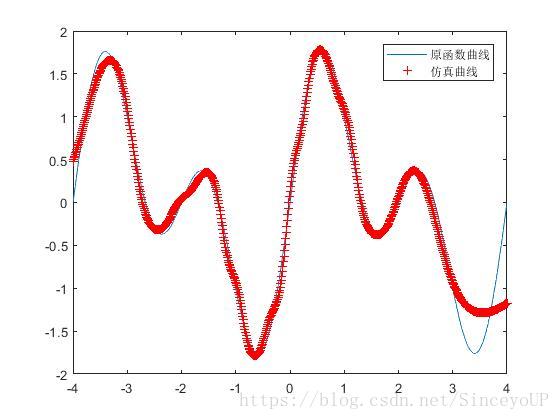
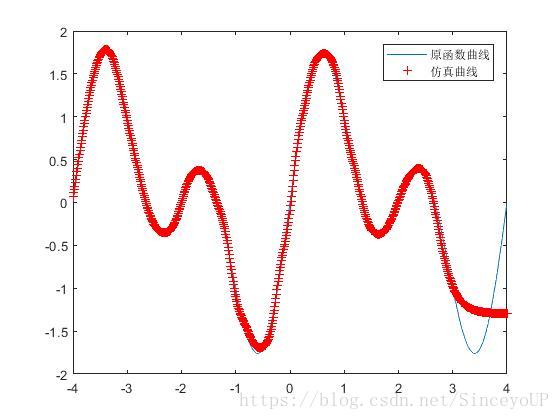
plot(x,t);
hold on
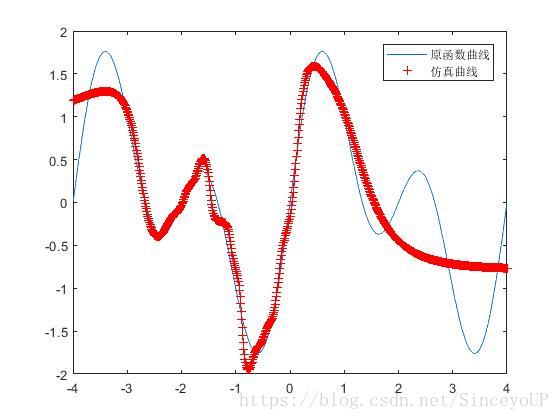
plot(x,y2,'r+');
legend('原函数曲线','仿真曲线')

(1)trainlm算法

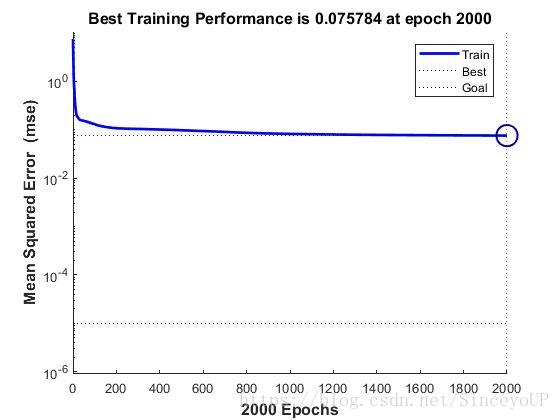
(2)traingdm算法

(3)trainrp算法

(4)traingdx算法

(5)traincgf算法