二分图匹配详解

二分图匹配

1.二分图的原始模型及相关概念

二分图又称作二部图，是图论中的一种特殊模型。
设 G=(V,E) 是一个无向图。如顶点集 V 可分割为两个互不相交的子集，并且图中每
条边依附的两个顶点都分属两个不同的子集。则称图 G 为二分图。我们将上边顶点集合称
为 X 集合，下边顶点结合称为 Y 集合，如下图，就是一个二分图。

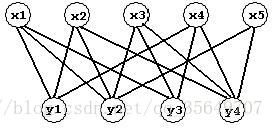
二分图的匹配：

给定一个二分图 G ，在 G 的一个子图 M 中， M 的边集 E 中的任意两条边都不依附于
同一个顶点，则称 M 是一个匹配。

最大匹配：

在二分图 G 中所有的匹配 M 中，边数最多的匹配，称为二分图的最大匹配。

完全匹配：

如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也
称作完备匹配。显然，完备匹配必然是一个最大匹配。
由完备匹配的定义可知：一个二分图有完备匹配，那么这个二分图的顶点个数必然为偶
数，且它的两个顶点集合的个数相等。

最佳匹配：

如果二分图 G 的每条边带权的话，权和最大的匹配叫做最佳匹配。

最佳完备匹配：

在加权二分图的所有完备匹配中，边权和最大的称为最佳完备匹配。

一般图最大匹配：

对于无向图 G=(V,E) ，图中满足两两不含公共端点的边集合 M⊂E 称为这张图的一
个匹配，集合大小 |M| 最大的匹配称为最大匹配。

2.求解二分图最大匹配

网络流算法

使用网络流算法：
实际上，可以将二分图最大匹配问题看成是最大流问题的一种特殊情况。
用网络流算法思想解决最大匹配问题的思路：
首先：建立源点 s 和汇点 t ，从 s 向 X 集合的所有顶点引一条边，容量为 1 ，从 Y 集合
的所有顶点向 T 引一条边，容量为 1 。
然后：将二分图的所有边看成是从 Xi 到 Yj 的一条有向边，容量为1。
求最大匹配就是求 s 到 t 的最大流。
最大流图中从 Xi 到 Yj 有流量的边就是匹配集合中的一条边。

匈牙利算法

发现了一篇写得非常好的博客，可以看看这里的解释：趣写算法系列之–匈牙利算法

3.常见模型

上面已经提到了图的匹配的概念，此外还有几个相关的有用的概念，在此我们再介绍除
匹配之外的三个概念：
记图 G=(V,E) 。

匹配：在 G 中两两没有公共端点的边集合 M⊂E 。
边覆盖： G 中的任意顶点都至少是 F 中某条边的端点的边集 F⊂E 。
独立集：在 G 中两两互不相连的顶点集合 S⊂V 。
顶点覆盖： G 中的任意边都有至少一个端点属于 S 的顶点集合 S⊂V 。

相应的也有：最大匹配，最小边覆盖，最大独立集，最小顶点覆盖。
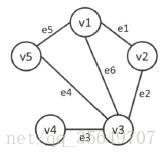
例如下图中，最大匹配为 {e1,e3} ，最小边覆盖为 {e1,e3,e4} ，最大独立集为 {v2,v4,v5} ，

三个重要等式：

在二分图中满足：
(1) 对于不存在孤立点的图， 最大匹配 + 最小边覆盖 = V
证明:通过最大匹配加边得到最小边覆盖。

(2) 最大独立集 +最小顶点覆盖= V
证明:独立集中若存在边，那么顶点覆盖不能覆盖完所有边，矛盾。

(3)|最大匹配| = |最小顶点覆盖|。
具体证明参考：
百度百科:Konig定理
二分图的最小顶点覆盖 最大独立集 最大团

有向图中应用二分匹配

求有向图最小路径覆盖：
对于有向图的最小路径覆盖，先拆点，将每个点分为两个点，左边是1-n个点，右边是1-n个点
然后每一条有向边对应左边的点指向右边的点。对此图求最大匹配，再用n-最大匹配即可。

证明：
将图中顶点看做n条边，每次加入一条有向边相当于合并两条边，又因为一个点只能经过一次，与匹配的性质一样。

例题

poj3041(求最小点覆盖)

有一张方格图，有些方格上有障碍，每次可消除某一行或某一列的障碍，求至少消灭几次。

解：每个有障碍格子的X向Y连边，那么这条边可以看做是一个障碍，一个顶点可以看做消除某一行或某一列，根据题意成功转化为最小点覆盖，套版即可。

#include
#include
#include
#include
#include
#include
#include
using namespace std;
const int Maxn=1e3+50;
const int Maxm=2e4+50;

inline int read()
{
    char ch=getchar();int i=0,f=1;
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch)){i=(i<<1)+(i<<3)+ch-'0';ch=getchar();}
    return i*f; 
}

int n,m,ans,before[Maxm],to[Maxm],last[Maxn],vis[Maxn],mate[Maxn],vt,ecnt=1;

inline void add(int x,int y)
{
    before[++ecnt]=last[x];
    last[x]=ecnt;
    to[ecnt]=y;
}

inline bool Hungary(int i)
{
    for(int e=last[i];e;e=before[e])
    {
        int v=to[e];
        if(vis[v]==vt)continue;
        vis[v]=vt;
        if(!mate[v]||Hungry(mate[v]))return mate[i]=v,mate[v]=i,true;
    }
    return false;
}

int main()
{
    n=read(),m=read();
    for(int i=1;i<=m;i++)
    {
        int x=read(),y=read()+n;
        add(x,y);add(y,x);
    }
    for(int i=1;i<=n;i++)
    {
        if(mate[i])continue;
        vt++;if(Hungary(i))++ans;
    }
    cout<

poj1422(有向图最小路径覆盖)

套版即可。

#include
#include
using namespace std;
const int Maxn=2e2+50,Maxm=2e4+50;

inline int read()
{
    char ch=getchar();int i=0,f=1;
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch)){i=(i<<1)+(i<<3)+ch-'0';ch=getchar();}
    return i*f; 
}

int T,n,m,vt,ans,mate[Maxn],to[Maxm],before[Maxm],last[Maxn],vis[Maxn],ecnt=1;

inline void add(int x,int y)
{
    before[++ecnt]=last[x];
    last[x]=ecnt;
    to[ecnt]=y;
}

inline bool Hungary(int i)
{
    for(int e=last[i];e;e=before[e])
    {
        int v=to[e];
        if(vis[v]==vt)continue;
        vis[v]=vt;
        if(!mate[v]||Hungary(mate[v]))return mate[i]=v,mate[v]=i,true;
    }
    return false;
}

int main()
{
    T=read();
    while(T--)
    {
        memset(last,0,sizeof(last));
        memset(mate,0,sizeof(mate));
        ecnt=1;ans=0;
        n=read(),m=read();
        for(int i=1;i<=m;i++)
        {
            int x=read(),y=read()+n;
            add(x,y);add(y,x); 
        }
        for(int i=1;i<=n;i++)
        {
            if(mate[i])continue;
            vt++;
            if(Hungary(i))ans++;
        }
        cout<

poj1486Sorting Slides(判断唯一匹配)

桌上有n张幻灯片杂乱地叠在一起，给出每张幻灯片的边界和页码坐标，求在不翻动的情况下哪些页码可以确定。
解：将每对可以匹配的连边后跑最大匹配。依次将匹配边删除判断是否可以找到另一匹配即可。

#include
#include
#include
using namespace std;
const int Maxn=55;

inline int read()
{
    char ch=getchar();int i=0,f=1;
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch)){i=(i<<1)+(i<<3)+ch-'0';ch=getchar();}
    return i*f; 
} 

int n,T,x1[Maxn],x2[Maxn],y1[Maxn],y2[Maxn];
int before[Maxn*Maxn*2],to[Maxn*Maxn*2],last[Maxn*2],ecnt,mate[Maxn*2],vis[Maxn*2],vt,ban[Maxn*Maxn*2];

inline void add(int x,int y)
{
    before[++ecnt]=last[x];
    last[x]=ecnt;
    to[ecnt]=y;
}

inline bool Hungary(int i)
{
    for(int e=last[i];e;e=before[e])
    {
        if(ban[e]||vis[to[e]]==vt)continue;
        vis[to[e]]=vt;
        if(!mate[to[e]]||Hungary(to[mate[to[e]]]))return mate[i]=e,mate[to[e]]=e^1,true;
    }
    return false;
}

int main()
{
    while(n=read(),n)
    {
        T++;ecnt=1;vt=0;
        memset(last,0,sizeof(last));memset(mate,0,sizeof(mate));memset(vis,0,sizeof(vis));memset(ban,0,sizeof(ban));
        for(int i=1;i<=n;i++)x1[i]=read(),x2[i]=read(),y1[i]=read(),y2[i]=read();
        for(int i=1;i<=n;i++)
        {
            int x=read(),y=read();
            for(int j=1;j<=n;j++)
            {
                if(x>=x1[j]&&x<=x2[j]&&y>=y1[j]&&y<=y2[j])add(i+n,j),add(j,i+n);
            }
        }
        int cnt=0;
        for(int i=1;i<=n;i++)
        {
            if(mate[i]){continue;}
            vt++;Hungary(i);
        }
        printf("Heap %d\n",T);
        for(int i=1;i<=n;i++)
        {
            int t1=mate[i],t2=t1^1;
            ban[t1]=ban[t2]=1;
            mate[i]=mate[to[t1]]=0;
            ++vt;
            if(Hungary(i))cnt++;
            else
            {
                mate[i]=t1,mate[to[t1]]=t2;
                printf("(%c,%d) ",'A'+i-1,to[mate[i]]-n);
            }
            ban[t1]=ban[t2]=0;
        }
        if(cnt==n)printf("none");
        printf("\n\n"); 
    }
}

poj2724PurifyingMachine(求二分图最小边覆盖)

告诉你一个二进制数字集合。每次可以清除一个或者两个（清楚两个要求二进制只有一位不同），求最小清除次数。

好题。
首先可以看出是一个无向图的最小路覆盖，还有一个重要的性质是边只会从奇数连向偶数。那么这就是一张二分图，由上面给出的公式可得最小路覆盖=点-最大匹配。套版即可。
（bitset是真的好用）

#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
const int Maxn=1e5+50;

inline int read()
{
    char ch=getchar();int i=0,f=1;
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch)){i=(i<<1)+(i<<3)+ch-'0';ch=getchar();}
    return i*f;
}

int n,m,tot,vt,ins[Maxn],mate[Maxn*2],vis[Maxn],last[Maxn*2],to[Maxn*4],before[Maxn*4],ecnt=1,que[Maxn],id[Maxn],cnt[2];
char ch[20];

inline void add(int x,int y)
{
    before[++ecnt]=last[x];
    last[x]=ecnt;
    to[ecnt]=y;
}

inline void insert()
{
    int t=0; 
    for(int i=1;i<=n;i++)if(ch[i]=='1')t+=(1<<(n-i));
    if(!ins[t])que[++tot]=t,ins[t]=1;
    for(int i=1;i<=n;i++)if(ch[i]=='*')t+=(1<<(n-i));
    if(!ins[t])que[++tot]=t,ins[t]=1;
}

inline bool Hungary(int i)
{
    for(int e=last[i];e;e=before[e])
    {
        int v=to[e];
        if(vis[v]==vt)continue;
        vis[v]=vt;
        if(!mate[v]||Hungary(mate[v]))return mate[i]=v,mate[v]=i,true;
    }
    return false;
}

int main()
{
    while(n=read(),m=read(),n,m)
    {
        memset(vis,0,sizeof(vis));memset(que,0,sizeof(que));memset(cnt,0,sizeof(cnt));
        memset(ins,0,sizeof(ins));memset(mate,0,sizeof(mate));memset(last,0,sizeof(last));
        memset(id,0,sizeof(id));ecnt=1;vt=0;tot=0;
        for(int i=1;i<=m;i++){scanf("%s",ch+1);insert();}
        for(int i=1;i<=tot;i++)
        {
            bitset<32> t=que[i];
            int bz=(t.count()&1);
            id[que[i]]=++cnt[bz]+(bz==1?(1<<(n-1)):0);
        }
        for(int i=1;i<=tot;i++)
        {
            for(int j=i+1;j<=tot;j++)
            {
                bitset<32>t=que[i]^que[j];
                if(t.count()==1)
                {
                    add(id[que[i]],id[que[j]]);
                    add(id[que[j]],id[que[i]]);
                }
            }
        }
        int ans=0;
        for(int i=1;i<=cnt[0];i++)
        {
            if(mate[i])continue;
            ++vt;
            if(Hungary(i))++ans;
        }
        cout<0]+cnt[1]-ans<