遗传算法解flowshop问题
遗传算法解决flowshop问题
1.遗传算法简介
参考:https://blog.csdn.net/u010451580/article/details/51178225
百度百科:遗传算法
总结遗传算法过程:选择 -> 交叉 -> 变异 -> 更新 -> 终止
2.flowshop问题简介
已知:有n 个工件需要在m台机器上流水加工。
工件上的约束:所有工件均在0时刻释放且在各机器上的加工顺序相同,每个工件在每台机器上只加工一次。
机器上的约束:每个机器某一个时刻最多只能加工一个工件,而且执行过程是非抢占的。
目标:给出调度方案,使调度总完工时间最小。
要求:算法复杂度在多项式时间内。
总结来说就是:n个工件在m台机器上流水加工,所有工件0时刻释放,且在机器上加工顺序相同,只加工一次。机器每时刻最多只能加工一个工件,同时,执行过程是非抢占的。那么转化为组合优化问题就是,需要给出m个1-n的排列,使得每台机器按相应的一个排列对工件进行加工,从而使得总加工时间最短。那么就需要找到这样的m个1-n的排列作为一个解,使总加工时间最短。当给出一个解时,通过动态规划可以很容易计算得到加工时间。
输入如下:
11 5
0 375 1 12 2 142 3 245 4 412
0 632 1 452 2 758 3 278 4 398
0 12 1 876 2 124 3 534 4 765
0 460 1 542 2 523 3 120 4 499
0 528 1 101 2 789 3 124 4 999
0 796 1 245 2 632 3 375 4 123
0 532 1 230 2 543 3 896 4 452
0 14 1 124 2 214 3 543 4 785
0 257 1 527 2 753 3 210 4 463
0 896 1 896 2 214 3 258 4 259
0 532 1 302 2 501 3 765 4 988optimum result:7038
说明:第一行是工件数和机器数,2-12行是每个工件在每台标号的机器上的加工时长如第二行就是第一个工件在0机器加工375,1机器加工12…
3.遗传算法代码
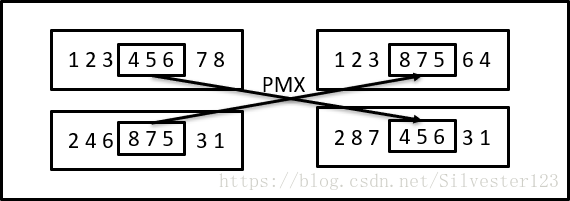
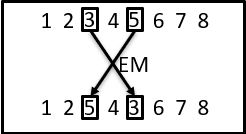
对于遗传算法,其关键点在初始化,交叉算子,变异算子、选择算子以及适应度的选择与确定。对于适应度的选择,本文以每个解的总时间花费作为一个个体的适应度;针对初始化,生成一个具有一定规模大小的种群,每个个体有m个染色体,每条染色体有n个基因,即一个染色体上有一个随机的排列;选择算子目前包括精英选择和轮盘赌方式,本文选择轮盘赌方式;对于交叉算子和变异算子,现有的交叉算子有AP,CX,ER,OX1,OX2,PMX,POS,VRR共八种,变异算子有DM,EM,ISM,IVM,SIM,SM共六种,本文选择PMX交叉算子和EM变异算子,二者操作方式如图;最后就是迭代种群,本文采取的方式是,将父代种群与子代种群合并,然后选取适应度小的一些个体作为下一代种群个体,同时保证种群大小不变。
具体遗传算子总结参考:https://blog.csdn.net/u012750702/article/details/54563515
PMX和EM操作如下:
/**
* date: 2018-06-14
* author: silvester
* (utf-8) 编译环境:gcc version 5.3.0 (GCC) -std=c++11
*/
#includefor(int j=0;j"%d %d",&k,&t);
infor[i][k]=t;
}
}
}
void swap(int *x,int *y)//交换两个元素
{
int temp=*x;
*x=*y;
*y=temp;
}
void randArray(int *a)//获取一个随机序列
{
for(int i=0;i//先初始化该序列
a[i]=i;
}
for(int i=0;i//然后随机交换两个位置n次
int rd=rand()%(n-i)+i;
swap(&a[i],&a[rd]);
}
}
int max(int a,int b){//取大
return a>=b?a:b;
}
/******GA*******/
#define GROUPSCALE 50//种群大小,即规模
#define SONNUM 50//孩子种群最大规模
int inheritance=50000;//迭代代数
double mutation=0.1;//变异概率
double crossover=0.8;//交叉概率,即生产儿子概率
struct Unit{//一个个体定义
int chromosome[MACHINE][JOB];//个体染色体MACHINE条,每条染色体JOB个基因
int fitness;//个体适应度
double proba;//根据适应度计算得到个体在种群中被选择做父本的概率
};
struct Unit group[GROUPSCALE];//定义种群
struct Unit sonGroup[SONNUM];//定义儿子种群
int newbornNum;//新生儿子个数
int indexcross_i;//即将交叉染色体片段起始位置
int indexcross_j;//即将交叉染色体片段终止位置
void printfUnit(Unit u){//输出某一个个体信息
for(int i=0;i//输出基因型
for(int j=0;j"%d%c",u.chromosome[i][j],j==n-1?'\n':' ');
}
}
//输出适应度
printf("%d\n",u.fitness);
printf("----------------\n");
}
int calculateTime_GA(Unit unit)//适应度函数,flowshop问题中,即为加工这些工件的时间花费
{
int time=0,fin_time[JOB];
memset(fin_time,0,sizeof(fin_time));
//对于m个排列,每台机器按照一个相应的排列顺序来加工工件,若工件还未到达,则等待
//动态规划计算一个解决方案的花费时间
for(int i=0;ifor(int j=0;jif(i==m-1) return time;
else time=0;
}
return 0;
}
void calculateProbality(int total)//计算种群各个个体被选择作为父本概率,传入的数为种群fitness之和
{
double tempTotalP=0.0;
// 由于是fitness越小,被选择概率越大,因此,需要做相应函数变化,而不能直接按比例得到
for(int i=0;igroup[i].proba=(1.0/(double)group[i].fitness)*(double)total;
tempTotalP+=group[i].proba;
}
for(int i=0;igroup[i].proba=group[i].proba/tempTotalP;
}
}
void init_GA()//初始化种群
{
int total=0;
for(int i=0;ifor(int j=0;jgroup[i].chromosome[j]);//每条染色体随机初始化一个排列
}
group[i].fitness=calculateTime_GA(group[i]);//计算这个个体fitness
total+=group[i].fitness;//累计种群fitness之和
}
calculateProbality(total);//计算种群个体被选择做父本概率
}
//挑选父本方式1:精英选择,直接选择种群中适应度最小的两个个体
void selectTwo(int &father_pos,int &mother_pos)
{
int one=0,minCost=INF;
for(int i=0;i//挑选第一个
if(minCost>group[i].fitness){
minCost=group[i].fitness;
one=i;
}
}
father_pos=one;
minCost=INF;
one=0;
for(int i=0;i//挑选第二个
if(i==father_pos) continue;
if(minCost>group[i].fitness){
minCost=group[i].fitness;
one=i;
}
}
mother_pos=one;
}
//挑选父本方式2:轮盘赌选择,模拟自然选择,依据被选择概率随机选择两个个体做父本
int selectOne(int conf)
{
double selectP=((double)(rand()%999)/998.0);
double sumP=0.0;
for(int i=0;igroup[i].proba;
if(selectPif(i==conf) return i+1;//解决选取的两个父本是同一个的问题
else return i;
}
}
return 0;
}
void getConflict(int Detection[],int Model[],int len_cross,int &len_conflict,int *conflict)
{
len_conflict=0;
for(int i=0;i//如果对Detection中的某个基因在Model中也存在,则不存在冲突否则存在冲突
{
int flag=1;
for(int j=0;jif(Detection[i]==Model[j]){
j=len_cross;
flag=0;
}
}
if(flag){
conflict[len_conflict]=Detection[i];//将冲突基因存在conflict中
len_conflict++;
}
}
}
void handleConflict(Unit conflictUnit,int *Detection_Conflict,int *Model_Conflict,int len_conflict,int k,int *p)
{
// 解决冲突,使得一个排列中不出现重复的编号
for(int i=0;i//共len_conflict个冲突编号
int flag=0;
int index=0;
//重复的编号在Model_Conflict中
//以下对非交换区域找出编号重复的位置
for(index=0;indexindex++){
if(Model_Conflict[i]==conflictUnit.chromosome[k][index])
{
flag=1;
break;
}
}
if(!flag){
for(index=indexcross_j+1;indexindex++){
if(Model_Conflict[i]==conflictUnit.chromosome[k][index])
break;
}
}
//将重复的编号替换,替换编号在Detection_Conflict中
conflictUnit.chromosome[k][index]=Detection_Conflict[i];
}
for(int i=0;i//终止将这条新染色体赋值,传给孩子
p[i]=conflictUnit.chromosome[k][i];
}
}
void Crossover_PMX(Unit fa,Unit mo)//采用PMX方式进行交叉变异
{
Unit son_one;//孩子1
Unit son_two;//孩子2
son_one.fitness=0;
son_two.fitness=0;
for(int k=0;k//对m条染色体交叉
indexcross_i=rand()%n;
indexcross_j=rand()%n;//确定交叉片段起始和终止位置
if(indexcross_i>indexcross_j){
int temp=indexcross_i;
indexcross_i=indexcross_j;
indexcross_j=temp;
}
int father_cross[JOB];//记录父亲交叉片段
int mother_cross[JOB];//记录母亲交叉片段
int len_cross=0;
for(int i=indexcross_i;i<=indexcross_j;i++){
father_cross[len_cross]=fa.chromosome[k][i];
mother_cross[len_cross]=mo.chromosome[k][i];
len_cross++;
}
int conflict_fa[JOB];//记录父亲产生的冲突片段
int conflict_ma[JOB];//记录母亲产生的冲突片段
int len_conflict=0;//冲突基因个数
getConflict(father_cross,mother_cross,len_cross,len_conflict,conflict_fa);//获取父亲冲突基因片段
getConflict(mother_cross,father_cross,len_cross,len_conflict,conflict_ma);//获取母亲冲突基因片段
for(int i=indexcross_i;i<=indexcross_j;i++){//将父亲和母亲交叉片段进行交换
int temp_node=fa.chromosome[k][i];
fa.chromosome[k][i]=mo.chromosome[k][i];
mo.chromosome[k][i]=temp_node;
}
//分别对父亲和母亲处理冲突的基因片段,这样可以得到两个孩子
handleConflict(fa,conflict_fa,conflict_ma,len_conflict,k,son_one.chromosome[k]);
handleConflict(mo,conflict_ma,conflict_fa,len_conflict,k,son_two.chromosome[k]);
}
sonGroup[newbornNum++]=son_one;//将两个孩子加入子代种群
sonGroup[newbornNum++]=son_two;
}
void Mutation(int index,int k)//对第index个个体的第k条染色体进行变异
{
int gen_i=rand()%n;
int gen_j=rand()%n;
//变异采取的方式是随机交换两个基因
int temp=sonGroup[index].chromosome[k][gen_i];
sonGroup[index].chromosome[k][gen_i]=sonGroup[index].chromosome[k][gen_j];
sonGroup[index].chromosome[k][gen_j]=temp;
}
int UpdateGroup()//种群更新
{
Unit tempP;
//对新生种群按适应度从小到大排序
for(int i=0;ifor(int j=newbornNum-1;j>i;j--){
if(sonGroup[i].fitness>sonGroup[j].fitness){
tempP=sonGroup[i];
sonGroup[i]=sonGroup[j];
sonGroup[j]=tempP;
}
}
}
//对原始种群按适应度从小到大排序
for(int i=0;ifor(int j=GROUPSCALE-1;j>i;j--){
if(group[i].fitness>group[j].fitness){
tempP=group[i];
group[i]=group[j];
group[j]=tempP;
}
}
}
//将新生种群中fitness较小的个体替换至原始种群,从而得到新种群
int j=GROUPSCALE-1;
for(int i=0;iif(sonGroup[i].fitness<group[j].fitness){
group[j]=sonGroup[i];
j--;
}
else break;
}
int total=0;
for(int i=0;i//计算新种群所以个体适应度之和
total+=group[i].fitness;
}
return total;
}
void GA()
{
init_GA();
int iter=0;
int minFitness=INF,minGeneration;
Unit minUnit;
while(iterint M=GROUPSCALE-GROUPSCALE/2;//每次交叉产生两个儿子,故只需M次交叉
newbornNum=0;//记录新生儿个数
while(M){
//1.选择,两种选择方式
//(1)轮盘赌选择
int pos1=selectOne(-1);
int pos2=selectOne(pos1);
//(2)精英选择
//int pos1,pos2;
//selectTwo(pos1,pos2);
//确定两个父本个体
Unit father=group[pos1];
Unit mother=group[pos2];
//2.交叉
// int M=GROUPSCALE-GROUPSCALE/2;//每次交叉产生两个儿子,故只需M次交叉
// newbornNum=0;//记录新生儿个数
// while(M){
double Is_crossover=((double)(rand()%999)/998.0);
if(Is_crossover<=crossover){//依概率判断是否交叉
//采用PMX遗传算子交叉
Crossover_PMX(father,mother);
}
M--;
}
//3.变异
for(int i=0;i//对每个新生儿,每条染色体依概率判断是否发生变异
for(int k=0;kdouble rateVaration=double(rand()%999/998.0);
if(rateVaration//计算新生儿适应度
}
//4.更新
int totaltime=UpdateGroup();//更新种群并得到新种群个体适应度之和
calculateProbality(totaltime);//计算新种群个体被选择概率
iter++;//代数自加
int minCost=INF,pos;//求出此代最优
for(int i=0;iif(minCost>group[i].fitness){
minCost=group[i].fitness;
pos=i;
}
}
//记录历代最优
if(minFitness>minCost){//更新整体历代最优
minFitness=minCost;
minUnit=group[pos];
minGeneration=iter;
}
}
//5.输出最优
printf("Best, No.%d generation:\n",minGeneration);//最优出现代数
printfUnit(minUnit);//最优解
}
int main()
{
inputInformation();//输入
long start_time=clock();
srand((unsigned)(time(NULL)));//随机种子
/*****GA*****/
printf("---------GA----------\n");
GA();
long end_time=clock();//输出算法运行时间
printf("time = %ld ms\n",end_time-start_time);
return 0;
} 输出结果:
五个测试用例如下:
11 5
0 375 1 12 2 142 3 245 4 412
0 632 1 452 2 758 3 278 4 398
0 12 1 876 2 124 3 534 4 765
0 460 1 542 2 523 3 120 4 499
0 528 1 101 2 789 3 124 4 999
0 796 1 245 2 632 3 375 4 123
0 532 1 230 2 543 3 896 4 452
0 14 1 124 2 214 3 543 4 785
0 257 1 527 2 753 3 210 4 463
0 896 1 896 2 214 3 258 4 259
0 532 1 302 2 501 3 765 4 988
13 4
0 654 1 147 2 345 3 447
0 321 1 520 2 789 3 702
0 12 1 147 2 630 3 255
0 345 1 586 2 214 3 866
0 678 1 532 2 275 3 332
0 963 1 145 2 302 3 225
0 25 1 24 2 142 3 589
0 874 1 517 2 24 3 996
0 114 1 896 2 520 3 541
0 785 1 543 2 336 3 234
0 203 1 210 2 699 3 784
0 696 1 784 2 855 3 512
0 302 1 512 2 221 3 345
12 5
0 456 1 537 2 123 3 214 4 234
0 789 1 854 2 225 3 528 4 123
0 876 1 632 2 588 3 896 4 456
0 543 1 145 2 669 3 325 4 789
0 210 1 785 2 966 3 147 4 876
0 123 1 214 2 332 3 856 4 543
0 456 1 752 2 144 3 321 4 210
0 789 1 143 2 755 3 427 4 123
0 876 1 698 2 322 3 546 4 456
0 543 1 532 2 100 3 321 4 789
0 210 1 145 2 114 3 401 4 876
0 124 1 247 2 753 3 214 4 543
14 4
0 456 1 856 2 963 3 696
0 789 1 930 2 21 3 320
0 630 1 214 2 475 3 142
0 214 1 257 2 320 3 753
0 573 1 896 2 124 3 214
0 218 1 532 2 752 3 528
0 653 1 142 2 147 3 653
0 214 1 547 2 532 3 214
0 204 1 865 2 145 3 527
0 785 1 321 2 763 3 536
0 696 1 124 2 214 3 214
0 532 1 12 2 257 3 528
0 12 1 345 2 854 3 888
0 457 1 678 2 123 3 999
10 6
0 333 1 991 2 996 3 123 4 145 5 234
0 333 1 111 2 663 3 456 4 785 5 532
0 252 1 222 2 222 3 789 4 214 5 586
0 222 1 204 2 114 3 876 4 752 5 532
0 255 1 477 2 123 3 543 4 143 5 142
0 555 1 566 2 456 3 210 4 698 5 573
0 558 1 899 2 789 3 124 4 532 5 12
0 888 1 965 2 876 3 537 4 145 5 14
0 889 1 588 2 543 3 854 4 247 5 527
0 999 1 889 2 210 3 632 4 451 5 856注:以上所有操作均在作者在网上搜集资料后,在个人电脑上实验成功,若读者实验时失败,可能由一些未知因素导致,可与作者联系。编写的教程可能由于疏忽出错,请与作者联系。