扩展中国剩余定理 EXCRT

扩展中国剩余定理 EXCRT

题目描述

给定$n$个同余式，$m_1,m_2...,m_n$不一定互质

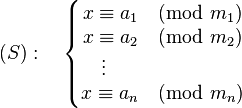
问，满足上述同余式最小的$x$是多少

解决方法

显然不能再用CRT的方法来求解了
那么我们考虑逐一进行求解
假设当前已经求出前$k-1$个方程组的解，记为$x$
且有$M={\prod }_{i=1}^{k-1}{m}_i$
那么前k-1个方程组的同解即为$x+i\ast M,i\in Z$

那么对于当前加入的第$k$个方程组，我们其实就是需要找到一个$t$，使得$x+t\ast M\equiv a_k(\mathrm{m}\mathrm{o}\mathrm{d}{m}_k)$
稍微转化一下这个式子$\Rightarrow t\ast M\equiv a_k-x(\mathrm{m}\mathrm{o}\mathrm{d}{m}_k)$
那么就可以用拓欧来解决这个式子了，如果该方程无解，那么整个方程组无解，否则继续解下去

可以发现EXCRT的本质就是求解n次拓展欧几里得

例题 P4777-板子

代码

#include
#define int long long
using namespace std;
int read(){
     
	int f=1,re=0;char ch;
	for(ch=getchar();!isdigit(ch)&&ch!='-';ch=getchar());
	if(ch=='-'){
     f=-1,ch=getchar();}
	for(;isdigit(ch);ch=getchar()) re=(re<<3)+(re<<1)+ch-'0';
	return re*f; 
}
int k,a[100009],b[100009];
int ksm(int a,int b,int mod){
     
	int ans=1;
	while(b){
     
		if(b&1) ans=ans*a%mod;
		a=a*a%mod;
		b>>=1;
	}return ans;
}
int qmul(int a,int b,int mod){
     
	int ans=0;
	while(b){
     
		if(b&1) ans=(ans+a)%mod;
		a=(a+a)%mod;
		b>>=1;
	}return ans;
}
int exgcd(int a,int b,int &x,int &y){
     
	if(b==0){
     x=1,y=0;return a;}
	int d=exgcd(b,a%b,x,y);
	int tmp=x;
	x=y,y=tmp-a/b*y;
	return d;
}
int excrt(){
     
	int ans=b[1],lcm=a[1],x,y;
	for(int i=2;i<=k;i++){
     
		int c=(b[i]-ans%a[i]+a[i])%a[i];
		int d=exgcd(lcm,a[i],x,y);
		if(c%d) return -1;
		int r=a[i]/d;
		x=qmul(x,c/d,r);
		ans+=x*lcm;
		lcm*=r;
		ans=(ans%lcm+lcm)%lcm;
	}return ans=(ans%lcm+lcm)%lcm;
}
signed main(){
     
	k=read();
	for(int i=1;i<=k;i++) a[i]=read(),b[i]=read();
	printf("%lld\n",excrt());
	return 0;
}