素数的判定
目录
- 【概述】
- 【试除法】
- 【孪生素数法】
- 【例题】
- AcWing 866. 试除法判定质数(模板)
- HDU 2012 素数判定
【概述】
素数,又称质数,是指一个大于 1 1 1 的正整数,如果除了 1 1 1 和它本身以外,没有其他的约数,例如 2 、 3 、 5 、 73021377 2、3、5、73021377 2、3、5、73021377 等;反之就是合数。
1 1 1 既不是素数也不是合数。
素数定理: π ( x ) ∼ x l n x \pi (x)\sim \frac{x}{lnx} π(x)∼lnxx,其中 π ( x ) π(x) π(x) 表示不超过 x x x 的素数的个数
质数分布密度定理:素数的分布越来越稀疏,当 1e18 内的任意两个素数的差不会很大(不会超过 300)
【试除法】
从素数的定义可知,只有 2 , 3 , … , n − 1 2, 3,…, n-1 2,3,…,n−1 都不能整除 n n n, n n n 才能判定为素数,而只要有一个能整除 n n n , n n n 就可以判定为非素数。时间复杂度为 O ( n ) O(n) O(n)。
bool isPrime(int n)
{
if(n < 2) return false;
for(int i = 2; i < n; i++)
if(n % i == 0)
return false;
return true;
}
优化:注意到如果在 2 ∼ n − 1 2 \sim n-1 2∼n−1 中存在 n n n 的约数,不妨设为 k k k,即 n % k = = 0 n \% k ==0 n%k==0,那么由 k ∗ ( n / k ) = = n k*(n/k) ==n k∗(n/k)==n 可知, n / k n/k n/k 也是 n n n 的一个约数,且 k k k 与 n / k n/k n/k 一定满足其中一个小于 s q r t ( n ) sqrt(n) sqrt(n)、另一个大于 s q r t ( n ) sqrt(n) sqrt(n)。
这启发我们,只需要判定 n n n 能否被 2 , 3 , … , ⌊ s q r t ( n ) ⌋ 2, 3 ,…, \lfloor sqrt(n) \rfloor 2,3,…,⌊sqrt(n)⌋ 整除即可,该算法的复杂度为 O ( s q r t ( n ) ) O(sqrt(n)) O(sqrt(n))。(其中 ⌊ x ⌋ \lfloor x \rfloor ⌊x⌋ 表示对 x x x 向下取整)
// 判断某个数是否是素数
int isPrime(int n)
{
if(n < 2) return 0;
int sqr = (int)sqrt(1.0 * n);
for(int i = 2; i <= sqr; i++) // 遍历2~根号n
if(n % i == 0)
return 0;
return 1;
}
如果 n n n 没有接近 i n t int int 型变量的范围上界,那么可以有更简单的写法,如下。
这样写会当 n n n 接近 i n t int int 型变量的范围上界时导致 i ∗ i i*i i∗i 溢出 (当然 n n n 在 1 0 5 10^5 105 以内都会是安全的),解决的办法是将 i i i 定义为 long long 型,这样就不会溢出了。
bool isPrime(int n)
{
if(n < 2) return false;
for(int i = 2; i * i <= n; i++)
if(n % i == 0)
return false;
return true;
}
综上,推荐写法:
bool is_prime(int x)
{
if (x < 2) return false;
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0)
return false;
return true;
}
【孪生素数法】
孪生素数:孪生素数指的是间隔为 2 2 2 的相邻素数。
1、当 n ≥ 6 n \geq 6 n≥6, n − 1 n - 1 n−1 和 n + 1 n + 1 n+1 为孪生素数,那么 n n n 一定是 6 6 6 的倍数。
推论:当 x ≥ 1 x \geq 1 x≥1, ( 6 x − 1 ) (6x - 1) (6x−1) 或 ( 6 x + 1 ) (6x + 1) (6x+1) 不是素数时,它们的质因子不包括 2 2 2 和 3 3 3 的倍数。
2、素数分布规律:当 n ≥ 5 n \geq 5 n≥5 时,如果 n n n 为素数,那么 n % 6 = 1 ∣ ∣ n % 6 = 5 n \% 6 = 1\ ||\ n \% 6 = 5 n%6=1 ∣∣ n%6=5,即 n n n 一定出现在 6 x ( x ≥ 1 ) 6x\ (x≥1) 6x (x≥1)两侧。
总结:就是说大于等于5的素数一定是分布在6倍数的左右两侧,但在6倍数左右两侧的数不一定是素数
// 判断某个数是否是素数
int IsPrime(int n)
{
if(n <= 1) return 0;
if(n == 2 || n == 3) return 1;
if(n % 6 != 1 && n % 6 != 5) return 0; // 不是6x两侧的数肯定不是素数
for(int i = 5; i <= (int)sqrt(n); i += 6) // 再对6x两侧的数进行判断
if(n % i == 0 || n % (i + 2) == 0)
return 0;
return 1;
}
【例题】
AcWing 866. 试除法判定质数(模板)
题目链接:点击这里
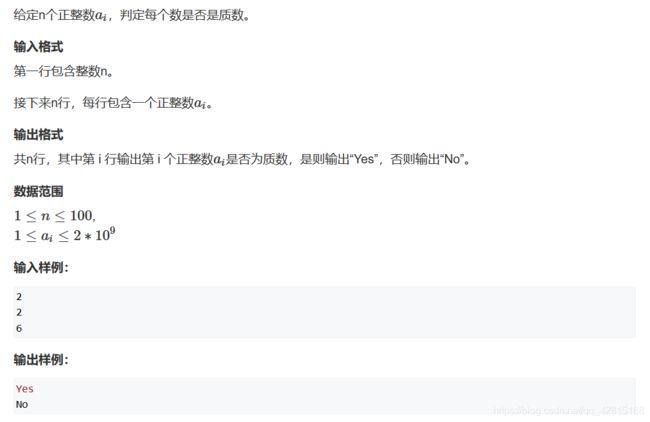
时间复杂度为 O ( n ) O(\sqrt{n}) O(n),AC:
#includeHDU 2012 素数判定
题目链接:点击这里
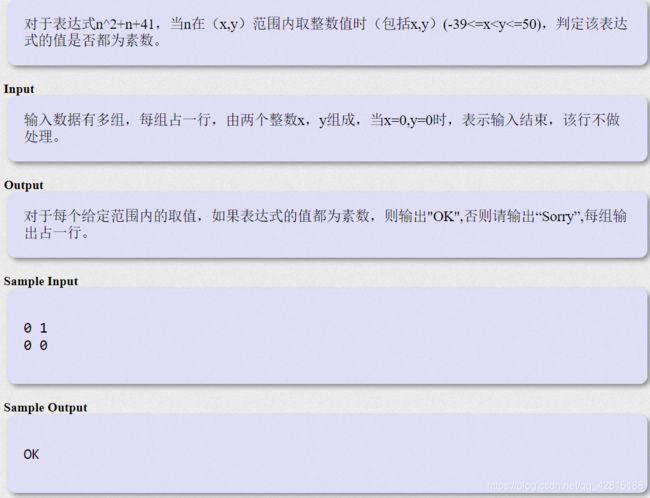
AC代码:
#include