数学建模笔记——评价类模型（二）

好的，今天继续研究评价类模型的相关算法。实不相瞒，虽然我才写到第二个算法，但是已经听了几十节课了，清风老师的课程确实蛮不错的，实用性比较强。相关的模型、算法基本上越往后越难，所以珍惜现在比较容易理解的评价类模型吧hhh。

在这里要说明一下，小白本白只是一个即将大三的本科生，目前比较容易理解的模型我还能写得完整一些。之后很多模型会涉及较为复杂的数学推导，我可能很难完整地从原理去描述了，只能着重于实际应用方面。请各位谅解啦。

ok，我们继续学习评价类模型算法。

（注：以下案例均来自我所听的网课）

回顾

上一篇文章我们介绍了一个简单又实用的评价打分方法——层次分析法。同时我们也提到了，层次分析法有一些缺陷之处。首先就是主观性较强，层次分析法往往是专家用来打分的方法，但建模比赛中没有专家，判断矩阵只能我们自己填；其次，当指标或者方案层数量较多时，我们两两比较得出的判断矩阵和一致矩阵可能会出现较大的差异（想一想你的心理预期，有多符合那个乘法关系），判断矩阵的填写也会比较麻烦（例如要问$C_{20}^2$次问题）；再者，层次分析法往往用于没有相关数据的问题，我们的打分也是按照判断矩阵给出的，如果已经有了数据，再主观打分就不太合适了。

看看这个题目

给出$A—T$二十条河流的水质指标及具体数据，请建立合适的模型，给这些河流的水质从高到低排排序。嗯，现在再用层次分析法，是不是就不太合适了……

TOPSIS算法

TOPSIS算法是解决上述问题的一个比较合适的算法，其全称是$TechniqueforOrderPreferencebySimilaritytoanIdealSolution$，通俗的翻译则是“优劣解距离法”。这个翻译可以说是指向了此算法的本质，我们接下来慢慢谈。

我们依然从一个简单的问题入手。小明同学考上南大之后，不知不觉就迎来了第一次高数考试，他及其舍友的分数如下。

现在我们要根据他们的成绩，给他们进行打分，要求分数可以合理地表达其成绩的高低。hhh可能会有人觉得这个问题比较奇怪，成绩本身就可以作为所谓的分数了，实在不行我们还有GPA，怎么还要打分？因为这只是一个例子，事实上在许多实际问题中，我们只有数据，例如上面水质问题的含氧量，PH值，并没有这样一个分数。再者，实际问题中有很多的指标，其量纲经常不同，但我们需要通过这些数据得出一个综合的分数。因此我们很有必要对数据进行一定的处理，同时找到一个综合打分的方法。

所以我们有一个很直接的想法，就是对分数进行归一化处理，例如清风的最后得分就是$\frac{99}{89+60+74+99}=0.307$。嗯，这个想法很合理。即一个人的成绩占总成绩的比重，就可以作为这个人在总体中的得分。但是注意了，这里只有一个指标，所以我们可以直接用这个得分作为排序标准。如果还有一些指标，同样进行类似的操作，实际上就相当于我们对数据进行了处理，消去了量纲的影响罢了。结果就是，一番操作过后，留给我们的仍然是一个得分表格，只不过里面是已经被处理过的数据，但还是没能给出排名。

这里提出一个小问题，我们把PH值作为衡量水质的一个标准，其范围是0~14，PH=7时最好，所以PH=7时相关指标得分应该最高。这时候就不能像成绩那样，直接求和算比重了吧，那应该怎么处理呢？

ok，我们继续。上述的操作只是对数据进行了处理，我们还是需要一个打分的标准。有同学就会想到，赋权，然后打分。这就回到了我们层次分析法的内容。还是那些问题，主观性比较强，指标太多时操作起来不准确且麻烦，对数据的利用不充分等等。

这里就可以引入TOPSIS的想法了。事实上我们的目的是对方案给出一个排序，只要数据有了，我们就可以根据这些数据，构造出一个所有方案组成的系统中的理想最优解和最劣解（我感觉最劣解和理想不搭，就直接用最劣解称呼吧）。而TOPSIS的想法就是，我们通过一定的计算，评价系统中任何一个方案距离理想最优解和最劣解的综合距离。如果一个方案距离理想最优解越近，距离最劣解越远，我们就有理由认为这个方案更好。那理想最优解和最劣解又是什么呢？很简单，理想最优解就是该理想最优方案的各指标值都取到系统中评价指标的最优值，最劣解就是该理想最劣方案的各指标值都取到系统中评价指标的最劣值。这么说可能不是很清楚，举个例子。

如果我们只有一个指标，例如上图中的成绩，那么理想最优解就是99分，注意，不是满分100分，理想最优解中的数据都是各方案中的数据，而不要选择方案中没有的数据。不然如果是GDP这种上不封顶的指标，理想最优取值岂不是正无穷了……同理，该系统中的最劣解是60。

那如果有两个指标呢？例如我们引入一个“与他人争吵的次数”，用来衡量情商，给出相应的数据表格。

按照我们的一般想法，与他人争吵的次数应该是越小越好，所以我们可以用向量表达这个系统中的理想最优解，也就是$[99,0]$，取清风的成绩和小王的争吵次数，最劣解就是$[60,3]$，取小王的成绩和清风的争吵次数。

现在我们知道了如何取得理想最优解和最劣解，那如何衡量某一个方案与理想最优解和最劣解的综合距离呢？TOPSIS用下面一个表达式进行衡量：$\frac{某一方案-最劣解}{理想最优解-最劣解}$。可以发现，如果方案取到了理想最优解，其表达式取值为1；如果方案取到了理想最劣解，其表达式取值为0。我们便可以用这个表达式来衡量系统中某一个方案距离理想最优解和最劣解的综合距离，也直接用它给方案进行打分。

相信到这里大家对于TOPSIS的基本思想已经差不多理解了，之后就是实际操作的问题了。我们都知道，“方案 - 最劣解”这种东西只是方便理解，确实也是我编出来的，实际中方案根本不能做差。所以我们只能用数据来求出这么一个距离。对于某一个指标的数据，我们可以用$\frac{x-min}{max-min}$来衡量综合距离。如果只有成绩这一个指标，其计算很简单，例如清风的得分就是$\frac{99-60}{99-60}=1$，其余人的成绩可以依次给出。对于“争吵次数”这个指标，清风的得分可以是$\frac{3-3}{0-3}=0$，虽然也能计算，但其分母是个负值，还是不太习惯。那如果对于PH值，7是最优解，0和14哪一个看成最劣解用于计算呢？亦或者如果某个指标处在10~20之间最佳，那最优解最劣解又如何衡量呢？这便是我们遇到的问题。除此之外，由于数据的量纲不同，在实际的计算过程中也会出现这样或者那样的问题，因此我们也有必要对于原数据进行相关的处理。

首先，我们解决第一个问题，有些指标的数据越大越好，有些则是越小越好，有些又是中间某个值或者某段区间最好。我们可以对其进行“正向化处理”，使指标都可以像考试分数那样，越大越好。

我们可以把指标分为四类，如下表所示。

所谓的正向化处理，就是将上述的四种指标数据进行处理，将其全部转化为极大型指标数据，这样我们计算时问题就少一点，码代码时也更加统一。

对于极小型指标，例如费用，争吵次数，我们可以用${\hat{x}}_i=max-x_i$将其转化为极大型，如果所有元素都为正数，也可以使用${\hat{x}}_i=\frac{1}{x_i}$。示例如下。

对于中间型指标，如果其最佳数值是$x_{best}$，我们可以取$M=max\{|x_i-x_{best}|\}$，之后按照${\hat{x}}_i=1-\frac{x_i-x_{best}}{M}$转化，示例如下。

对于区间型指标，如果其最佳区间是$[a,b]$，我们取$M=max\{a-min\{x_i\},max\{x_i\}-b\}$，之后按照$${\hat{x}}_i=\{\begin{array}{ll}1-\frac{a-x_i}{M},& x_i<a\\ 1,& a<x_i<b\\ 1-\frac{x_i-b}{M},& x_i>b\end{array}$$转化，示例如下。

至此，我们已经将所有的数据都转化为极大型数据了，可以很好地使用$\frac{x-min}{max-min}$来进行打分。但是为了消除不同的数据指标量纲的影响，我们还有必要对已经正向化的矩阵进行标准化。在概率统计中，标准化的方法一般是$\frac{X-EX}{\sqrt{DX}}$，不过这里我们不采用。我们记标准化后的矩阵为$Z$，其中$z_{ij}=\frac{x_{ij}}{\sqrt{{\sum }_{i=1}^n{x_{ij}}^2}}$，也就是$\frac{每一个元素}{\sqrt{其所在列的元素的平方和}}$。

现在我们已经对数据进行了相应的处理，可以计算每一个方案的的得分了，也就是所谓的距离。由于我们一个方案具有多个指标，因此我们可以用向量$z_i$来表达第$i$个方案。假设有n个待评价的方案，m个指标，此时$z_i=[z_{i1},z_{i2},...,z_{im}]$。由这n个向量构成的矩阵也就是我们的标准化矩阵$Z$了。（实在是打不好这个样子……）

之后我们就可以从中取出理想最优解和最劣解了，经过了正向化处理和标准化处理的评分矩阵$Z$，里面的数据全部是极大型数据。因此我们取出每个指标，即每一列中最大的数，构成理想最优解向量，即$$\begin{gathered} z^{+}=[z_1^{+},z_2^{+},...,z_m^{+}]= \\ [max\{z_{11},z_{21},...,z_{n1}\},max\{z_{12},z_{22},...,z_{n2}\},...,max\{z_{1m},z_{2m},...,z_{nm}\}] \end{gathered}$$。
同理，取每一列中最小的数计算理想最劣解向量，$$\begin{gathered} z^{-}=[z_1^{-},z_2^{-},...,z_m^{-}]= \\ [min\{z_{11},z_{21},...,z_{n1}\},min\{z_{12},z_{22},...,z_{n2}\},...,min\{z_{1m},z_{2m},...,z_{nm}\}] \end{gathered}$$。

($z^{+}$就是$z_{max}$，$z^{-}$就是$z_{min}$)

现在我们可以计算得分了，之前我们的计算公式是$\frac {z_i-z_{min}}{z_{max}-z_{min}} \ $也就是$\ \frac {z_i-z_{min}}{(z_{max}-z_i)+(z_i-z_{min})}$，嗯，我们变形成了\cdot$\frac {z与z_{min}的距离}{z与z_{max}的距离\ +\ z与z_{min}的距离}$。为什么要这样变形呢？因为大家都是这么用的……好吧，其实我们接下来是使用欧几里得距离来衡量两个方案的距离，变形前后分母的计算结果其实是不同的。我个人认为这样变形更有利于说明问题，即我们衡量的得分是考虑到某个方案距离最优解和最劣解的一个综合距离。不然的话，所有方案计算得分时分母都是相同的，相当于只衡量了分子，也就是距离最劣解的距离。那应该还是采用综合衡量的方式会好一点儿吧，你觉得呢？

嗯，我就默认大家都同意这个说法了。我们继续计算得分，对于第$i$个方案$z_i$，我们计算它与最优解的距离$d_i^{+}=\sqrt{{\sum }_{j=1}^m(z_j^{+}-z_{ij}{)}^2}$，与最劣解的距离为$d_i^{-}=\sqrt{{\sum }_{j=1}^m(z_j^{-}-z_{ij}{)}^2}$。我们记此方案的得分为$S_i$，则$S_i=\frac{d_i^{-}}{d_i^{+}+d_i^{-}}$，也可以理解为我们上文一直在说的综合距离。很明显，$0\le S_i\le 1$，且$d_i^{+}$越小，也就是该方案与最优解的距离越小时，$S_i$越大；$d_i^{-}$越小，也就是该方案与最劣解的距离越小时，$S_i$越小。这种计算方式同时考虑了该方案与最优解和最劣解的距离。

这个时候我们就有了每个方案的分数了，按分数排排序，就知道哪个方案好一点儿哪个方案次一点儿了。还可以按照这个得分再进行一次归一化，不过我觉得没什么必要了。

嗯，基本部分讲完啦。

总结

总结一下。使用TOPSIS算法的一个先决条件就是要有数据，最好全部是定量数据，如果是定性数据或者定序数据，但能够分别优劣，也可以按照定量数据来处理。之后就开始操作:

1. 将原始数据矩阵正向化。
   也就是将那些极小性指标，中间型指标，区间型指标对应的数据全部化成极大型指标，方便统一计算和处理。
2. 将正向化后的矩阵标准化。
   也就是通过标准化，消除量纲的影响。
3. 计算得分并排序
   公式就是$S_i=\frac{d_i^{-}}{d_i^{+}+d_i^{-}}$。

这次好像还没有给一个完整的过程，嗯，我就把PPT里的完整过程放在这里供大家参考。
这是原始数据矩阵

我们对其进行正向化

我们再对其进行标准化

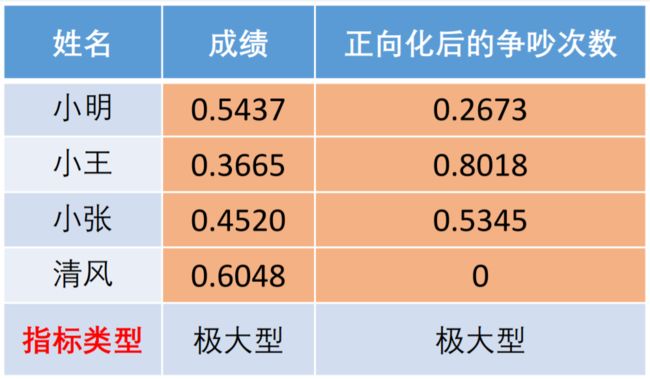
最后计算得分给出排名

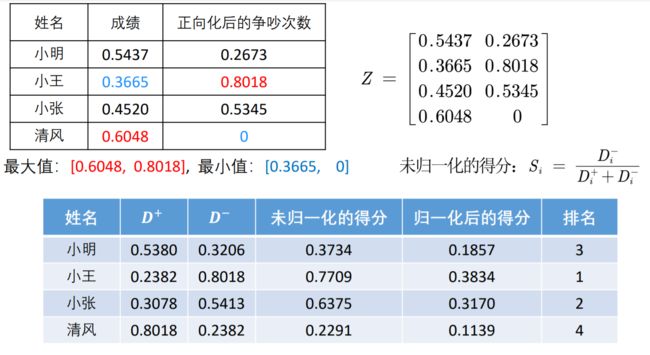
嗯，这个例子告诉我们，成绩很重要，但是情商更重要hhh。小王虽然只考了60分，但也及格了，而且他从不与人争吵，所以我们可以给他一个最好的评价hhh。

拓展

TOPSIS是不是又简单又使用呢？其实我们还可以进行一点点儿的拓展，不想打字了，看下图。

我们可以看到，在计算距离时，我们其实默认每个指标的权重是相同的，但实际问题中，不同的指标重要程度可能是不一样的。例如评奖学金的时候，成绩往往是最重要的，之后还有参与活动分，志愿服务分等等，他们的权重又低一点。因此，在实际的应用中，我们也可以给指标进行赋权，将权重放到计算距离的公式中。如图。

带上了权重之后，不同的指标发挥的影响就不一样了，带权重的评价也往往是实际生活中很常见的一种评价方式。

那在建模中如何确定权重呢？如果是日常生活向的评价，我们可以使用层次分析法，结合常识给出。如果是比较专业的评价指标，我们可以查询资料，看看别人怎么研究的。还有一种方法叫熵权法，也是这套课程的内容，不过限于篇幅，就留到之后再提吧。

局限性

TOPSIS法有什么局限性呢？其实也是有的，例如没有数据你就行不通了吧hhh。不过在实际建模中，倒也不必考虑太多的局限性，知道每个模型的适用条件就好了。到时候见招拆招，增删查改，尽力而为就好了。一个没有参加过比赛的小白说这些是不是有点儿不妥……不管了，反正就是碰到什么题用对应的模型，实在不行就试着综合综合，总能有个结果的hhh

嗯，就这样，拜拜~

作业

我把PPT里的题目也放在这里，应该没问题。哔哩哔哩上有作业讲解的。

最后，如有错误，欢迎指出。以及，欢迎关注公众号“我是陈小白”。