递归排序和归并排序算法及其复杂度分析以及小和问题
#include
using namespace std;
void swap(int arr[], int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
void merge(int arr[],int left,int middle,int right) {
if (arr == nullptr)
return;
int left_ptr = left;
int right_ptr = middle+1;
int *res = new int[right-left+1];
int index = 0;
while (left_ptr <= middle && right_ptr <= right) {
if (arr[left_ptr] <= arr[right_ptr]) {
res[index] = arr[left_ptr++];
}
else {
res[index] = arr[right_ptr++];
}
index++;
}
while (left_ptr <= middle) {
res[index] = arr[left_ptr++];
index++;
}
while (right_ptr <= right) {
res[index] = arr[right_ptr++];
index++;
}
for (int i = 0; i < right - left + 1; ++i) {
arr[left+i] = res[i];
}
}
void merge_sort(int arr[],int left,int right) {
if (arr == nullptr||right==left) return;
int middle = (left + right) / 2;
merge_sort(arr,left, middle);
merge_sort(arr, middle + 1, right);
merge(arr,left, middle, right);
}
int main() {
int N;
while (cin >> N) {
int* arr = new int[N];
for (int i = 0; i < N; ++i) {
int temp;
cin >> temp;
arr[i] = temp;
}
merge_sort(arr,0, N-1);
for (int i = 0; i < N; ++i) {
cout << arr[i];
}
cout << endl;
}
}
一、master公式如下图所示
二、递归排序算法
递归排序算法的基本思想:将数组分为左右两半部分,分别在左/右半部分别求局部最大值,然后对这两部分的局部最大值求一个全局最大值。递归实际就是系统不断调用栈记录现场相信和还原现场信息的过程,所以所有的递归算法都可以使用非递归实现。
测试代码:
#include
using namespace std;
int maxTwo(int x, int y)
{
return x > y ? x : y;
}
int getMax(int arr[], int l, int r)
{
if (l == r)
return arr[l];
int mid = (l + r) / 2;
int maxLeft = getMax(arr, l, mid);
int maxRight = getMax(arr, mid + 1, r);
return maxTwo(maxLeft, maxRight);
}
int main()
{
int arr[]{ 1,3,4,2,5 };
int arr_length = sizeof(arr) / sizeof(arr[0]);
cout << getMax(arr, 0, arr_length-1)< 时间复杂度分析:
左右两部分分别是N/2,所以时间复杂度 T(N) = 2T(N/2) + O(1) .O(1)表示最后的maxTwo操作。
更具master公式可知,a = b = 2,d = 0. log(2,2) = 1< 0,所以时间复杂度为O(N).
三、归并算法
1、归并排序基本思路:
先左边排好序,然后右边排好序,然后利用外排的方式进行排序
外排:首先将数组的左右两边排好,准备一个辅助数组arr。然后a指针指向左边第一个,b指针指向右边第一个。如果a比b大,那么a指针不变,移动b指针指向下一个数;如果a比b小,那么b指针不动,移动a指针指向下一个数。谁小谁往辅助数组填,直到a或者b指针移动到最后一个数,然后将剩下的拷贝到辅助数组的后面即可。比如现在a指向3,b指向0,b小,辅助数组第一个填0,然后b移动到下一个,指向1,a不动还是指向3,b比a小,将1填进辅助数组,然后b移动到下一个,指向2,a不动还是指向3,b比a小,将2填进辅助数组,b到尽头,将a剩下的拷贝到辅助数组后面,最后将辅助数组拷贝回原数组,排序完成。
2、外排的复杂度分析
左右两边T(N) = 2T(N/2),a,b指针移动,拷贝到辅助函数O(N),所以T(N) = 2T(N/2)+O(N),利用master公式可得归并排序复杂度为O(N*logN)。
测试代码:
#include
using namespace std;
void merge(int arr[], int L, int mid, int R)
{
//新建一个辅助数组
int* help = new int[R - L + 1];
int i = 0;
//p1和p2分别指向L和mid+1的下标
int p1 = L;
int p2 = mid + 1;
//while实现的就是谁小填谁的过程
while (p1 <= mid && p2 <= R)
//填完之后i和p1,p2小的那个要往下走(++)
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
//到达尽头要将后面的拷贝到help中
while (p1 <= mid)
help[i++] = arr[p1++];
while (p2 <= R)
help[i++] = arr[p2++];
//最后将辅助数组拷贝回原数组
for (i = 0;i < _msize(help) / sizeof(help[0]); i++)
arr[L+i] = help[i];
}
void sortProcess(int arr[], int L, int R)
{
if (L == R)
return;
int mid = L + ((R - L) >> 1);//等价于(L+R)/2
sortProcess(arr, L, mid);//T(N/2)
sortProcess(arr, mid + 1, R);//T(N/2)
merge(arr, L,mid,R);//O(N)
//T(N) = 2T(N/2)+O(N)
}
int main()
{
int array[] = { 1,3,4,2,5 };
int array_length = sizeof(array) / sizeof(array[0]);
sortProcess(array, 0, array_length - 1);
for (int i = 0; i < array_length; i++)
cout << array[i] << " ";
cout << endl;
system("pause");
} 输出:1 2 3 4 5
五、小和问题
1、最直接的思路
这里提供一个简单的思路就是直接将每 i 位置的数和前面的数逐个做比较,如果前面的数小就将他们加起来。很显然下面的测试代码是的时间复杂度是O(N^2)。这个测试代码可以用于当作对数器的检验函数。
测试代码:
#include
using namespace std;
int smallSum(int arr[], int arr_length)
{
int sum = 0;
//i从0位置往右增加
for (int i = 0; i < arr_length; i++)
//j从i位置往左减少
for (int j = i; j > 0; j--)
//注意每次都是和i位置比较
if (arr[i] > arr[j - 1])
sum += arr[j - 1];
return sum;
}
int main()
{
int array[] = {3,5,4,6};
int array_length = sizeof(array) / sizeof(array[0]);
int result = smallSum(array, array_length);
cout << result << endl;
system("pause");
}
2、归并算法的思路
左边排序的时候产生小和,右边排序产生小和,最后merge的时候产生小和,res = 他们的和。其实代码和归并排序的差不多,但是这里会加上前一个博客提到的对数器检验算法的好坏,那个准确无误正确的算法采用前面那个简单的思路的代码。
测试代码:
#include
using namespace std;
int merge(int arr[], int l,int mid, int r)
{
int* help = new int[r - l + 1];
int i = 0;
int p1 = l;
int p2 = mid + 1;
int res = 0;
while (p1 <= mid && p2 <= r)
{
//产生小和的过程,如果p1比p2小,那么产生(r - p2 + 1)个arr[p1]小和
res += arr[p1] < arr[p2] ? (r - p2 + 1)*arr[p1] : 0;
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= mid)
help[i++] = arr[p1++];
while (p2 <= r)
help[i++] = arr[p2++];
for (i = 0; i < _msize(help) / sizeof(help[0]); i++)
arr[l + i] = help[i];
return res;
}
int mergeSort(int arr[], int l, int r)
{
if (l == r)
return 0;
int mid = l + ((r - l) >> 1);
return mergeSort(arr, l, mid) + mergeSort(arr, mid + 1, r) + merge(arr, l, mid, r);
}
int smallSum(int arr[], int arr_length)
{
if (arr == NULL || arr_length < 2)
return 0;
return mergeSort(arr, 0, arr_length - 1);
}
int main()
{
int array[] = { 3,5,4,6 };
int array_length = sizeof(array) / sizeof(array[0]);
int result = smallSum(array, array_length);
cout << result << endl;
system("pause");
}
利用对数器测试算法:
#include
#include //提供sort
#include //提供rand()
using namespace std;
int merge(int arr[], int l, int mid, int r);
int mergeSort(int arr[], int l, int r);
int smallSum(int arr[], int arr_length);
int len(int* arr);
int comparator(int arr[], int arr_length);
int* generateRandomArray(int size, int value);
int* copyArray(int arr[], int arr_length);
int main()
{
int testTime = 3;
int maxSize = 10;
int maxValue = 100;
bool succeed_flag = true;
for (int i = 0; i < testTime; i++)
{
//产生一个随机数组arr1
int* arr1 = generateRandomArray(maxSize, maxValue);
int arr1_length = len(arr1);
//复制这个随机数组到arr2
int* arr2 = copyArray(arr1, arr1_length);
int arr2_length = len(arr2);
int result_1 = smallSum(arr1, arr1_length);
int result_2 = comparator(arr2, arr2_length);
if (result_1 == result_2)
cout << "Nice" << endl;
else
cout << "Fuck~" << endl;
}
system("pause");
}
int merge(int arr[], int l, int mid, int r)
{
int* help = new int[r - l + 1];
int i = 0;
int p1 = l;
int p2 = mid + 1;
int res = 0;
while (p1 <= mid && p2 <= r)
{
//产生小和的过程,如果p1比p2小,那么产生(r - p2 + 1)个arr[p1]小和
res += arr[p1] < arr[p2] ? (r - p2 + 1)*arr[p1] : 0;
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= mid)
help[i++] = arr[p1++];
while (p2 <= r)
help[i++] = arr[p2++];
for (i = 0; i < _msize(help) / sizeof(help[0]); i++)
arr[l + i] = help[i];
return res;
}
int mergeSort(int arr[], int l, int r)
{
if (l == r)
return 0;
int mid = 1 + ((r - l) >> 1);
//返回左侧排序产生的小和+右侧产生的小和+merge过程中产生的小和
return mergeSort(arr, 1, mid) + mergeSort(arr, mid + 1, r) + merge(arr, l, mid, r);
}
int smallSum(int arr[], int arr_length)
{
if (arr == NULL || arr_length < 2)
return 0;
return mergeSort(arr, 0, arr_length - 1);
}
//动态数组的长度求法
int len(int* arr)
{
int arr_length = (int)_msize(arr) / sizeof(arr[0]);
return arr_length;
}
//这个是用来检测算法的函数,就是前面那个简单思路时间复杂度为O(N^2)的算法
int comparator(int arr[], int arr_length)
{
int sum = 0;
for (int i = 0; i < arr_length; i++)
for (int j = i; j > 0; j--)
if (arr[i] > arr[j - 1])
sum += arr[j - 1];
return sum;
}
//这个函数是生成随机数组的函数,返回的是指向数组的指针
int* generateRandomArray(int size, int value)
{
//rand()%10产生的伪随机数为0-9,rand()%10/10.0产生的是[0,1)的小数,(size+1)与之相乘的结果就是产生[0,size]大小的随机数
//这里产生的array的数组的大小就是 一个随机的大小,但是肯定在[0,size]内
int arr_length = (int)((size + 1)*(rand() % 10 / 10.0));
int* array = new int[arr_length];
for (int i = 0; i < arr_length; i++)
{
//数组中的每一值也是随机的,两个随机数减一下,有负也有正。
array[i] = (int)((value + 1)*(rand() % 10 / 10.0)) - (int)((value + 1)*(rand() % 10 / 10.0));
}
return array;
}
//将数组复制一次,返回复制后的数组名(地址)
int* copyArray(int arr[], int arr_length)
{
if (arr == NULL)
return NULL;
int* res = new int[arr_length];
for (int i = 0; i < arr_length; i++)
res[i] = arr[i];
return res;
}
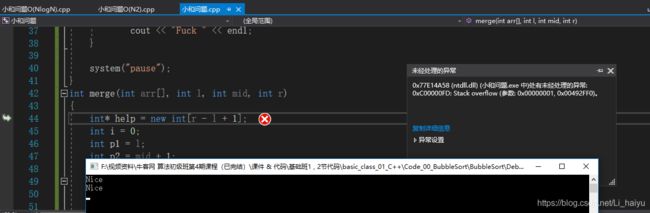
输出显示执行到第三次报错如下Stack Overflow,暂时还没有找到问题解决办法[捂脸]~