LeetCode 自由之路（动态规划、回溯法）

视频游戏“辐射4”中，任务“通向自由”要求玩家到达名为“Freedom Trail Ring”的金属表盘，并使用表盘拼写特定关键词才能开门。
给定一个字符串 ring，表示刻在外环上的编码；给定另一个字符串 key，表示需要拼写的关键词。您需要算出能够拼写关键词中所有字符的最少步数。
最初，ring 的第一个字符与12:00方向对齐。您需要顺时针或逆时针旋转 ring 以使 key 的一个字符在 12:00 方向对齐，然后按下中心按钮，以此逐个拼写完 key 中的所有字符。
旋转 ring 拼出 key 字符 key[i] 的阶段中：
您可以将 ring 顺时针或逆时针旋转一个位置，计为1步。旋转的最终目的是将字符串 ring 的一个字符与 12:00 方向对齐，并且这个字符必须等于字符 key[i] 。
如果字符 key[i] 已经对齐到12:00方向，您需要按下中心按钮进行拼写，这也将算作 1 步。按完之后，您可以开始拼写 key 的下一个字符（下一阶段）, 直至完成所有拼写。
示例：

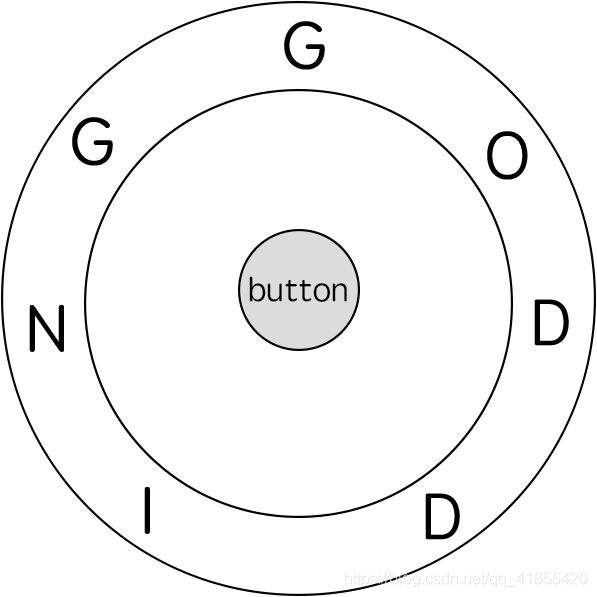
输入: ring = "godding", key = "gd"
输出: 4
解释:
 对于 key 的第一个字符 'g'，已经在正确的位置, 我们只需要1步来拼写这个字符。 
 对于 key 的第二个字符 'd'，我们需要逆时针旋转 ring "godding" 2步使它变成 "ddinggo"。
 当然, 我们还需要1步进行拼写。
 因此最终的输出是 4。

提示：

ring 和 key 的字符串长度取值范围均为 1 至 100；
两个字符串中都只有小写字符，并且均可能存在重复字符；
字符串 key 一定可以由字符串 ring 旋转拼出。

思路分析： 该开始，想着回溯法，就是每次将key[index]寻找ring[nextLocation]，从nowLocation到达nextLocation有顺时针、逆时针两种转法，每次选择最小值。一直搜索，知道拼写除了key。

class Solution {
public:
	int minRes = INT_MAX, ringSize = 0;
	int findRotateSteps(string ring, string key) {
		ringSize = ring.size();
		vector<pair<int, vector<int>>> ringCh(26);//ringCh[ch - 'a']储存字符ch在ring中的各个index
		//统计ring中各个字符出现的下标
		for (int index = 0; index < ringSize; ++index) {
			ringCh[ring[index] - 'a'].second.push_back(index);
		}
		dfs(ringCh, ring, key, 0, 0, 0);//开始搜索
		return minRes;
	}
    //nowIndex是即将拼写的key中的下标，nowSteps到达此时的步骤数，nowLocation现在所处的下标
	void dfs(vector<pair<int, vector<int>>> &ringCh, string &ring, string &key, int nowIndex, int nowSteps, int nowLocation) {
		int keySize = key.size();
		if (nowIndex == keySize) {//完成搜索
			minRes = min(nowSteps, minRes);
		}
		else {
            //搜索下一步的位置
            for (auto nextLocation : ringCh[key[nowIndex] - 'a'].second) {
                //顺时针、逆时针转动，选择较小者
                int minSteps = min((ringSize + nowLocation - nextLocation) % ringSize, (ringSize + nextLocation - nowLocation) % ringSize);
                if (minSteps + nowSteps + 1 < minRes) {
                    //如果key在nowIndex存在连续的重复字母，直接按buttonStep次
                    int tempIndex = nowIndex, buttonStep = 0;
                    while (tempIndex < keySize && key[tempIndex] == key[nowIndex]) {
                        tempIndex += 1;
                        buttonStep += 1;
                    }
                    dfs(ringCh, ring, key, tempIndex, nowSteps + minSteps + buttonStep, nextLocation);
                }
            }
		}
	}
};

回溯法，没有找到高效的剪枝就TM是暴搜。。。
方法二：动态规划法。
二维数组dp，其中dp[i][j]表示转动从i位置开始的key串所需要的最少步数(这里不包括spell的步数，因为spell可以在最后统一加上)，此时表盘的12点位置是ring中的第j个字符。我们可以从key的末尾往前推，这样dp[0][0]就是我们所需要的结果，因为此时是从key的开头开始转动，而且表盘此时的12点位置也是ring的第一个字符。
现在我们来看如何找出递推公式，对于dp[i][j]，我们知道此时要将key[i]转动到12点的位置，而此时表盘的12点位置是ring[j]，我们有两种旋转的方式，顺时针和逆时针，我们的目标肯定是要求最小的转动步数，而顺时针和逆时针的转动次数之和刚好为ring的长度n，这样我们求出来一个方向的次数，就可以迅速得到反方向的转动次数。
为了将此时表盘上12点位置上的ring[j]转动到key[i]，我们要将表盘转动一整圈，当转到key[i]的位置时，我们计算出转动步数diff，然后计算出反向转动步数，并取二者较小值为整个转动步数step，此时我们更新dp[i] [j]，更新对比值为step + dp[i+1][k]， 这个也不难理解，因为key的前一个字符key[i+1]的转动情况suppose已经计算好了，那么dp[i+1][k]就是当时表盘12点位置上ring[k]的情况的最短步数，step就是从ring[k]转到ring[j]的步数，也就是key[i]转到ring[j]的步数，
用语言来描述就是，从key的i位置开始转动并且此时表盘12点位置为ring[j]的最小步数(dp[i][j])就等价于将ring[k]转动到12点位置的步数(step)加上从key的i+1位置开始转动并且ring[k]已经在表盘12点位置上的最小步数(dp[i+1][k])之和。

class Solution {
public:
    int findRotateSteps(string ring, string key) {
        int n = ring.size(), m = key.size();
        vector<vector<int>> dp(m + 1, vector<int>(n));//dp[i][j]代表从字符ring[j]的位置转到字符key[i]的位置需要的转动次数（不包括拼写）
        for (int i = m - 1; i >= 0; --i) {
            for (int j = 0; j < n; ++j) {
                dp[i][j] = INT_MAX;
                //表盘转动一整圈，当转到key[i]的位置时，我们计算出转动步数diff，然后计算出反向转动步数，并取二者较小值为整个转动步数step，此时我们更新dp[i][j]
                for (int k = 0; k < n; ++k) {
                    if (ring[k] == key[i]) {
                        int diff = abs(j - k);
                        int step = min(diff, n - diff);
                        dp[i][j] = min(dp[i][j], step + dp[i + 1][k]);//更新
                    }
                }
            }
        }
        return dp[0][0] + m;//最后的m是key单词拼写次数
    }
};

方法二：带备忘录的回溯法。（思路和没有通过的回溯法一致）

class Solution {
public:
    int findRotateSteps(string ring, string key) {
        int n = ring.size(), m = key.size();
        vector<vector<int>> v(26);
        vector<vector<int>> memo(n, vector<int>(m, 0));
        for (int i = 0; i < n; ++i) {
            v[ring[i] - 'a'].push_back(i);
        }
        return helper(ring, key, 0, 0, v, memo);
    }
    int helper(string ring, string key, int x, int y, vector<vector<int>>&v, vector<vector<int>>& memo) {
        if (y == key.size()) return 0;
        if (memo[x][y]) {//如果搜索过，直接返回
            return memo[x][y];
        }
        int res = INT_MAX, n = ring.size();
        //搜索从ring[x]的位置转到字符key[y]的位置需要的转动次数
        for (int k : v[key[y] - 'a']) {
            int diff = abs(x - k);
            int step = min(diff, n - diff);
            res = min(res, step + helper(ring, key, k, y + 1, v, memo));
        }
        return memo[x][y] = res + 1;
    }
};