高等代数---欧几里得空间

高等代数–欧几里得空间

声明： 本篇文章内容主要对《高等代数》第三版第九章内容的总结，复习

定义与基本性质

线性运算：在线性空间中,向量之间的基本运算只有加法与数量乘法,统称为线性运算。
度量性质：如长度、夹角等。
内积和外积的定义需要注意。
欧式空间是特殊的线性空间，所以类似的满足线性空间的一些性质。

定义1：设V是实数域R上一线性空间,在V上定义一个二元实函数,称为内积,记作(α,β),它具有以下性质：
1(α,β)=(β,α)
2)(kα,β)=k(α,β)
3)(α+β,γ)=(β,γ)+(α,γ)
4)(α,α)≥0,当且仅当α=0时(α,α)=0
这里α,β,γ是V中任意的向量,k是任意实数,这样的线性空间V称为欧几里得空间
注意：两个不同的内积构成两个不同的欧几里得空间

注意：
1.只有零向量的长度才为零。
2.长度为1的向量称为单位向量
3.α/|α| 称为把 α单位化



定义4：如果向量α,β的内积为零,即
（α,β）=0
那么α,β称为正交或互相垂直,记为α⊥β。


注意：度量矩阵是正定的。
欧几里得空间简称欧式空间。

标准正交基

定义5：欧氏空间V中一组非零的向量,如果它们两两正交,就称为一正交向量组
注意：
1.正交向量组是线性无关的
2.单个非零的向量所成的向量组也是正交向量组

定义6：在n维欧氏空间中,由n个向量组成的正交向量组称为正交基;由单位向量组成的正交基称为标准正交基。
注意：
1.对一组正交基进行单位化就得到一组标准正交基。
2.一组基为标准正交基的充分必要条件是:它的度量矩阵为单位矩阵
3.在n维欧式空间中，标准正交基是存在的。
4.所有的标准正交基，在欧式空间中有相同的地位。

定理1：n维欧氏空间中任一个正交向量组都能扩充成一组正交基

下面的例子非常具有代表意义。


注意： 请务必注意上边的公式(5)和公式(6)，这是标准正交基到标准正交基过度的关键。
定义7: n级实数矩阵A称为正交矩阵,如果A^TA=E
具有以下性质：
1.|A|=±1
2.标准正交基到标准正交基的过渡矩阵是正交矩阵
3.第一组基是标准正交基,同时过渡矩阵是正交矩阵,那么第二组基一定也是标准正交基
4.A^T =A^-1

同构

说明：说实话，同构的作用除了引出变换的概念，并没有看出其他的作用。

从上面的定义第3点中可以看出，还是和前面的概念有点不一样的，主要是为了保证内积不变。
注意：
1.同构的欧式空间必有相同的维数。
2.每个n维的欧式空间都与Rⁿ 同构。
3.同构作为欧式空间之间的关系具有反身性，对称性，与传递性。

定理3：两个有限维欧氏空间同构的充分必要条件是它们的维数相同

正交变换

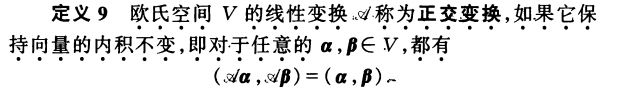
注意：
1.正交矩阵的乘积与正交矩阵的逆矩阵也是正交矩阵
2.第一类的—旋转(正交变换)，|A|=1,第二类正交变换(镜面反射)，|A|=-1

子空间

实对称矩阵的标准型

引理1：设A是实对称矩阵,则A的特征值皆为实数

注意：这块的例子还是比较经典的，多看一下例子更加的帮助去理解。

向量到子空间的距离·最小二乘法

、

最小二乘法的例子看一下还是非常有用的

酉空间介绍

详细看书P390页

链接: 更多高等代数内容点击此处.
参考书籍：《高等代数》第三版 王萼芳 石生明 修订 高等教育出版社