广度搜索bfs

    广度搜索在acm中应用十分广泛，英文简写是BFS(breadth first search)。

下面先看一下例子：

在一个4*4的矩形中，有一些位置设置有障碍，要求从(1,1)走到(4,4),求最短距离。

分析：假设没有任何障碍，我们可以走的路线如下：

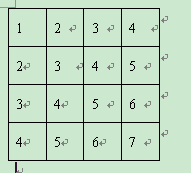
起点为(1,1)，假设这一步是第一步可以到达的位置；然后它可以向相邻的方向走一步，

如向右或向下就到达2号位置，2号就代表从起点到这个位置要走两步；3又是2号走一步；

4是3走一步；这样子就像从1号展开以水波，向四周扩散，我们只要把这些相邻的位置

全部保存在队列中，就会遍历完相邻的区域。

下面通过一个具体的例子讲一下如何编程实现：

问题：

南阳理工学院校园里有一些小河和一些湖泊，现在，我们把它们通一看成水池，假设有一张我们学校的某处的地图，这个地图上仅标识了此处是否是水池，现在，你的任务来了，请用计算机算出该地图中共有几个水池。

输入：

第一行输入一个整数N，表示共有N组测试数据
每一组数据都是先输入该地图的行数m(0<m<100)与列数n(0<n<100)，然后，输入接下来的m行每行输入n个数，表示此处有水还是没水（1表示此处是水池，0表示此处是地面）

输出：

输出该地图中水池的个数。
要注意，每个水池的旁边（上下左右四个位置）如果还是水池的话的话，它们可以看做是同一个水池。

下面是程序的源代码：

#include<stdio.h>

#include<iostream>

#include<queue>



using namespace std;



struct Point

{

    int x;

    int y;

};



int dir[4][2]={{0,1},{1,0},{0,-1},{-1,0}};//分别表示向四个方向做一步

int main()

{

    queue<Point> que;//保存相连的一片水池

    Point p1,p2;

    int cnt;

    scanf("%d",&cnt);

    while(cnt--)

    {

        int m,n;

        scanf("%d %d",&m,&n);

        bool check[101][101]={false};//全部没有访问过

        int map[100][100];

        int i,j;

        int count=0;//水池个数

        for(i=0;i<m;i++)

            for(j=0;j<n;j++)

            {

                scanf("%d",&map[i][j]);

            }//for(j)

        for(i=0;i<m;i++)

            for(j=0;j<n;j++)

            {

                if(map[i][j]==1&&check[i][j]==false)//遇到一个新的水池

                {

                    p1.x=i;

                    p1.y=j;

                    que.push(p1);//当前点如队列

                    ++count;//发现一个就加1

                    check[p1.x][p1.y]=true;

                    while(que.empty()==false)  //把相连的全部如对列，只要队列不空，继续找相连的

                    {

                        p1=que.front();//取出头

                        que.pop();//每次都要弹出,但是不一定会有进去的，所以会结束



                        int k;

                        for(k=0;k<4;k++)  //四个方向

                        {

                            p2.x=p1.x+dir[k][0];

                            p2.y=p1.y+dir[k][1];



                            if(p2.x<0||p2.x>=m||p2.y<0||p2.y>=n)//超出范围

                            {

                                continue;

                            }

                            if(map[p2.x][p2.y]==1&&check[p2.x][p2.y]==false)

                            {

                                check[p2.x][p2.y]=true;

                                que.push(p2);

                            }

                        }//for

                    }//while

                    

                }//if





            }//for(i)

            cout<<count<<endl;

    }

    

    return 0;

}

注意：

1：遍历时要把相邻的水池算成一个，那么就要向四个方向同步搜索，设置一个dir[4][2]数组，

分别加上这个数组的值，就代表了向四个方向的遍历。

2:广度搜索的思想就是从一个地方向四周搜，我们把这个中心放到队列里，然后把所有相邻的

也同时加到队列里，并且访问过的做个标记(check[i][j]=true)，这样就能确保全部遍历。

 

 

问题2：亡命逃窜  http://acm.nyist.net/JudgeOnline/problem.php?pid=523

下面是源程序：

#include<stdio.h>

#include<queue>



using namespace std;

struct unit

{

    int step;

    bool check;

};



unit maze[51][51][51];//存放路径

struct point

{

    int x;

    int y;

    int z;

};



int dir[6][3]={{1,0,0},{0,1,0},{0,0,1},{-1,0,0},{0,-1,0},{0,0,-1}};//分别向六个方向搜索



int main()

{

    int i,j,k;

    int cnt;

    scanf("%d",&cnt);

    while(cnt--)

    {

        int a,b,c,t;

        scanf("%d %d %d %d",&a,&b,&c,&t);

        for(i=0;i<a;i++)

            for(j=0;j<b;j++)

                for(k=0;k<c;k++)

                {

                    scanf("%d",&maze[i][j][k].step);

                    maze[i][j][k].check=false;

                }



        bool reachdoor=false;

        bool outtime=false;

        

        point p1,p2;

        queue<point> que;

        //必然是一条连通的路，所以只要一个节点进入队列，就能遍历所有的节点

        int step=0;

        p1.x=p1.y=p1.z=0;

        maze[p1.x][p1.y][p1.z].step=0;//两个参数都在入队的时候设置;没有这一步就wrong

        maze[p1.x][p1.y][p1.z].check=true;

        que.push(p1);

        while(!que.empty()&&!reachdoor&&!outtime)

        {

            p1=que.front();

            que.pop();            

            step=maze[p1.x][p1.y][p1.z].step;

            if(step>t)

            {

                outtime=true;

                break;

            }

            if(p1.x==a-1&&p1.y==b-1&&p1.z==c-1)//到门口

            {

                reachdoor=true;

                break;

            }

            int m;

            for(m=0;m<6;m++)

            {

                p2.x=p1.x+dir[m][0];

                p2.y=p1.y+dir[m][1];

                p2.z=p1.z+dir[m][2];

                if(p2.x<0||p2.y<0||p2.z<0||p2.x>=a||p2.y>=b||p2.z>=c)

                {

                    continue;

                }//if

                

                if(!maze[p2.x][p2.y][p2.z].check&&maze[p2.x][p2.y][p2.z].step==0)//没有检查且是路

                {

                    maze[p2.x][p2.y][p2.z].check=true;

                    maze[p2.x][p2.y][p2.z].step=step+1;                    

                    que.push(p2);

                }

            }//for(m)            

        }//while(que)

        if(reachdoor&&!outtime)

            printf("%d\n",step);

        else

            printf("-1\n");        

    }//while(cnt--)

    return 0;

}

分析：

(1)这个题编程立体形状；需要向六个方向遍历。

(2)不是像水池一样，这题求最短路径，因为有时间限制，所以只需要把一个点入队列，就可以

遍历所有的节点。

(3)有关节点的信息，如check,step都要在push之前设置，要不就会出错。

(4)逻辑关系，如超时、到点终点、队列为空，都是循环结束的条件，把这些条件放到外面，

内层只需要根据条件等级break，或者push。