数学建模之Hermite插值法和三次样条插值法(附上详细的matlab代码)
插值算法
一般定义
若P(x)为次数不超过n的代数多项式,即
P ( x ) = a 0 + a 1 x + . . . + a n x n P(x)=a_0+a_1x+...+a_nx^n P(x)=a0+a1x+...+anxn
- 若P(x)为分段多项式,即分段插值
- 若P(x)为三角多项式,即三角插值(一般用到傅里叶变换等复杂的数学工具)
拉格朗日插值法
在若干个不同的地方得到的观测值,拉格朗日插值发可以找到一个多项式,恰好在各个观测点取到观测值。
拉格朗日插值函数:(存在缺陷)
L n ( x ) = ∑ i = 0 n y i ( ∏ j = 0 j ≠ i n x − x j x i − x j ) L_n(x)=\sum_{i=0}^{n}y_i(\prod_{j=0\\j≠i}^{n}{\frac{x-x_j}{x_i-x_j}}) Ln(x)=i=0∑nyi(j=0j=i∏nxi−xjx−xj)
上述方法存在着龙格现象(Runge phenomemon),由下图可知:
高次插值会产生龙格现象,在两端的波动极大,产生明显的震荡。在不熟悉曲线运动趋势的前提下,尽量不要使用高次插值。
牛顿插值法
f ( x ) = f ( x 0 ) + f [ x 0 , x 1 ] ( x − x 0 ) + f [ x 0 , x 1 , x 2 ] ( x − x 0 ) ( x − x 1 ) + . . . + f [ x 0 , x 1 , . . . , x n − 1 , x n ] ( x − x 0 ) . . . ( x − x n ) f(x)=f(x_0)+f[x_0,x_1](x-x_0)\\ +f[x_0,x_1,x_2](x-x_0)(x-x_1)+...\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +f[x_0,x_1,...,x_{n-1},x_n](x-x_0)...(x-x_n) f(x)=f(x0)+f[x0,x1](x−x0)+f[x0,x1,x2](x−x0)(x−x1)+... +f[x0,x1,...,xn−1,xn](x−x0)...(x−xn)
差商:
称 f [ x 0 , x k ] = f ( x k ) − f ( x 0 ) x k − x 0 为 f ( x ) 关 于 x 0 , x k 的 一 阶 差 商 称f[x_0,x_k]=\frac{f(x_k)-f(x_0)}{x_k-x_0}为f(x)关于x_0,x_k的一阶差商\\ 称f[x0,xk]=xk−x0f(xk)−f(x0)为f(x)关于x0,xk的一阶差商
二阶差商:
f [ x 0 , x 1 , x 2 ] = f [ x 0 , x 2 ] − f [ x 0 , x 1 ] x 2 − x 1 f[x_0,x_1,x_2]=\frac{f[x_0,x_2]-f[x_0,x_1]}{x_2-x_1} f[x0,x1,x2]=x2−x1f[x0,x2]−f[x0,x1]
k阶差商:
f [ x 0 , x 1 , . . . , x k ] = f [ x 1 , . . . , x k − 1 , x k ] − f [ x 0 , x 1 , . . . , x k − 1 ] x k − x 0 f[x_0,x_1,...,x_k]=\frac{f[x_1,...,x_{k-1},x_k]-f[x_0,x_1,...,x_{k-1}]}{x_k-x_0} f[x0,x1,...,xk]=xk−x0f[x1,...,xk−1,xk]−f[x0,x1,...,xk−1]
两种插值法的对比
由于牛顿插值法每次插值只和前n项的值有关,每次只要在原来的函数上添加新的项,产生新的函数
故牛顿插值法具有继承性,但仍存在龙格现象。
为了应对数学建模比赛,我们基本上用的是以下两种插值方法:
① 分段三次埃尔米特(Hermite)插值法
直接使用Hermite插值算法得到的多项式次数较高时,存在龙格现象,因此实际使用中,一般使用分段三次Hermite插值多项式。(PCHIP)
Matlab中的内置函数:
% x为已知样本点的横坐标,y是已知样本点的纵坐标
% new_x是要插入处对应的横坐标,返回p为new_x带入插值多项式下的值
p = pchip(x,y,new_x)
②三次样条插值法
三次样条插值生成的曲线更加光滑
% x为已知样本点的横坐标,y是已知样本点的纵坐标
% new_x是要插入处对应的横坐标,返回p为new_x带入插值多项式下的值
p = spline(x,y,new_x)
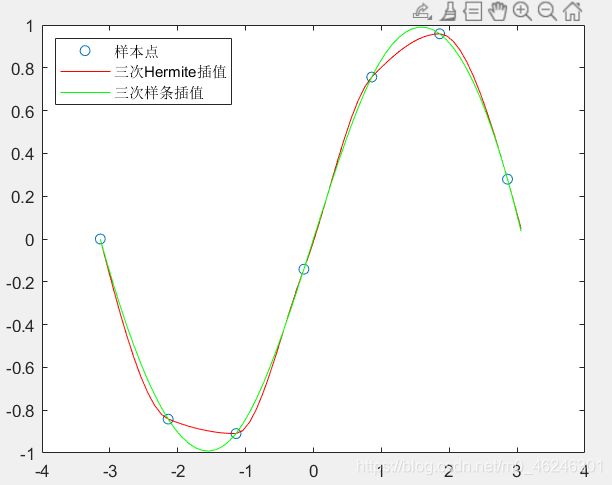
下面比较这两种插值法:
clc,clear;
x = -pi:pi;
y = sin(x);
new_x = -pi:0.1:pi;
% 分段三次Hermite插值
p1 = pchip(x,y,new_x);
% 三次样条插值
p2 = spline(x,y,new_x);
figure(1);
plot(x,y,'o',new_x,p1,'r-',new_x,p2,'g-');
legend('样本点','三次Hermite插值','三次样条插值','Location','NorthWest')
在预测模型中,可以使用以上插值法进行预测:
clc,clear;
load population.mat
year = 2009:2018;
% 分段三次Hermite插值预测
p1 = pchip(year, A, 2018:2021);
% 三次样条插值预测 (更加平滑)
p2 = spline(year, A, 2018:2021);
figure(2);
plot(year,A,'o--',2018:2021,p1,'r*-',2018:2021,p2,'bx-')
n维数据的插值法
p = interpn(x1, x2,..., xn, y, new_x1, new_x2,..., new_xn, method)
% x2,x2,...,xn为已知样本点的横坐标
% y是已知样本点的纵坐标
% new_x1,new_x2,...,new_xn是插入点的横坐标
% method:
% 'linear':线性插值
% 'cubic':三次插值
% 'spline':三次样条插值法(最精准)
% 'nearest':最邻近插值法
p = interpn(x,y,new_x,'spline');
% 等价于
p = spline(x,y,new_x); % 更加光滑,连续
clc,clear;
load A1.mat
load A2.mat
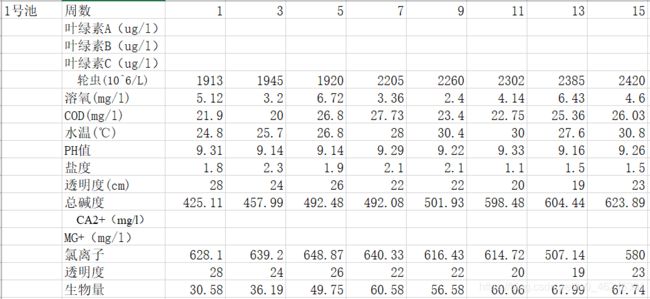
x = 1:2:15;
y_label={'周数','轮虫','溶氧','COD','水温','PH值','盐度','透明度','总碱度','氯离子','透明度','生物量'};
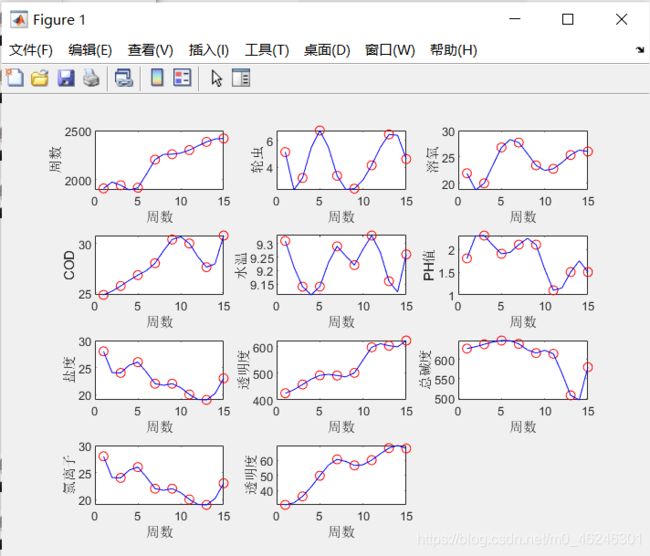
for i = 1:11
y = A1(i,:);
new_x = 1:15;
p = spline(x,y,new_x);
disp(p);
subplot(4,3,i);
plot(x,y,'ro',new_x,p,'b-');
% axis([0,15,-inf,inf])
xlabel('周数');
ylabel(y_label{i});
end
参考资料:数学建模清风:论文写作方法课程 https://www.bilibili.com/video/BV1Na411w7c2