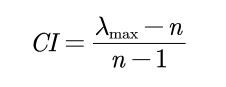数学建模学习笔记(一) 层次分析法
数学建模学习笔记 (一) 层次分析法
文章目录
- 数学建模学习笔记 (一) 层次分析法
- 前言
- 一、层次分析法
- 二、问题引入
-
- 1.评价类问题
- 2.评价类问题解决方法
- 3.实例
-
- 判断矩阵
- 一致矩阵
- 一致性检验
- 判断矩阵计算权重
-
- 方法1:算术平均法求权重
- 方法2:几何平均法求权重
- 方法3:特征值法求权重
- 通过权重矩阵计算得分
- 三、层次分析法的局限
- 四、总结
前言
此系列文章主要记录在学习数学建模过程中的知识点和自己的理解,如果出错请多多指正。
学习的教材和资源主要来源与清风的讲解视频,想全面了解可移步清风:数学建模算法、编程和写作培训的视频课程以及Matlab等软件教学
一、层次分析法
—————————————————————————————
层次分析法(The Analytic Hierarchy Process即 AHP)是在充分研究了人类思维过程 的基础上提出来的,它较合理地解决了定性问题定量化的处理过程
其主要用于解决评价类问题(例如:选择哪种方案更好,哪位同学表现更好)
—————————————————————————————
二、问题引入
1.评价类问题
当我们要评价一个方案的好坏,一个事物的优劣时,往往要有一个指标来评判而不是按照主观的印象来进行评价。
例如评价一个方案是否好时,可以通过对方案中涉及的花费因素,创新因素进行打分,来确定方案的优劣。
故评价类问题,常用的解决方法是对其打分从而选出最优
—————————————————————————————
2.评价类问题解决方法
面对评价类问题我们首先要确定好三个主要方面
1)我们评价的目标是什么
2)我们拥有的多少种方案去达到预期的目标
3)我们根据什么去评判方案的好坏
举一个简单的例子:
评判奖学金通过学习成绩和课外成绩来决定,有两位同学争夺奖学金,那就要对两位同学的课内成绩和课外成绩进行打分,综合成绩高者当然就获得了奖学金。
其中课内成绩对奖学金的重要程度占比90%,课外成绩占比%10.
| 指标权重 | 小明 | 小王 | |
|---|---|---|---|
| 课内成绩 | 0.9 | 0.6 | 0.4 |
| 课外成绩 | 0.1 | 0.7 | 0.3 |
(课内成绩中的0.6和0.4分别表示,小明和小王相比,小明课内得分为0.6,小王0.4,0.7和0.3同理)
我们可以通过数据可以很容易得到这个表格且由此计算出小明和小王的综合得分
小明:0.6 * 0.9 + 0.7 * 0.1= 0.61
小王:0.4 * 0.9 + 0.3 *0.1 = 0.39
可以看到小明最后应该得到奖学金,这就是一个最基础的评价类问题,下面举一个较为真实且有代表性的评价类问题,加深理解且引出我们的层次分析法的思想
—————————————————————————————
3.实例
这里引用清风视频中的例子来说明评价类问题的实际解决方法
例:小明同学想出去旅游。在查阅了网上的攻略后,他初步选择
了苏杭、北戴河和桂林三地之一作为目标景点。请你确定评价指标、形成评价体系来为小明同学选择最佳的方案。
**首先我们来回答面对评价类问题的三个主要方面:
1)我们评价的目标是什么——为小明选取最佳的旅游地点
2)我们拥有多少种方案去达到预取目标——苏杭,北戴河和桂林
3)我们根据什么去评判方案的好坏——题目没有数据提供给我们具体的判断标准,这个情况需要我们通过搜索数据或者文献去制定一个评价标准。如本例中我们选取①景点景色,②旅游花费,③居住环境,④饮食情况,⑤交通便利情况,五个判断指标去评价好坏**
当我们确定好我们三个问题答案后,我们就需要通过确定的判断指标去选择方案从而达到我们的目标。
而我们第现在要解决的第一个问题,如果确定像上个例子中,每个指标对方案的指标权重。
这个所谓的指标权重,确定的方法有很多,但在本例中,我们通过层次分析法的思想来确定每个指标的权重
—————————————————————————————
判断矩阵
这里我们引入判断矩阵来辅助我们确定权重,我们用1-9来表示重要程度,我们通过两两比较每个指标的重要程度来构造判断矩阵
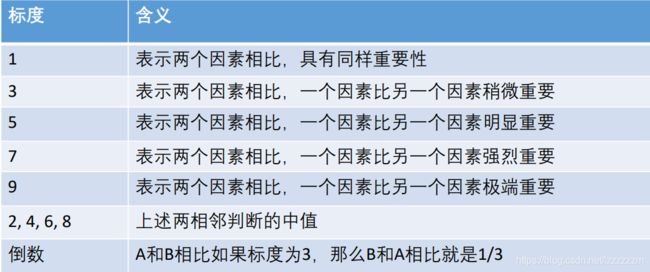
假设我们人为的已经通过比较确定好了两两之间的重要程度,并填表可得下图
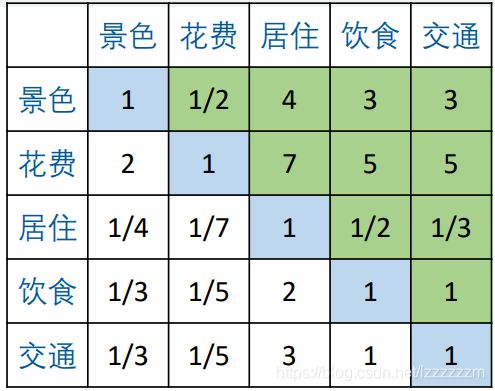
上图即为我们构造的表格,我们将此称作判断矩阵
表格解释:在此简单的解释表格的含义
(花费,景色)= 2 ,表明花费比景色稍微重要一些,重要程度为2
(景色,居住)= 4,表明景色比居住重要一些,重要程度为4
而当我们构造完判断矩阵后,就可以利用此来计算我们的指标权重
—————————————————————————————
一致矩阵
在这之前我们还需要定义一个概念:一致矩阵
至于为什么要定义一致矩阵,个人理解为,我们填写判断矩阵时,有很大的人为因素,而来通过检验我们构造的判断矩阵的一致性可以一定情况下减少这种主观性,增加客观性。
—————————————————————————————
一致性检验
进行一致性检验有三个步骤
| 表示判断矩阵特征值的最大值 | |
|---|---|
| n | 一致矩阵的秩 |
3)计算一致性比例CR
其中CR<0.1,则可以认为判断矩阵的一致性可以接受,否则需要对判断矩阵进行修改
—————————————————————————————
判断矩阵计算权重
当我们判断矩阵进行完一致性检验后,如果其一致性可以接受,则可以对判断矩阵进行计算权重
计算判断矩阵的权重有三种方法
方法1:算术平均法求权重
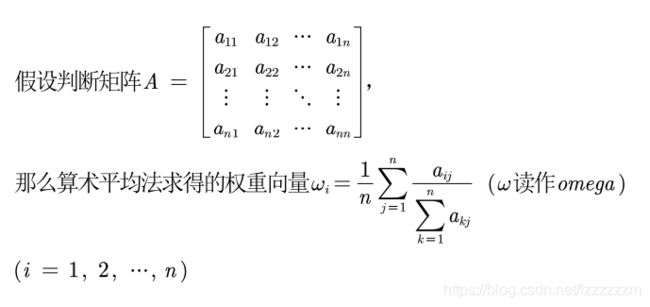
第一步:将判断矩阵按照列归一化——每一个元素除以其所在列的和
第二步:将归一化的各列相加(按行求和)
第三步:将相加后得到的向量中每个元素除以n即可得到权重向量
方法2:几何平均法求权重
第一步:将A的元素按照行相乘得到一个新的列向量
第二步:将新的向量的每个分量开n次方
第三步:对该列向量进行归一化即可得到权重向量
方法3:特征值法求权重
第一步:求出矩阵A的最大特征值以及其对应的特征向量
第二步:对求出的特征向量进行归一化即可得到我们的权重
—————————————————————————————
通过权重矩阵计算得分
我们通过上述方法计算得到权重后,可以得到各个指标的权重及其占比,从而得到下述矩阵,称为权重矩阵
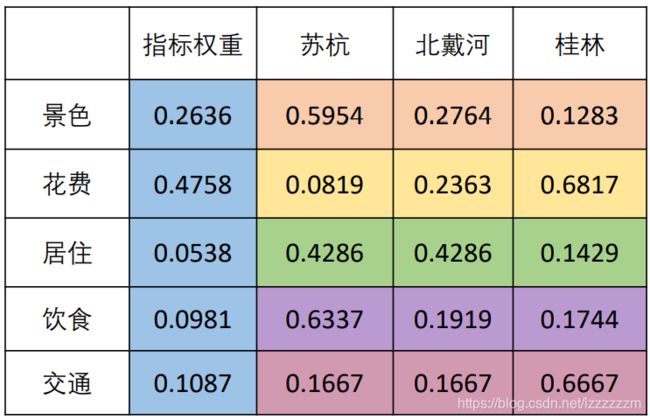
我们可以通过此来计算方案的得分:
苏杭:0.5954 * 0.2636 + 0.0819 * 0.4758 + 0.4286 * 0.0538 + 0.6337 * 0.0981 + 0.1667 * 0.1087 = 0.299
类似的,我们可以得到北戴河得分为0.245,桂林得分为0.455.因此最佳的旅游景点是桂林
自此我们就利用层次分析法选择除了我们的方案解决了问题。
—————————————————————————————
三、层次分析法的局限
1)评价的准则不能太多,太多的话n会很大,判断矩阵和一致矩阵差异可能会很大。
2)如果准则层中指标的数据是已知的,我们就不能自己瞎填判断矩阵 了
—————————————————————————————
四、总结
对于评价类问题,我们可以采用层次分析法进行打分评价解决问题
其中步骤有:
1)分析系统中各因素之间的关系,建立系统的递阶层次结构
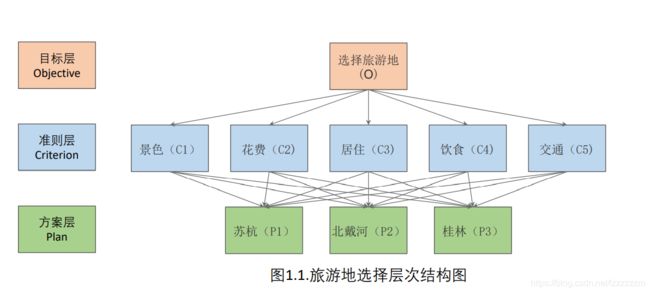
2)对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较,构造两两比较矩阵(判断矩阵)。
如上图:
准测层中的元素要两两比较对目标层的重要性来构造判断矩阵,从而构造出准则层对于目标层的权重
方案层中的元素两两比较对准测层中每个元素的重要性来构造判断矩阵,从而确定方案层对于每个准则层的权重
3)由判断矩阵计算被比较元素对于该准则的相对权重,并进行一致性检验(检验通过权重才能用).
计算权重时,建议三种方法都使用,可以保证结果的稳健性
在一致性检验中,上述说过,如果CR>0.1则不通过,这时需要人为的去修改判断矩阵,向一致矩阵靠拢(比较判断矩阵就是人为填的)
填写技巧:一致矩阵每行成比例
4)根据权重矩阵计算得分,并进行排序