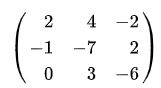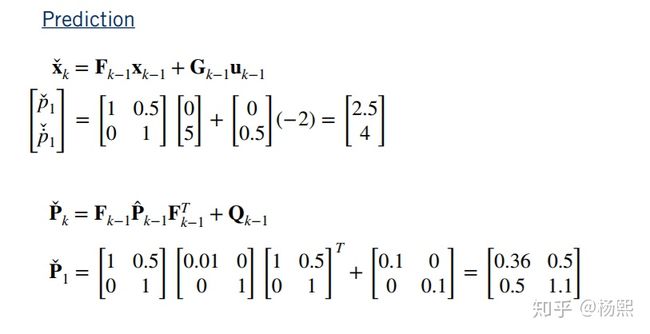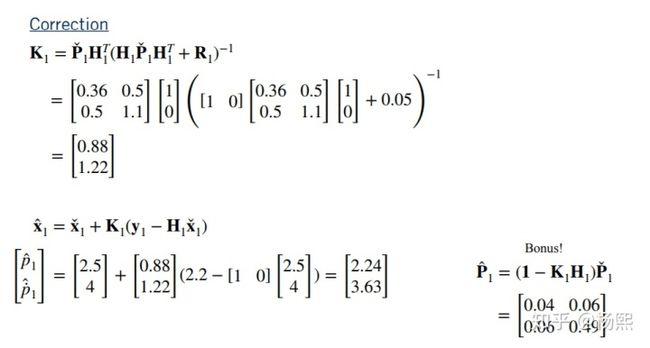最小二乘估计_人工智能背后的数学-入门:线性代数的几何意义,最小二乘和状态估计最基本概念...
前言
这是受某重要人物之约,于2.3日晚上进行的一场技术直播的讲义(相当于PPT了)。主要介绍内容余下:
1. 线性代数的几何意义: 向量的几何意义,矩阵的秩,矩阵的行列式的值 到底有什么几何意义。特征向量和特征值又对应什么?
2. 概率论里的几个重要的基本概念,均值方差,协方差,协方差矩阵。大数定律和中心极限定律。尤其是协方差矩阵是非常重要的概念。
3. 最小二乘法-最简单的"机器学习"。 这是一切人工智能的起点。300多年过去了,依然不失光彩。从几何和微积分两个角度推导最小二乘法。
4. 权重最小二乘法->迭代最小二乘法->Kalman滤波和状态估计介绍->kalman滤波在姿态估计,无人驾驶中的应用(如果有时间的话)
5. 优秀书籍,优秀网站及教育平台推荐。
本文的很多内容都是在我以前学习的时候总结看到的一些优秀教程上借鉴过来的。
[所有内容在2020.2.3日晚上前会持续更新添加中。。。]
向量内积和叉积
点积(内积):
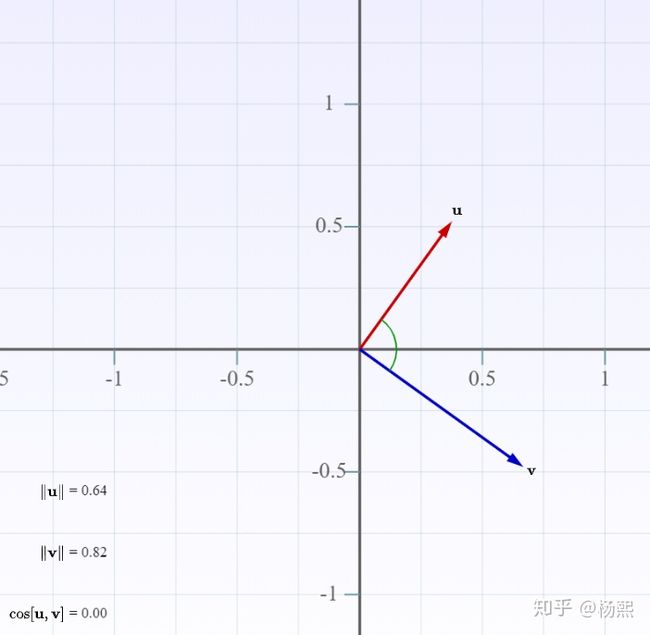
点积有很多物理解释:比如物理上代表做工,如果两个向量是单位向量,那么点积就是两个向量的夹角,向量的夹角可以代表两个向量的方向的差异。。。
点积被定义为一个标量:
-
(代数公式)
-
(几何意义,做功,或者说叫投影)
两个正交向量的点积为0,这也是垂直(正交是垂直的多维推广)的定义
此处为互动动画叉积(外积):
外积只能定义在三维空间上
代数计算:
几何意义:
三重矢量积公式:http://immersivemath.com/ila/ch04_vectorproduct/ch04.html
矩阵
矩阵从解线性方程组而来:
抽象为系数矩阵:
解线性方程的过程抽象为高斯消元法。(这思想很朴素嘛!早生400年,我们也能想到。。)
关于rank的其他内容讲解: http://immersivemath.com/ila/ch06_matrices/ch06.html
矩阵行列式
•几何意义:行列式中行或列向量所构成超平行多面体的有向面积或有向体积,另一个解释是矩阵A的行列式是线性变化A下的图形面积或体积的伸缩因子
关于rank的其他内容讲解:http://immersivemath.com/ila/ch07_determinants/ch07.html
矩阵的秩
- 任何矩阵空间的维数等于列空间的维数等于矩阵的秩
- 8对于所有矩阵,不相关的行数 = 不想关的列数等于秩
- 非满秩矩阵(变换之后维度跌落了!) <=> 不可逆矩阵<=>奇异矩阵<=>行列式为0
关于rank的其他内容讲解: http://immersivemath.com/ila/ch08_rank/ch08.html
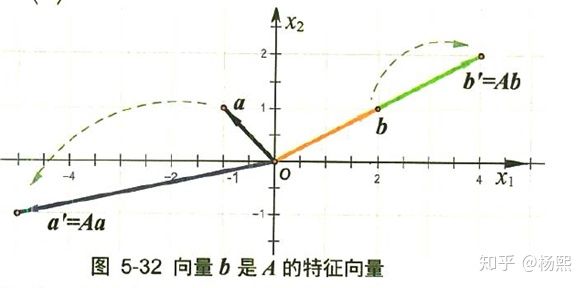
特征值与特征向量
关于rank的其他内容讲解: http://immersivemath.com/ila/ch10_eigen/ch10.html
第二部分-最小二乘法(LS),递归最小二乘法(RLS)
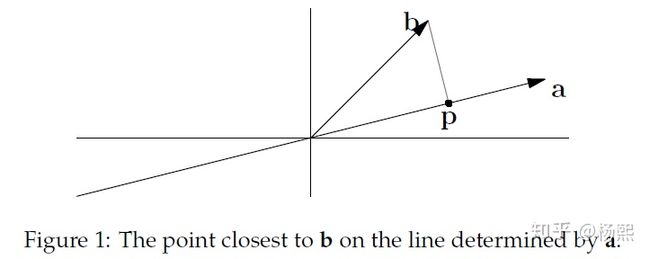
几何解释及推导:
拓展到高维空间:
最小二乘法应用与多维的情况,最小二乘公式,务必牢记!!!栗: 三点直线拟合:
代数形式推导LS:
1801年1月,天文学家Giuseppe Piazzi发现了一颗从未见过的小行星。据说刚发现不久,他就病倒了,等病好时,已过了几个月,那颗小行星却怎么也找不到了。当时有名的天文学家都加入了对这颗小行星的寻找,却徒劳无获。
1801年9月,高斯决定用数学方法寻找这颗小行星的踪迹。3个月后,高斯宣称已预测出该小行星的轨道。天文学家在高斯指出的位置,果然再次发现了它。这颗小行星后来被命名为谷神星(Ceres)。高斯因为此事名声大震,但他却拒绝透露计算小行星轨道的办法;8年后,直到高斯系统地完善了相关的数学理论,才将他的方法公布于众,这就是“最小二乘法”(Least squares method)。
最小二乘法普遍用于回归分析,例如根据以往观察到的行星位置,预测它的运行轨道。最小二乘法跟矩阵理论有着某种神秘的联系。
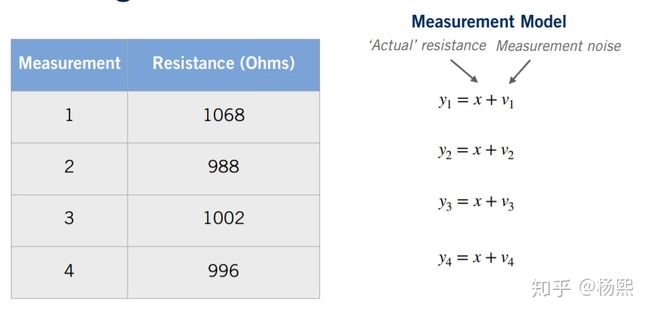
设我们用万用表测量电阻阻值, 4次测量结果如下表,模型为简单的线性模型:
误差可以写作如下形式:
最小二乘即希望:
先说答案:
导数为0点为极值点:
推导(利用求导):
展开可得:
为求极值,令导数为0:
最小二乘解为:
最小二乘互动演示:https://phet.colorado.edu/sims/html/least-squares-regression/latest/least-squares-regression_en.html
互动演示2:https://textbooks.math.gatech.edu/ila/least-squares.html
最小二乘法有几个限制(缺点)
- 最小二乘法只能解决线性问题,模型必须是线性
- 最小二乘法假设所有测量的权重都是一样的。不会更相信哪次测量或者更不相信哪次测量。
权重最小二乘(WLS)
WLS是LS的推广。最小二乘的一个确定就是所有的测量都是相同权重的,我们现在必须考虑有的测量要你其他测量好 或者 坏的情况。我们需要给每次测量增加权重。
我们用每个测量值的方差来描述对每次测量的信任程度,那么新的误差函数就变成了:
求出解的过程和LS是一样的,还是求导:
WLS的解:
下面是一个例子,还是万用表测电阻,这次用两个万用表,一个是低精度的,一个高精度的,低精度的
下面是一个LS 和 WLS 的损失函数,解和限制条件对比:
最小二乘的结果等价于噪声为高斯白噪声时的最大似然估计法
是的,还是高斯发现的。。假设误差服从高斯分布:
为什么要假设为高斯白噪声:
中心极限定理的互动直观解释:http://mfviz.com/central-limit/
递归最小二乘(RLS-Recursive Least Squares)
还是上面的例子,如果万用表每秒都可以测量一次电阻值,那怎么用最小二乘? 不可能把所有的值都存起来然后做一次最小二乘,那样运算量巨大,所以只能求其次。实时来进行最小二乘,怎么做呢?
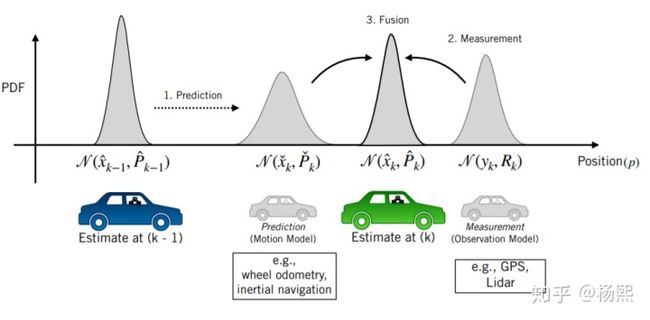
我们需要一个线性递归估计器,他每一步都根据上一步的最佳估计来寻找当前的最佳估计值
递推公式为:
总结一下:系统方程:
怎么求K?给个常数,不行,K需要实时变化调整:
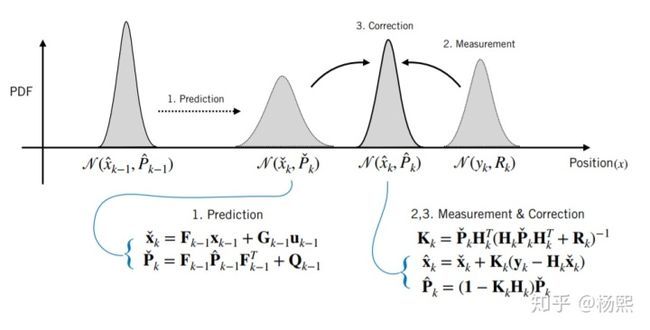
在RLS中,不再把误差当做优化目标,而是把每个状态量的方差作为优化目标RLS公式为:
最终算法如下:
例子,使用RLS估计电阻值:
对应代码:
clc;
clear;
I = [0.2 0.3 0.4 0.5 0.6];
V = [1.23 1.38 2.06 2.47 3.17];
% batch soluction
H = [I', ones(5, 1)];
x_ls = (H'*H)^(-1)*H'*V';
% Recursive Estimator
P = diag([10^(2), 0.2^(2)]);
x = [9 0]';
% record history of state varible
x_hist(1,:) = x;
num_meas = length(I);
R = 0.0225;
for i = 1:num_meas
H = [I(i), 1];
K = P*H'*(H*P*H' + R)^(-1);
x = x + K*(V(i) - H*x);
P = (eye(2) - K*H)*P;
x_hist(i,:) = x;
end
plot(I,V, '.-')
hold on;
grid on;
plot(I, I*x_ls(1) + x_ls(2) )
hold on;
plot(I, x_hist(:,1)'.*I + x_hist(:,2)', '*')
legend('measurement','LS','RLS');
ylabel('V')
xlabel('I')
title('LS&RLS')Kalman滤波器
Kalman是2016年才去世的。。。https://www.zhihu.com/video/1207659782112477184优秀网站及教育平台推荐
- MITOpenCourseWare
- Coursera
- Udacity优达学城
- GIthub
参考资料
- Cousera 自动驾驶课程:https://www.coursera.org/learn/state-estimation-localization-self-driving-cars
- 中心极限定理的互动直观解释:http://mfviz.com/central-limit/
- B站3B1B系列数学课程:https://space.bilibili.com/88461692?from=search&seid=2560814780683895117
- MIT 线性代数课程:https://ocw.mit.edu/courses/mathematics/18-06sc-linear-algebra-fall-2011