信号处理第二式——计算两个序列的时间延迟MTALAB代码实现讲解
信号处理第二式——计算两个序列的时间延迟
文章目录
- 信号处理第二式——计算两个序列的时间延迟
- 一、计算算法
- 二、代码实现
-
- 1.非周期信号计算时间延迟
- 2.周期信号计算时间延迟
提示:以下是本篇文章正文内容。
一、计算算法
计算两个序列的时间延迟通常使用如下两种算法:快速线性相关算法和循环相关算法
设两个有限长序列x(n),n=0,.,N-1和y(n),n=0,1…,M- 1,相关长度L=N+M-1
(1)快速线性相关算法实现
①为防止循环卷积发生混叠,首先将x(n)和y(n)补零到等于L或大于L(保证L为2的幂次方,便于基2的FFT运算),得到x1(n)和y1(n)。
②用FFT算法计算x1(n)和y2(n)的DFT变换得X1(k)和Y2(k) :
③利用循环卷积定理得到线性相关
④对结果做适当的修正得到相关序列Rxy(n)
(2)循环相关算法
与快速线性算法相比,设置了延迟序列,取更少的点,计算速度大大减少,效率得到了提升。
二、代码实现
1.非周期信号计算时间延迟
例:从 delaydatal. txt文件读人两通道数据,分别设为x和y。它们
之间的延迟量为54个样点,以xcorr、快速线性相关和循环相关计算延迟量,比较它们的结果。
代码如下:
% 例:从 delaydatal. txt文件读人两通道数据,分别设为x和y。它们
% 之间的延迟量为54个样点,以xcorr、快速线性相关和循环相关计算延迟量,比较它们的结果。
xx=load('delaydata1.txt'); %载入数据
x=xx(:,1); %读取第一列的数据
y=xx(:,2); %读取第二列的数据
[Rxy,lags]=xcorr(y,x); %用xcorr函数计算线性相关
N=length(x); %获取数据长度
%快速计算线性相关
X=fft(x,2*N);
Y=fft(y,2*N);
Sxy=Y.*conj(X); %得到互相关
sxy=ifftshift(ifft(Sxy)); %ifft 调整序列顺序
Cxy=sxy(2:end); %只取2*N-1个点
subplot 211;
line(lags,Rxy,'linewidth',4);hold on
plot(lags,Cxy,'k');
axis([-100 100,-50 200]);
legend('xcorr函数得到','快速线性相关得到');
xlabel('样点');
ylabel('相关函数幅值');
title('两种方法线性相关求延迟量');
%循环相关
Xc=fft(x);
Yc=fft(y);
Scxy=Yc.*conj(Xc);
scxy=ifftshift(ifft(Scxy)); %ifft 调整序列顺序
Ccxy=scxy(2:end); %只取N-1个点
lagc=-N/2+1:N/2-1;
subplot 212;
plot(lagc,Ccxy,'k');
axis([-100 100,-50 200]);
xlabel('样点');
ylabel('相关函数幅值');
title('循环相关方法求延迟量');
结果图可见无论是快速线性相关还是循环相关算法,求得到的延迟量都是54个样点。因为delaydata1为振动信号,周期性不强,所以循环相关算法可以使用。

2.周期信号计算时间延迟
例:从 delaydata3. txt文件读入两通道数据,分别设为x和y.它们
是矩形脉冲,两序列之间的延迟量为14个样点,以xcorr线性相关和循环相关计算延迟量,并
比较它们的结果。(delaydata3.txt为周期信号)
代码如下:
% 例:从 delaydata3. txt文件读入两通道数据,分别设为x和y.它们
% 是矩形脉冲,两序列之间的延迟量为14个样点,以xcorr线性相关和循环相关计算延迟量,并
% 比较它们的结果。(delaydata3.txt为周期信号)
xx=load('delaydata3.txt'); %载入文件
x=xx(:,1); %获取第一列数据
y=xx(:,2); %获取第二列数据
N=length(x); %获取长度
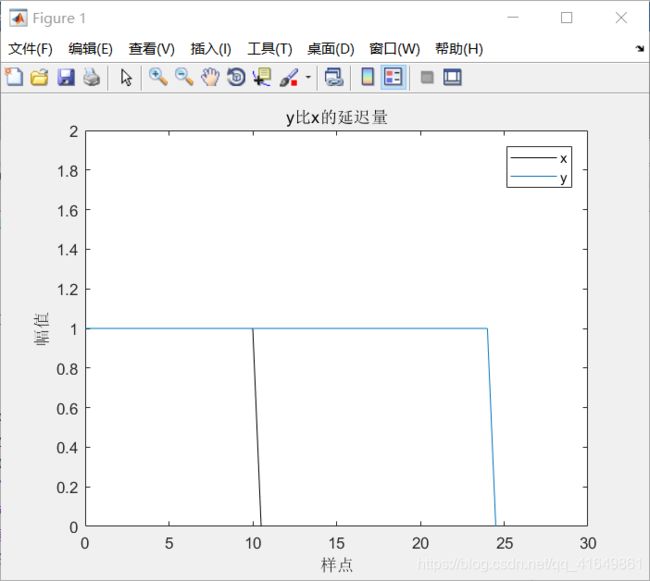
plot(0:N-1,x,'k');hold on
plot(0:N-1,y);
axis([0 30,0 2]);
legend('x','y');
xlabel('样点');
ylabel('幅值');
title('y比x的延迟量');
Xc=fft(x);
Yc=fft(y);
%循环相关
Sxy=Yc.*conj(Xc);
sxy=ifftshift(ifft(Sxy));
Cxy=sxy(2:end);
lagc=-N/2+1:N/2-1;
%作图
figure,subplot 311;
plot(lagc,Cxy,'k');
title('x和y的循环相关');
xlabel('样点(a图)');
ylabel('相关函数幅值');
%线性相关
[Rxy,lags]=xcorr(y,x);
%作图
subplot 312;
plot(lags,Rxy,'k');
title('x和y的快速线性相关');
xlabel('样点(b图)');
ylabel('相关函数幅值');
subplot 313;
plot(lags,Rxy,'k');
title('x和y的快速线性相关');
xlabel('样点(c图)');
ylabel('相关函数幅值');
axis([0 50,-1000 1000]);
结果如下图:Figure1可以看出y比x延迟了14个样点,Figure2中用的a图是用循环相关的方法,无法找到最大峰值来确定延迟量;而b图使用快速线性相关算法则可以找到,c图为b图的方法版。可以看出在14的点得到最大峰值。
所以当信号为周期性信号时,不能使用循环相关的算法来获取两个序列的延迟量。

到这本篇博客就结束啦,喜欢的话麻烦一键三连哈!不定期更新信号处理、单片机,传感器的博客,谢谢各位大佬同仁的支持!