屠榜!Swin Transformer !
各种视觉Transformer互相赛高,微软亚洲研究院的Swin Transformer开源了!该模型在分类、检测等多个任务上屠榜!
文章标题:Swin Transformer: Hierarchical Vision Transformer using Shifted Windows
论文地址:https://arxiv.org/abs/2103.14030
代码地址:Swin Transformer
目录
-
- 1 概述
- 2 贡献
- 3 内容
-
- 3.1 总体结构
- 3.2 基于移动窗口的自注意力
- 3.3 模型变种
- 3.4 实验
- 4 总结
1 概述
从ViT出现以来,各种视觉Transformer模型层出不穷,但是几乎所有的Transformer模型都面临一个问题——难以训练、效率低,当数据量不够庞大时它们相对CNN体现不出优势,这对微型实验室极其不友好。而近期微软亚洲研究院提出的Swin Transformer开启了屠榜模式,在图像分类、目标检测和语义分割上稳居榜首,其实这些新方法稳居榜首见怪不怪,重要的是Swin Transformer相比于ViT,计算复杂度大幅下降,可以作为视觉任务的通用Backbone,4月13日凌晨Swin Transformer开源了,备受关注。
众所周知,Transformer原来用于NLP领域,但是它迁移到视觉领域时并没有像大家期望的那么全能那么强大,作者认为这是因为CV和NLP两个领域/模态存在较大差异,比如视觉信息的scale变化较大,NLP中scale则是固定的,且与文本相比,图像的分辨率要高得多(数据量更大,计算量更大),且自注意力的计算复杂度是图像尺寸的平方,图片分辨率增加时这会大幅增加计算量。为了克服上述问题,作者提出了一个通用的Transformer backbone——Swin Transformer,它构造分层的feature maps,而且对图像的尺寸具有线性计算复杂度。
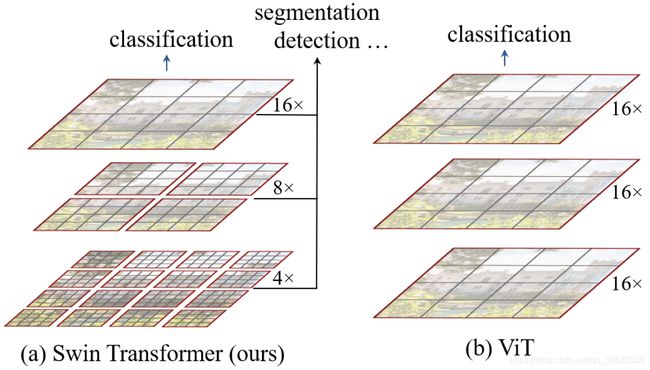
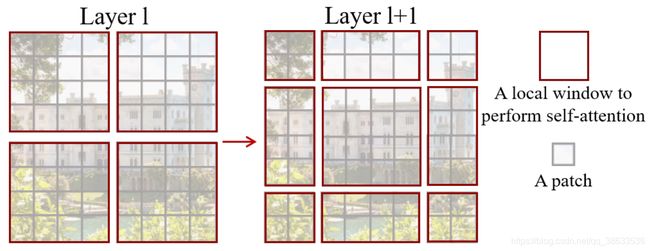
如上图所示,从小尺寸patches(灰色线条)开始,在更深的层中逐步将相邻小patches整合为window(红色线条)以构建分层特征表示,最后计算的是这些非重叠window的局部自注意力,每个window中的patch数量是固定的,所以计算量和图像尺寸呈线性关系,说到这里还有点含糊,后续将进一步介绍。作者说Swin Transformer的关键是窗口分区的shift,下图是计算shift window自注意力方法,在 l l l层,采用规则的窗口划分方案,并在每个窗口中计算自注意力,在 l + 1 l+1 l+1层,窗口划分偏移,这样自注意力的计算就牵扯上了 l l l层中的window的边界,这样就能实现先前窗口之间的连接,显著增强了建模能力,作者后续也用消融实验证明了这一点。
2 贡献
- 提出了Swin Transformer backbone,与输入图像尺寸具有线性复杂度;
- 验证了基于shift window的自注意力的有效性。
3 内容
3.1 总体结构
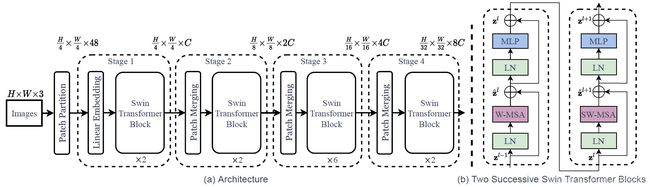
上图是Swin Transformer的tiny版本(Swin-T),一开始和ViT一样将输入的RGB图像分割为不重叠的patch,每个patch都被视为token,其特征为原始像素RGB值的拼接,作者将patch大小设为 4 × 4 4\times 4 4×4,因此每个patch的特征尺寸为 4 × 4 × 3 4 \times 4 \times 3 4×4×3,在原始特征值上做一个线性映射,可以投影到任意维度 C C C,这些和ViT基本一致,做线性映射是为了让输入Transformer的数据维度不受patch数量/尺寸的影响。Swin Transformer block (即修改了自注意力计算的Transformer block)应用于这些patch tokens,token的数量为 H 4 × W 4 \frac{H}{4}\times \frac{W}{4} 4H×4W,与线性嵌入一起构成Stage 1。为了产生分层表示,随着网络变深,使用patch merging层减少token的数量,第1个patch merging层连接每组 2 × 2 2\times 2 2×2相邻patches的特征,然后在 4 C 4C 4C维的连接特征上应用线性层,token的数量将会变为原来的 1 2 × 2 = 4 \frac{1}{2\times2=4} 2×2=41,即 H 8 × W 8 \frac{H}{8}\times \frac{W}{8} 8H×8W,输出维度为 H 8 × W 8 × 2 C \frac{H}{8}\times \frac{W}{8} \times2C 8H×8W×2C,首个patch merging层和Swin Transformer block组成Stage 2,重复两次作为Stage 3和Stage 4,输出维度分别为 H 16 × W 16 × 4 C \frac{H}{16}\times \frac{W}{16} \times4C 16H×16W×4C和 H 32 × W 32 × 8 C \frac{H}{32}\times \frac{W}{32} \times8C 32H×32W×8C,比较好理解,基本思想就是合并patch,当成一个更大的patch,从而减少patch数量,减少计算量。
Swin Transformer block:上图中(b)是Swin Transformer block结构,用shift window模块替换掉原始block中的多头自注意力(MSA)即可,其它层不变,就是Layer normalization和MLP(2个linear层夹一个GELU)。
3.2 基于移动窗口的自注意力
Self-attention in non-overlapped windows:为了更有效地建模,作者建议在局部窗口内计算自注意力,窗口被设定为以非重叠方式均匀分割图像,假设每个窗口包含 M × M M \times M M×M个patches,那么一个全局MSA模块和一个基于 h × w h\times w h×w patches的窗口的计算复杂度为式(1),忽略了 s o f t m a x softmax softmax的复杂度,很显然能够看出前者是patch数量 h w hw hw的二次方,而后者和 h w hw hw呈线性关系。
Ω ( M S A ) = 4 h w C 2 + 2 ( h w ) 2 C Ω ( W − M S A ) = 4 h w C 2 + 2 M 2 h w C (1) \begin{array}{l} \Omega(\mathrm{MSA})=4 h w C^{2}+2(h w)^{2} C \\ \Omega(\mathrm{W}-\mathrm{MSA})=4 h w C^{2}+2 M^{2} h w C \end{array}\tag{1} Ω(MSA)=4hwC2+2(hw)2CΩ(W−MSA)=4hwC2+2M2hwC(1)
Shifted window partitioning in successive blocks:基于窗口计算自注意力降低了计算复杂度,但是窗口与窗口却不能够互相连接,为了在保持非重叠窗口高效计算的同时引入跨窗口连接,作者提出了一种在连续Swin Transformer块中交替进行两个划分配置的shift window(移位窗口)划分方法。就像本文第2张图所示,第1个模块采用从左上角像素开始的规则窗口划分策略,将 8 × 8 8\times 8 8×8的特征均匀划分为 2 × 2 2\times2 2×2的窗口,每个窗口的尺寸是 4 × 4 4\times 4 4×4 (M=4),下一个模块在上一个模块窗口的基础上移动 ( ⌊ M 2 ⌋ , ⌊ M 2 ⌋ ) \left(\left\lfloor\frac{M}{2}\right\rfloor,\left\lfloor\frac{M}{2}\right\rfloor\right) (⌊2M⌋,⌊2M⌋)个像素,语言描述比较含糊,具体还是看图。利用shift window划分方法,连续的Swin Transformer blocks被计算为:
z ^ l = W − M S A ( L N ( z l − 1 ) ) + z l − 1 z l = M L P ( L N ( z ^ l ) ) + z ^ l z ^ l + 1 = S W − MSA ( L N ( z l ) ) + z l z l + 1 = M L P ( L N ( z ^ l + 1 ) ) + z ^ l + 1 , (2) \begin{array}{l} \hat{\mathbf{z}}^{l}=\mathrm{W}-\mathrm{MSA}\left(\mathrm{LN}\left(\mathbf{z}^{l-1}\right)\right)+\mathbf{z}^{l-1} \\ \mathbf{z}^{l}=\mathrm{MLP}\left(\mathrm{LN}\left(\hat{\mathbf{z}}^{l}\right)\right)+\hat{\mathbf{z}}^{l} \\ \hat{\mathbf{z}}^{l+1}=\mathrm{SW}-\operatorname{MSA}\left(\mathrm{LN}\left(\mathbf{z}^{l}\right)\right)+\mathbf{z}^{l} \\ \mathbf{z}^{l+1}=\mathrm{MLP}\left(\mathrm{LN}\left(\hat{\mathbf{z}}^{l+1}\right)\right)+\hat{\mathbf{z}}^{l+1}, \end{array}\tag{2} z^l=W−MSA(LN(zl−1))+zl−1zl=MLP(LN(z^l))+z^lz^l+1=SW−MSA(LN(zl))+zlzl+1=MLP(LN(z^l+1))+z^l+1,(2)
其中 z ^ l \hat{\mathbf{z}}^{l} z^l和 z l \mathbf{z}^{l} zl分别表示block l l l的(S)W-MSA模块和MLP模块的输出特征,W-MSA和SW-MSA表示基于窗口的多头自注意力,分别使用规则划分和shift window划分。
Efficient batch computation for shifted configuration:移动窗口划分方案虽然能减少计算量,但还存在一个问题——窗口的数量会增多,从 ⌈ h M ⌉ × ⌈ w M ⌉ \left\lceil\frac{h}{M}\right\rceil \times\left\lceil\frac{w}{M}\right\rceil ⌈Mh⌉×⌈Mw⌉到 ( ⌈ h M ⌉ + 1 ) × ( ⌈ w M ⌉ + 1 ) \left(\left\lceil\frac{h}{M}\right\rceil+1\right) \times \left(\left\lceil\frac{w}{M}\right\rceil+1\right) (⌈Mh⌉+1)×(⌈Mw⌉+1),而且一些窗口的的尺寸会比 M × M M \times M M×M小,一个简单的解决方案是将其填充至 M × M M\times M M×M,在计算注意力时忽略这些填充,但是用这种方法会增加计算量,假设规则分区中窗口数很小如: 2 × 2 2\times 2 2×2,增至 3 × 3 3\times 3 3×3,计算量增加了2.25倍(原文的表述不是很明晰)。于是作者提出了一种向左上方循环移位的方法,如下图:
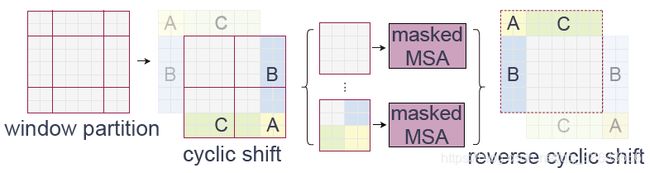
作者最后还加入了Relative position bias,使模型性能得到了提升,这是前人提出的方法。
3.3 模型变种
作者一共介绍了4个版本的模型,Swin-T,Swin-S,Swin-B和Swin-L,其中Swin-B是基础模型,类似ViT-B和DeiT-B,T、S和L三个模型的大小和计算复杂度约是基础模型的 0.25 × , 0.5 × , 2 × 0.25 \times,0.5 \times,2\times 0.25×,0.5×,2×,Swin-T和Swin-S的复杂度分别与ResNet-50和ResNet-101相似,窗口的大小 M = 7 M=7 M=7,每个head的query维度 d = 32 d=32 d=32,每个MLP的扩展层 α = 4 \alpha=4 α=4,具体的模型结构如下, C C C是Stage 1隐层通道数。
Swin-T: C = 96 , layer numbers = { 2 , 2 , 6 , 2 } Swin-S: C = 96 , layer numbers = { 2 , 2 , 18 , 2 } Swin-B: C = 128 , layer numbers = { 2 , 2 , 18 , 2 } Swin-L: C = 192 , layer numbers = { 2 , 2 , 18 , 2 } \begin{array}{l} \text { Swin-T: } C=96 \text { , layer numbers }=\{2,2,6,2\} \\ \text { Swin-S: } C=96 \text { , layer numbers }=\{2,2,18,2\} \\ \text { Swin-B: } C=128 \text { , layer numbers }=\{2,2,18,2\} \\ \text { Swin-L: } C=192 \text { , layer numbers }=\{2,2,18,2\} \end{array} Swin-T: C=96 , layer numbers ={ 2,2,6,2} Swin-S: C=96 , layer numbers ={ 2,2,18,2} Swin-B: C=128 , layer numbers ={ 2,2,18,2} Swin-L: C=192 , layer numbers ={ 2,2,18,2}
3.4 实验
作者将提出的模型用在了图像分类、目标检测和语义分割几个任务上,由于本人的方向与图像分类接近,此处只给出图像分类的单一样例,下图是ImageNet-22K上的分类结果,除了精度外,还可以看出参数量和计算量的差距:
4 总结
总的来说,本文方法的介绍还比较抽象,代码已经开源,可以参考代码,思想很简单,但是一般实验室没有尝试新方法和试错的资本,所以这也是学术路上的障碍。