【Codeforces Global Round 14】Codeforces-1515 ABCD
A. Phoenix and Gold
A题简直绝了。写错几个细节居然过了样例,wa了几发才发现,最后一步忘记输出“YES”,又wa了几发才发现,我菜死了,QAQ
先将数组降序排序,显然的,如果a[0]>x,那么直接输出排序后的数组即可。
降序排序的时候,假若有前k(k
n=5,x=9
5 4 3 2 1
当k=2时,恰好5+4=9 == x,交换后有5 3 4 2 1,此时当k=2时sum
如果k恰好等于n的时候,无法向右交换,那必“NO”。
void solves(){
int n,x;cin>>n>>x;
int sum=0;
for(int i=0;i<n;++i) cin>>a[i];
sort(a,a+n,greater<int>());
if(a[0]>x){
cout<<"YES\n";
for(int i=0;i<n;++i) cout<<a[i]<<" ";cout<<endl;
return ;
}
int flag=0;
for(int i=0;i<n;++i){
sum+=a[i];
if(sum==x){
if(i==n-1){
cout<<"NO\n";return ;
}
swap(a[i+1],a[i]);
break;
}
}
cout<<"YES\n"<<endl;
for(int i=0;i<n;++i) cout<<a[i]<<" ";cout<<endl;
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
int OvO;
cin>>OvO;
// OvO=1;
while(OvO--){
solves();
}
}
B. Phoenix and Puzzle
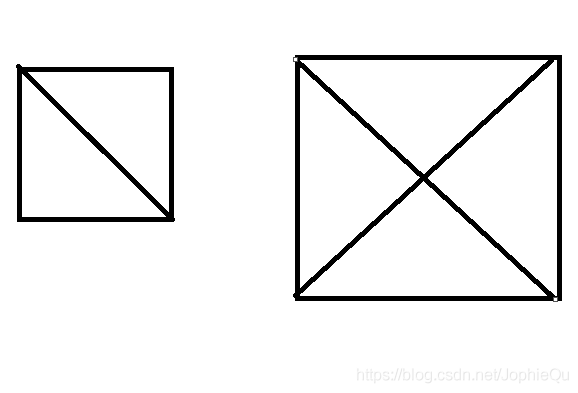
n个三角形构成正方形的充分必要条件为 存在一个正方形可以分割成若n个相同的三角形,我们将这样的正方形称其为合法的。
显然一个合法的正方形可以由m个正方形组成,其中m必为完全平方数。那么任何一个正方形都可以拆成若干个小正方形,一直拆到不能拆为止(即m=1)。我们可以将不能继续拆分的小正方形理解成一个基。
显然的,基只能沿对角线进行拆分。
void solves(){
int n;cin>>n;
if(n&1){
cout<<"NO\n";return ;
}
if(n%2==0){
int m=n/2;
int i=sqrt(m);
if(i*i==m){
cout<<"YES\n";return ;
}
}
if(n%4==0){
int m=n/4;
int i=sqrt(m);
if(i*i==m){
cout<<"YES\n";return ;
}
}
cout<<"NO\n";
}
C. Phoenix and Towers
c题题意看了十几分钟才看懂,果然决定12月才考四级是明智的选择呢OvO
优先队列模拟即可。只是我不熟练,所以没想到。
void solves(){
priority_queue<pair<int,int>>q;
int n,m,x;cin>>n>>m>>x;
for(int i=1;i<=m;++i) q.push({
0,i});
cout<<"YES\n";
while(n--){
int x;cin>>x;
pair<int,int>re;
re=q.top();
q.pop();
cout<<re.second<<" ";
re.first-=x;
q.push(re);
}cout<<endl;
}
D. Phoenix and Socks
为什么我感觉D比C简单QAQ
分别存下左袜子和右袜子的数量,对齐后相消相同的值。说的可能有点抽象,举个栗子:
n=10,l=5,r=5
l = 1 , 1 , 1 , 2 , 4 l=1,1,1,2,4 l=1,1,1,2,4
r = 1 , 2 , 2 , 2 , 3 r=1,2,2,2,3 r=1,2,2,2,3
对齐
i 1 2 3 4 5 l i 3 1 0 1 0 r i 1 3 1 0 0 \begin{array}{c|lcr} i & \text{1} & \text{2} & \text{3} & \text{4} & \text{5}\\ \hline l_i & 3 & 1 & 0 & 1 & 0 \\ r_i & 1 & 3 & 1 & 0 &0\\ \end{array} iliri131213301410500
相消
i 1 2 3 4 5 l i 2 0 0 1 0 r i 0 2 1 0 0 \begin{array}{c|lcr} i & \text{1} & \text{2} & \text{3} & \text{4} & \text{5}\\ \hline l_i & 2 & 0 & 0 & 1 & 0 \\ r_i & 0 & 2 & 1 & 0 &0\\ \end{array} iliri120202301410500
左袜子和右袜子各剩下3,则直接ans=3即可。
还有一种情况是相消后左袜子和右袜子数量不一致:
i 1 2 3 4 5 l i 2 0 0 1 0 r i 0 4 1 0 0 \begin{array}{c|lcr} i & \text{1} & \text{2} & \text{3} & \text{4} & \text{5}\\ \hline l_i & 2 & 0 & 0 & 1 & 0 \\ r_i & 0 & 4 & 1 & 0 &0\\ \end{array} iliri120204301410500
恰好右袜子多了两只。那么显然转移数量>1的右袜子数量过去是最优解。转移过后再相消,此时 a n s + = m i n ( l e n / 2 , r 2 / 2 ) ans+=min(len/2,r_2/2) ans+=min(len/2,r2/2),其中,len为右袜子和左袜子的差值。
i 1 2 3 4 5 l i 2 0 0 1 0 r i 0 2 1 0 0 \begin{array}{c|lcr} i & \text{1} & \text{2} & \text{3} & \text{4} & \text{5}\\ \hline l_i & 2 & 0 & 0 & 1 & 0 \\ r_i & 0 & 2 & 1 & 0 &0\\ \end{array} iliri120202301410500
转移完数量>1的袜子后,如果左袜子和右袜子还是不等,ans+=len/2即可,其中len为左袜子和右袜子的差值。最后ans再加上剩下的袜子总数的一半。
思维很简单,但是代码真的好多细节。。。。我又调了好久orzorzorz
const int N=2e5+7;
int l[N],r[N];
void solves(){
int n,ll,rr;cin>>n>>ll>>rr;
int a;
int sum=n;
memset(l,0,sizeof(l));
memset(r,0,sizeof(r));
for(int i=1;i<=ll;++i){
cin>>a;
++l[a];
}
for(int i=1;i<=rr;++i){
cin>>a;
++r[a];
}
int ans=0;
int m;
for(int i=1;i<=n;++i){
if(r[i]&&l[i]){
m=min(r[i],l[i]);
r[i]-=m;l[i]-=m;
ll-=m;rr-=m;
sum-=2*m;
}
}
if(ll>rr){
int len=ll-rr;
for(int i=1;i<=n;++i){
if(l[i]>1){
int re=min(l[i]/2,len/2);
ans+=re;
len-=re*2;
l[i]-=re*2;
ll-=re*2;
sum-=re*2;
}
if(!len)break;
}
} else if(ll<rr){
int len=rr-ll;
for(int i=1;i<=n;++i){
if(r[i]>1){
int re=min(r[i]/2,len/2);
ans+=re;
len-=re*2;
r[i]-=re*2;
rr-=re*2;
sum-=re*2;
}
if(!len)break;
}
}
ans+=(max(ll,rr)-min(ll,rr))/2;
ans+=sum/2;
cout<<ans<<endl;
}