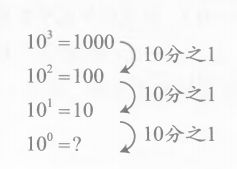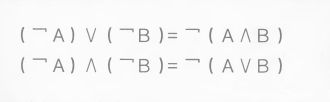《程序员的数学1》读书笔记整理
《程序员的数学》
- 前言
- 0的故事——无即是有
-
- 按位计数法
- 不适用按位计数法的罗马数字
- 指数法则
- 0所起的作用
- 人类的极限和构造的发现
- 逻辑——真与假的二元世界
-
- 乘车费用问题——兼顾完整性和排他性
-
- 有没有遗漏?
- 建立复杂命题
-
- 逻辑非
-
- 双重否定等于肯定
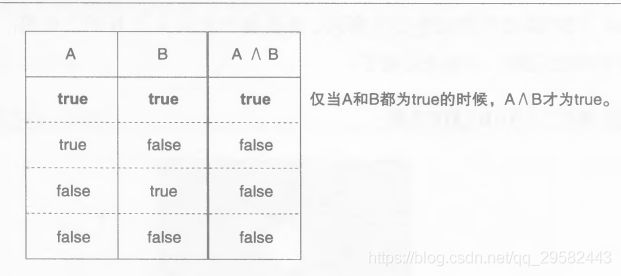
- 逻辑与
- 逻辑或
- 异或——A或者B(但不都满足)
- 相等——A和B相等
- 德·摩根律
- 卡诺图
- 包含未定义的逻辑
- 总结
- 余数 —— 周期性和分组
-
- 星期数的思考题
- 数学归纳法
- 我的总结与思考
-
- 噢!原来是这样啊……
前言
因为感觉数学不是太好,计算机方面又需要数学的知识,但是直接看数学的教材又看不太懂,加上也不想从事数学方面的工作,就看看《程序员的数学》来了解一下,它对于很多人可能是一本很基础的书籍,但对我来讲再合适不过。
这也是一本很有名的书籍,每个国家的书籍都会带有不同的特点,而日本书带给我最大的印象,就是通俗,好玩,甚至说是啰嗦,有的时候看日本人写的书籍,感觉翻来覆去那几个观点反复论证,生怕你听不懂了。
所以我相信这本书会让我有一些收获的,起码,我相信他想教给我的,我肯定能看懂。
我的章节安排也是按照书中的章节安排来做的,但是我并不平铺直叙的说书中的内容,而是说一些我的感受,或者总结书中的知识点,对于你而言,就是了解一下,如果你有和我一样的需求,或者你对此干兴趣的话,也推荐你去看这本书。 毕竟,这是我总结的,是我的东西,你看的是我总结的东西,肯定会味同嚼蜡,很枯燥,而书中是极其有趣的。

0的故事——无即是有
10进制计数法是我们平时使用的比较多的
- 使用的数字有0、1、2、3、4、5、6、7、8、9十个数字
- 数位从右往左分别表示个位、十位、百位、千位……
我们以2503这个数为例子。 2503表示的是以2、5、0、3这4个数字组成的一个称作2503的数。
只是因为数位不同而意义不同:
- 2表示“1000的个数”
- 5表示“100的个数”
- 0表示“10的个数”
- 3表示“1的个数”
那么2503就应该是2 * 1000 + 5 * 100 + 0 * 10 + 3 * 1 =2 * 103 + 5 * 102 + 0 * 101 + 3 * 100
= 2000 + 500 + 0 + 3
=2503
我们可以看到千位、百位、十位、个位分别可以称作103、102、101、100位,10进制计数法的数位全是10n的形式,这个10称作10进制计数法的基数或底。
基数的右上角的数字,我们称为指数,是从右向左为0、1、2、3这样有规律的顺次排列的。
2进制计数法是计算机在处理数据时所有的计数法
- 使用的数字只有,0、1,共2种,
- 从右往左分别表示1位、2位、4位、8位……
用2进制计数法来数数,首先是0,然后是1,接下来不是2,而是在1上面进位变成10,然后是11,100,101……
由10进制的原理相通:
以1100这个数字为例,各个数位也都有不同的意义,从左往右依次为:
- 1表示“8的个数”
- 1表示“4的个数”
- 0表示“2的个数”
- 0表示“1的个数”
也就是说2进制的1100是1个8、 1个4、 0个2、和0个1累加的结果,即8 + 4 + 0 + 0 = 12 。
所谓的8 4 2 1,就是23、 22、21、20。
2是2进制的基数或底。
基数转换
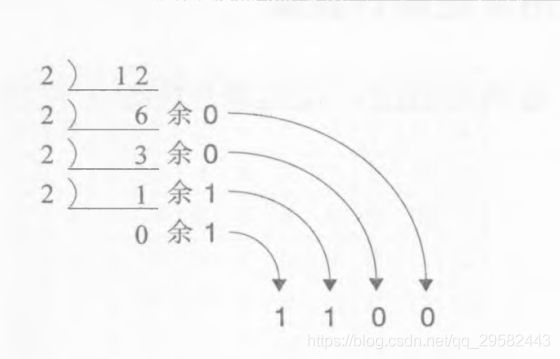
如果把10进制中的12转换为2进制,只需要将12反复地除以2(12除以2,商为6;6再除以2,商为3;3再除以2……),并写出余数是“1”还是“0”,余数为0则表示除完了,随后再将每步所得的余数逆向排列,由此就得到2进制表示了。
按位计数法
上面的10进制和2进制一般被称作按位计数法,除了十进制和2进制外还有很多种类的按位计数法,比如编程中也常常使用8进制和16进制计数法。
8进制计数法的特征如下:
- 使用的数字有0、1、2、3、4、5、6、7共8种数字
- 从右往左分别是80、81、82、83的位……(基数是8)
16进制计数法的特征如下:
- 使用的数字有0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F共16种
- 从右往左分别是160、161、162、163的位……(基数是16)
- 我们可以看到,在16进制计数法中,使用ABCDE(有时也用abcde)来表示10以上的数字
由此,我们可以推出
N进制计数法的特征如下:
1.使用的数字有0、1、2、3、……、N - 1,共N种
2. 从右往左分别是N0、N1、N2、N3的位……(基数是N)
不适用按位计数法的罗马数字
按位计数法在生活中最为常见,但实际上在我们身边也有不按位计数法的例子,比如**罗马计数法**,至今罗马数字还常常出现在钟表表盘上。
- 数位没有意义,只表示数字本身
- 没有0
- 使用I(1)、V(5)、X(10)、L(50)、C(100)、D(500)、M(1000)
表示3的话,就是III,也就是3个1叠在后面。
表示6的话,不是IIIIII,而是需要把IIIII表示为V,所以是VI。
表示61的话,就是LXI,表示为50 + 10 + 1 = 61。 实际上就是从左到右累加的结果
这就是罗马数字的加法,大的放左边,小的放右边,表示加法,把挨个表示的数字加起来
而罗马数字的减法,就是大的放右边,小的放左边,表示减法。VI表示5 + 1,IV则表示 5 - 1
比如:
- 200 + 10 -3 + 50 - 6怎么表示呢?
应该是CCLIIIIVX = CCLI
首先CCL代表100 + 100 + 50.
IIIIVX可以拆解为IIIIV和X
IIIIV是一个加法,加起来是1 + 1 + 1 + 1 + 5 = 9.
9在X(10)的左边,说明是减法,所以IIIV(9)X(10) = I(1)
所以答案是CCLI
指数法则
我记得刚开始学习指数的时候,接触的都是平方,后来能接触到一些立方,但诸如N0这种是在最后面学习的,记得书上只有一句话——任何数的0次方都等于1。
对当时的我而言,这句话只是几个字而已。。。就以10为基数演示,102是2个10相乘,100不应该是0个10相乘吗?怎么会是1呢?
那么为什么N0=1呢?还是拿10为基数演示:
我们可以看到,每当10的指数减1,数就变为原先的10分之1,因此,100就是1, 那么10n(n包括0)可以遵循下面的规律:
指数每减1,数字就变为原来的10分之1,那么我们也可以推出Nn的规律,指数每减1,数字就变为原来的N分之1.
那么我们保持住这个逻辑,再往下纵深,10-1是什么? 同样套用上面的规则(指数每减1,数字就变为原来的10分之1)
原来10-1 为1/10是非常理所应当的事情。

接下来我们再用相同的方法,推一下20的值,10n的时候,指数每减1,值就变为原来的1/10,很自然的想到,2n的时候,指数每减1,值就变为原来的1/2.
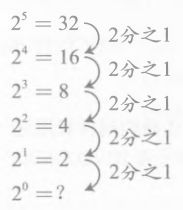
再往下纵深,2-1就是20的1/2,也就是20除以2。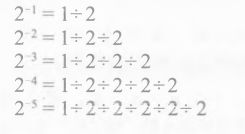
在从前的时候,我们记忆诸如100的值,是靠对公理的记忆,但是现在当我们重新捋出100的逻辑之后,我们让规则变得更简单了,我们在以后的学习中,更需要考虑的是,如何对一种现象进行适当的定义,以期让规则变得更简单。 这就从记忆力的问题转变为了想象力的问题,这种思维方式是这样的:“以简化规则为目标去定义值”。
到这里,之前的这些“规则”我们就取名为“指数法则”,接下来我们需要把这一部分的数学规则更抽象一些,就能得到指数法则的表达式了。
Na * Nb = Na+b
当我乍一看到这个表达式的时候,我还不太清楚它和前面的指数演变规律有什么联系,我们就看下面的演变,100是1,指数加1,相当于在原来的基础上乘10,那么:
101 = 1 * 10 = 100 * 101 = 100+1.
102 = 1 * 10 * 10 = 100 * 101 * 101 我们在上一个式子已经算得100 * 101 = 101
那么,100 * 101 * 101 = 101 * 101 = 101+1.
同理:
103 = 1 * 10 * 10 * 10 = 100 * 101 * 101 * 101 = 102 * 101 = 102+1.
这样,我们就证明了Na * Nb = Na+b.
在我当年,直接给我这样一个表达式的时候,我只是把它背了下来而已,但是这样层层的递进再去理解的时候,会发现指数法则的模型抽取原来是如此的合理。
0所起的作用
1、占位
例如用10进制表示2503,这里面的0表示十位“没有”,虽说“没有”,但是这个0不能省略,如果省略了,就变成了253,那就是另一个数字了,在按位计数法中,数位具有很重要的意义,0的作用就是占着一个位置以保证数位高于它的数字不会产生错位。
2、统一标准,简化规则
以2503举例,可以变成2 * 103 + 5 * 102 + 0 * 101 + 3 * 10 0 = 2503
如果没有规定N0 = 1. 我们就必须特别处理“1”这个数字,0在这里起到了标准化的作用。
人类的极限和构造的发现
数学表示法的历史
古埃及人: 使用5进制和10进制混合的计数法,不是按位计数法,不存在0,将数字记在一种纸莎草纸上。

巴比伦人: 在黏土板上用棱形记号来表示数,他们使用表示1和10的两种棱形记号来表示1~59,并通过记号所在的位置来表示60n的数位,由此10进账和60进账混合的按位计数法就诞生了,现在通用的1小时为60分钟,1分钟未60秒的时间换算就是源于巴比伦的60进制计数法。 另外因为黏土板和纸莎草纸有所不同,很难写多种白吐司的记号,因此,巴比伦人需要以尽可能少的记号来表示数,也许正因此,才促成了按位计数法的产生。
古希腊人: 不仅仅把数字当做运算工具,还在其中注入哲学真理。他们将图形、宇宙、音乐与数字相关联。
玛雅人: 数数时从0开始,使用的是20进制计数法。
罗马人: 使用5进制和10进制混用的罗马数字。将1、5、10、50、100、500、1000表示为I、V、X、L、C、D、M. 比如IV表示4,IX表示9. 将数字列在左侧表示减法的表示法是后来制定的,古罗马时并不这样用。
印度人: 印度人在引进巴比伦的按位计数法的时候,把“0”也引了进去,而且采用的是10进制计数法。现在我们使用的0~9,被称为阿拉伯数字而不是印度数字,也许是因为将印度数字传入西欧的是阿拉伯学者的缘故吧。
为了超越人类的极限
接下来为什么人类需要发明计数法呢?
以罗马数字为例,将5表示为V,不过好像将5表示为IIIII也可以,但是这种方法的弊端在于数越大就越难处理,比如IIIIIIIIII和IIIIIIIIIII哪个大?不能马上得知。而X和XI就能马上比较谁大谁小。
这就是前辈们创造出的“单元”的概念。假如要表示“十二”,比起IIIIIIIIIIII,用XII比较方便,若使用按位计数法,写成“12”则更方便。
10进制计数法和按位计数法都是因为人类的能力有限,所以面对大的数字必须简便的表示,而如今,我们的数据越来越大了,按位计数法也显得力不从心了,10000000000000和100000000000000哪个大呢?很难一眼看出来,这时候,指数表示法显得异常重要,如果把刚才的两个数字表示为1012 和 1013就可以一眼看出后者比较大。
其实,现代我们用计算机来解决人类难以处理的大规模问题,我们绞尽脑汁地思考如何在短时间内解决大规模问题,“要解决大问题,就将它分解为多个小“单元”,如果小“单元”还是很大,那就继续分解成更小的“单元”,直到问题最终解决”,这种方法至今通用,比如在编写大程序的时候,一般会分解成多个小程序(模块)来开发。
这就是问题分解法。
逻辑——真与假的二元世界
这个课前对话相当有意思,你细品。 前后两种相同的说法,回答却不一样。
逻辑的学习当然是至关重要的,特别是对于程序员而言,因为计算机是没有情绪的,它总是按照逻辑而执行。
很多人会觉得“逻辑冰冷且机械死板”。确实,逻辑有这种特征,但是正因如此,它才有用,人类太容易被各种事情所影响了,但计算机不同,计算机可以一直稳定的运行。
而程序员处于人类和计算机的分界线上,所以需要了解逻辑,当然,最好也要有另一边的温暖——虽然人极容易被影响,被驯化。
乘车费用问题——兼顾完整性和排他性
通过这个问题来学习逻辑的基本思路,并说明什么是完整性和排他性。

我们从这个表格的条件中,没有找到遗漏的地方,也没有重叠的地方。
为了接下来的说明更好理解,需要解释几个术语:
能够判断对错的陈述句叫做命题,下述语句都能判断对错,因此都是命题。
命题要么为true,要么为false,同时满足或者都不满足都不是命题。
Alice(13岁)的年龄在6岁以上。 —— 真(true)命题
Bob(4岁)的年龄在6岁以上。 —— 假(false)命题
有没有遗漏?
接下来我们重新审视规则A,我们发现不管任何一个年龄段的人来,我们都能判断“乘客的年龄在6岁以上”这个命题的真假。说明规则A没有遗漏。
再看规则C,会发现它判断了“乘客的年龄在6岁及以上”,以及“乘客的年龄在6岁及以下”的真假,如果乘客6岁,就满足了这两个规则,这当然是不合理的。

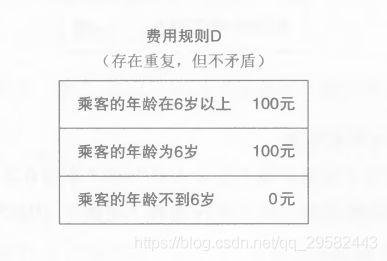
但是需要注意的是,只有当重复的部分互相矛盾时,规则才不符合逻辑
如下面的规则D,重复了,但不矛盾。
所谓“君子生非异也,善假于物也。” 人类最会善用各种工具而让自己的判断更加准确,让自己的压力变小,让自己的视角更清晰。 那么,有什么可以辅助我们思考这样的规则呢?
我们可以用数轴试试。
我们可能学过 “区间” 的概念,如下图:
假如说不包括6这一点,就要画一个空心圆,代表开区间。
假如说包括6这一点,就要画一个实心圆,代表闭区间。
那么我们可知“年龄不到6岁”的范围应该是0-6岁但不包含6岁(包含0岁),就应该是[0,6),左闭右开区间。
那么我们很容易就能看出来,下图是不具有“重复”和“遗漏的”。

规则B为什么会有“遗漏”呢?因为6岁那里左右两边的条件都没有“实心圆”,说明6岁没有考虑到逻辑中。
而再看C规则,有两个重叠的“实心圆”,说明左边的规则具备这个条件,右边的规则也具备这个条件,而他们的效果却是不一样的,这就是存在了重复问题,并且结果是冲突的。

我们可以看到,我们需要特别特别注意的是边界值。往往逻辑的错误,都是发生在边界上。
那么我们就可以来说“完整性”和“排他性”了:
没有“遗漏”,即具备完整性,由此证明该规则无论在什么情况下都适用。
没有“重复”,即具备排他性,由此明确该规则不存在矛盾的地方。
当我们遇到大问题的时候,通常将其分解为多个小问题。这个时候常用的方法就是检查它的**完整性和排他性。**即使是难以解决的大问题,也能通过这种方法转换为容易解决的小问题。
比如还是这个问题,我们可以用If语句分解
我们的大问题是“显示出乘客需要的费用”,分解成小问题就是“显示年龄在6岁以上的乘客的费用”和“显示年龄不到6岁的乘客的费用”
我们这就把一个大问题拆解成两个小问题了。 实际上,这种根据“命题的真假”来分解问题的方式,就是程序中常用的if语句
// Java
if(乘客的年龄在6岁以上){
显示"费用为100元"
} else {
显示"费用为0元"
}
我们可以看到,if语句的条件分支体现了“兼具完整性和排他性的分解”。
建立复杂命题
并不是所有的命题都纯粹而简单,有的时候为了表示出更为复杂的情形,需要建立复杂的命题。
比如 “乘客的年龄不到6岁,并且乘车日不是星期日。” 这个命题是由“乘客的年龄不到6岁”和“乘车日不是星期日”这两个命题组成的,这就是通过组合命题的方式,把命题复杂化。
逻辑非
接下来我们以 “乘车日是星期日” 这个命题为基础,可以建立“乘车日不是星期日”的命题,而这种“不是……”的命题的运算称作非,英语中用not表示。
假如这个命题为A,则A的逻辑非表达式写作:

那么A和非A可以表示为这样:

上图为真值表,因为A是明天,它要么是true,要么是false,因此,真值表覆盖了所有的情况,它也没有遗漏和重复,兼顾了完整性和排他性。
双重否定等于肯定
这个和我们的汉语一样,我在上初中的时候,语文老师经常强调 “双重否定表肯定” ,面对 “不得不” 这样的词就从容多了。
一个事物只有两种特性,当否定一次就变成另外一种,再否定一次就又变成了另外一种也就是相当于没有改变。

逻辑与
还是通过上面逻辑非的例子来讲,“年龄为6岁以上,并且乘车日是星期日” ,像“A并且B”这样的形式称作
A and B 就是 “仅当A和B都为true的时候,才为true” 的命题。
逻辑或
比如某超市持有礼卷A,或者礼卷B的顾客打折优惠,我们将这种“A或者B”的命题称作逻辑或,英语中用or表示。
异或——A或者B(但不都满足)
比如说“他现在在东京,或者他现在在大阪”,这个“或”和刚才讲的逻辑或有所不同,因为他只能在东京或大阪的其中一处,不可能同时身处两地。
这种就是异或。
相等——A和B相等
A = B
它和之前的蕴含表达式相同,可以这样解释——假设白色区域是陷阱,那么我们只要“不踏入A,或者待在B中”,就绝对不会落入陷阱了。

我们通过这个表达式的扩展可以知道原命题为真,不能说逆命题为真,但是可以说逆否命题为真。
A -> B 逆命题 B -> A 逆否命题 ┐B -> ┐A
德·摩根律
卡诺图
卡诺图是简化复杂逻辑表达式的有效工具。
现在有这样一个游戏——二灯游戏。
这个规则比较复杂,你能把它简化一下吗?

然后当我们按照之前学习的方式去组合逻辑的时候,会发现组合出来的逻辑是很复杂的。

这个时候,我们就不得不借助卡诺图了。
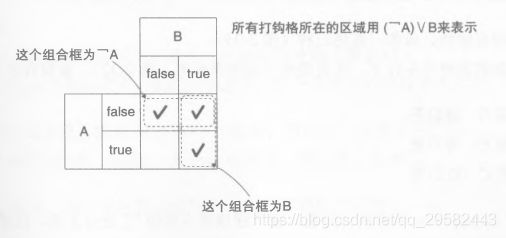
我们按照对应的规则,在框里面打勾。

接下来我们需要在这些打勾的格子里找到下面组合框中的最大组合框,组合框可以相互重叠。
比如说,我们就可以用两个1*2的组合框来组合起来。然后我们可以分析出来横着的组合框,就是A为false的区域,因此用┐A来表示。 再分析纵向的组合框,发现就是B为true的区域,因此用B来表示。
那么合到一起就是(┐A) V B。
那么我们在玩二灯游戏的时候,只需要观察当绿灯灭或黄灯亮的时候就可以按下按钮。
另外我们通过画卡诺图也可以知道上面两种方式是等价的。

包含未定义的逻辑
现在我们已经学习了逻辑的基本知识,逻辑上只用真(true)和假(false)两个真值进行运算。
但是在程序中,经常会由于发生错误,导致退出,崩溃,陷入死循环,抛出异常,得不到true和false中的任何一个值。
为了同样能表示这种“得不到值”的情况,在true和false的基础上,又新引入了一个叫underfined的值,为“未定义”。
总结
我们通过使用逻辑表达式,真值表,文氏图,卡诺图等工具,练习了如何解析复杂逻辑。
余数 —— 周期性和分组
奇数就是能被2除余1的整数,偶数就是能被2整除的整数,除法就像分组,根据余数来确定它属于哪个组。
这就是站在余数的角度进行思考。
星期数的思考题
如果今天今天是星期日,那么一百天以后是星期几?
第一种方法:
如果今天是星期日,一周有7天,那么7天后,14天后,21天后……这种“7的倍数”天后,都是星期日。
98是7的倍数,因此98天后也是星期日,那么99天后就是星期一,100天后就是星期二。
第二种方法:
我们也可以通过这种方法来表示一周的时间,假设今天是周日,100天以后的星期数就是“100除以7的余数”,100 / 7 = 14 余 2,因此是周二。

当我们想算1亿天以后是星期几的时候,通过第一种方式就比较难的能够算出来,但是通过用第二种方法可以很方便的算出来。
100000000 / 7 = 14285714 余 2
n天后的星期数,可以通过n除以7的余数来判断,因为星期数是以7位周期循环的,在面对庞大的数字的时候,只需要找到它的分组规律,就能用余数来解决它。
第三种方法:
如果我们想算10100 (即1后面跟100个0)天以后是星期几怎么办? 由于这个数字太大了,计算起来比较费力,即便借助计算器也很难完成。 我们的第二种方法是通过寻找一周日期的周期性来算出来的,那我们找找它还有没有其它规律呢?
我们不断的增加10的指数,发现它的余数以1,3,2,6,4,5不断的循环。
我们发现每增加6个0,星期数就相同,因此周期为6. 我们只需要将指数除以6,得到的余数为0,1,2,3,4,5的其中之一,就对应周一,周三,周二,周六,周四,周五。
100 / 6 = 16 余 4
因此10100天一会是周四

使用这种方法,就算是101亿天以后也能算出来:
100000000 / 6 = 16666666 余 4
余数为4,答案为星期四,由此可见,在处理难以计算的超大数字时,发现与之相关的规律相当重要。
数学归纳法
我的总结与思考
噢!原来是这样啊……
我数学不好的本质是什么呢?可能是因为我的数学底子太差,我的数学大厦搭建的歪七扭八,很多基本的概念都理不清楚,说不明白,也不知所以然,对我而言,很多的公理,真的只是一些文字的堆积而已,我从未在老师讲过之后,去探索一下人类探寻这些如此直白的简单的公理花费了多少精力,又有多少故事在其中,这一定是很有趣的,书上的那些数学大拿们,在我的脑中也不会如此的没有生机了。
而本书在开篇就给我带来了这样一种感觉——“当我看到讲指数的时候,我心里想,讲的也太基础了吧,这谁不会啊,但是就是这样一个我们再熟悉不过的概念,当我读过之后,我也仍感觉:噢!原来是这样啊……”。 它会让我一次又一次的感觉,原来我从前对这个这么直白的概念的了解始终差一层,这样很多个直白的概念,差了一层之后,偏差之千里了,数学怎么能学好呢?
祝秋安
未完待续。。。