Panoptic Segmentation(全景分割)论文阅读笔记与源代码分析
【Panoptic Segmentation论文下载地址】
【github代码实现】
目录
- 1. 摘要与介绍
-
- 要点
- things和stuff的区别:
- 论文所叙述的全景分割任务的大致思想:
- 2. 相关工作
-
- 多任务网络和单任务网络的区别
- 3. Panoptic Segmentation Format
-
- task format
- Stuff 和 thing 标签
- 与语义分割的关系
- 与实例分割的关系
- 4. 全景分割度量指标:panoptic quality (PQ)
-
- Segment Matching
- PQ computation
-
- PQ公式解释:
- Void Labels
- Group Labels
- 5. Machine Performance Baselines
1. 摘要与介绍
要点
- 提出了一个概念“全景分割”(Panoptic Segmentation,PS),全景分割统一了两个经典的任务:语义分割(semantic segmentation,为每一个像素点分配类别标签)、实例分割(instance segmentation,检测并分割每一个对象实例)。
- 全景分割的目标:生成丰富且完整的连贯场景分割。
- 提出了一种新的度量panoptic quality(PQ),它以可解释和统一的方式捕获所有类(stuff and things)的性能。
things和stuff的区别:
things: 可数的物体,比如人、物体等。—实例分割解决。使用锚框或者掩码来描绘物体。
stuff: 类似纹理或材料的无定形区域,如草、天空、道路。—语义分割解决。这个任务被简单地定义为为图像中的每个像素分配一个类标签(注意,语义分割将类视为stuff)。
从上面的叙述中也容易看出来实例分割和语义分割的区别,全景分割是一个更统一的、更全局的看法。那么对于语义分割、实例分割、全景分割三种任务的效果,使用论文中的图来展示如下:
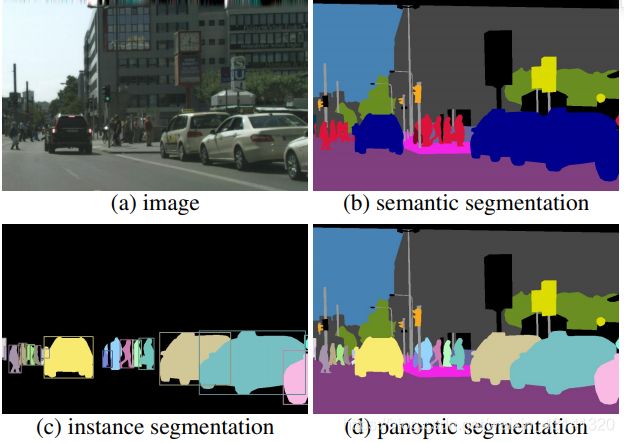
那么从这张图中就能够更好的体现全景分割的任务:
- 同时包含thing类别和stuff类别。
- 使用简答但是通用的格式。
- 对于所有的类别提出一种通用的评估度量指标。
论文所叙述的全景分割任务的大致思想:
- 图像中的每一个像素点都要分配一个语义标签或者一个实例ID。
- 拥有相同的label和ID的像素点属于相同的物体;对于stuff标签,实例ID就会被忽略。
- 使用启发式方法,它通过一系列合并输出的后处理步骤,将两个独立系统的输出结合起来进行语义和实例分割。
2. 相关工作
多任务网络和单任务网络的区别
多任务网络允许独立和潜在不一致的东西输出,而单任务(PS)需要一个单一的连贯的场景分割。
3. Panoptic Segmentation Format
task format
给定预先确定的编码了L个语义类别的集合 L : = { 0 , … , L − 1 } \mathcal{L}:=\{0, \ldots, L-1\} L:={ 0,…,L−1},任务需要设计全景分割算法,将图像中的每一个像素点匹配为 ( l i , z i ) ∈ L × N \left(l_{i}, z_{i}\right) \in \mathcal{L} \times \mathbb{N} (li,zi)∈L×N的pair格式,其中 l i l_{i} li表示像素i的语义类别, z i z_{i} zi表示像素i的实例id。Ground truth注释以相同的方式编码。无法确定的像素点以及现有类 L \mathcal{L} L以外的像素点可以被指定一个特殊的空标签(None);也就是说,不是所有的像素都必须有一个语义标签。
Stuff 和 thing 标签
语义标签由 L S t \mathcal{L}^{\mathrm{St}} LSt 和 L T h \mathcal{L}^{\mathrm{Th}} LTh组成,二者满足: L = L S t ∪ L T h \mathcal{L}=\mathcal{L}^{\mathrm{St}} \cup \mathcal{L}^{\mathrm{Th}} L=LSt∪LTh且 L S t ∩ L T h = ∅ \mathcal{L}^{\mathrm{St}} \cap \mathcal{L}^{\mathrm{Th}}=\emptyset LSt∩LTh=∅。两个子集合分别对应的是stuff标签和thing标签。
读到这里觉得有点奇怪,既然是语义类别标签为什么还包thing标签,可能还是读到这里还没体会到论文所描述的“联合任务(joint task)”的实质。
当一个像素点的 l i ∈ L S t l_{i} \in \mathcal{L}^{\mathrm{St}} li∈LSt的时候,那么该像素点所对应的实例id就无关紧要了,也就是说,拥有相同的语义类别(None除外)的像素点,他们就同属于一个类;否则,当 l i ∈ L T h l_{i} \in \mathcal{L}^{\mathrm{Th}} li∈LTh的时候,所有拥有相同的 ( l i , z i ) \left(l_{i}, z_{i}\right) (li,zi)的像素点同属相同的instance,比如车。所以相应的,同属于一个instance 类别的像素点一定拥有相同的 ( l i , z i ) \left(l_{i}, z_{i}\right) (li,zi)。读到这里,可以体会到 l i l_{i} li可以起到判断当前的像素是instance还是stuff的作用,哪些类别是stuff哪些类别是thing也只是程序员自己的设定罢了(设计 L \mathcal{L} L集合)。
与语义分割的关系
- 全景分割和语义分割两个任务都要求给图像中的每个像素分配一个语义标签。
- 如果ground truth没有指定实例类别,或者所有类都是stuff,那么任务格式是相同的(尽管任务度量不同)。
- 全景分割包含了thing类别(每个图像可能有多个实例),这个就使得两种任务有了不同。
与实例分割的关系
实例分割允许重叠片段,而全景分割任务只允许为每个像素分配一个语义标签和一个实例id,对于全景分割不可能有重叠,这一特点在后面介绍的性能评估上有重要的作用。
4. 全景分割度量指标:panoptic quality (PQ)
不同于前人提出的单一任务语义分割或者实例分割的独立的评估指标,论文提出的统一的评估指标适用于二者的联合任务。该评估指标需要同时考虑到这几个方面:
- 完整性:
度量指标应该以统一的方式处理thing和stuff类,关注任务的所有方面。 - 可解释性:
可以促进沟通和理解。 - 简洁性:
容易被定义和实现。
PQ的大体步骤:
- Segment Matching
- PQ Computation
Segment Matching
定理:给定一个预测结果和groud truth,对于groud truth中的每一块分割的掩码来说,在预测的结果中至多有一块预测掩码与其IOU大于0.5,反之亦然。
证明:设 g g g是groud truth 中的一块分割掩码, p 1 p_{1} p1和 p 2 p_{2} p2分别是预测结果中的两个分割掩码。通过一开始假设预测的掩码部分互不重叠,所以有: p 1 ∩ p 2 = ∅ p_{1} \cap p_{2}=\emptyset p1∩p2=∅,又因为: ∣ p i ∪ g ∣ ≥ ∣ g ∣ \left|p_{i} \cup g\right| \geq|g| ∣pi∪g∣≥∣g∣,所以我们可以得到:
IoU ( p i , g ) = ∣ p i ∩ g ∣ ∣ p i ∪ g ∣ ≤ ∣ p i ∩ g ∣ ∣ g ∣ for i ∈ { 1 , 2 } \operatorname{IoU}\left(p_{i}, g\right)=\frac{\left|p_{i} \cap g\right|}{\left|p_{i} \cup g\right|} \leq \frac{\left|p_{i} \cap g\right|}{|g|} \quad \text { for } i \in\{1,2\} IoU(pi,g)=∣pi∪g∣∣pi∩g∣≤∣g∣∣pi∩g∣ for i∈{ 1,2}
对i求和,因为 ∣ p 1 ∩ g ∣ + ∣ p 2 ∩ g ∣ ≤ ∣ g ∣ \left|p_{1} \cap g\right|+\left|p_{2} \cap g\right| \leq|g| ∣p1∩g∣+∣p2∩g∣≤∣g∣以及 p 1 ∩ p 2 = ∅ p_{1} \cap p_{2}=\emptyset p1∩p2=∅,所以我们可以得到:
IoU ( p 1 , g ) + IoU ( p 2 , g ) ≤ ∣ p 1 ∩ g ∣ + ∣ p 2 ∩ g ∣ ∣ g ∣ ≤ 1 \operatorname{IoU}\left(p_{1}, g\right)+\operatorname{IoU}\left(p_{2}, g\right) \leq \frac{\left|p_{1} \cap g\right|+\left|p_{2} \cap g\right|}{|g|} \leq 1 IoU(p1,g)+IoU(p2,g)≤∣g∣∣p1∩g∣+∣p2∩g∣≤1
因此,如果说 IoU ( p 1 , g ) > 0.5 \operatorname{IoU}\left(p_{1}, g\right)>0.5 IoU(p1,g)>0.5,那么一定有: IoU ( p 2 , g ) < 0.5 \operatorname{IoU}\left(p_{2}, g\right)<0.5 IoU(p2,g)<0.5;交换p1和p2的这一假设条件可以得到结论:只有一个预测掩码部分与ground truth的掩码部分的IoU严格大于0.5。
有一个疑问:为什么这里IOU一定要设置0.5为阈值呢?因为对于较小的IOU,将需要其他匹配技术,但是在实验中表明,较低的阈值是不必要的,因为IOU≤0.5在实践中是罕见的。
PQ computation
独立计算每个类的PQ,并对所有类进行平均,因为这样可以防止PQ对于类别不平衡过于敏感。对于每一个类别,唯一的匹配将预测结果和groud truth分为三个集合(为了体现论文的原表述,这里直接用英文列出来):
true positives (TP):matched pairs of segments。
false positives (FP):unmatched predicted segments。
false negatives (FN ):unmatched ground truth segments。
如果还没有理解三者的定义,可以借助论文中的这张图来理解:

根据上面提到的,这样来定义PQ:
P Q = ∑ ( p , g ) ∈ T P IoU ( p , g ) ∣ T P ∣ + 1 2 ∣ F P ∣ + 1 2 ∣ F N ∣ \mathrm{PQ}=\frac{\sum_{(p, g) \in T P} \operatorname{IoU}(p, g)}{|T P|+\frac{1}{2}|F P|+\frac{1}{2}|F N|} PQ=∣TP∣+21∣FP∣+21∣FN∣∑(p,g)∈TPIoU(p,g)
PQ公式解释:
分子部分: 1 ∣ T P ∣ ∑ ( p , g ) ∈ T P IoU ( p , g ) \frac{1}{|T P|} \sum_{(p, g) \in T P} \operatorname{IoU}(p, g) ∣TP∣1∑(p,g)∈TPIoU(p,g)是matched segments的平均IOU,分母中 1 2 ∣ F P ∣ + 1 2 ∣ F N ∣ \frac{1}{2}|F P|+\frac{1}{2}|F N| 21∣FP∣+21∣FN∣用于惩罚未匹配的segments。这里认为所有segment的重要性是相等的,不管它们的区域在哪。
进一步的,如果我们分别乘和除TP集合的大小,那么PQ就可以视作segmentation quality (SQ)和recognition quality (RQ)的乘积:
P Q = ∑ ( p , g ) ∈ T P IoU ( p , g ) ∣ T P ∣ ⏟ segmentation quality (SQ) × ∣ T P ∣ ∣ T P ∣ + 1 2 ∣ F P ∣ + 1 2 ∣ F N ∣ ⏟ recognition quality (RQ) \mathrm{PQ}=\underbrace{\frac{\sum_{(p, g) \in T P} \operatorname{IoU}(p, g)}{|T P|}}_{\text {segmentation quality (SQ) }} \times \underbrace{\frac{|T P|}{|T P|+\frac{1}{2}|F P|+\frac{1}{2}|F N|}}_{\text {recognition quality (RQ) }} PQ=segmentation quality (SQ) ∣TP∣∑(p,g)∈TPIoU(p,g)×recognition quality (RQ) ∣TP∣+21∣FP∣+21∣FN∣∣TP∣
以这种方式书写,RQ与广泛使用的目标检测的度量指标F1非常相似。SQ只是matched segments的IOU的平均值。二者并不是独立的,因为SQ只是matched segments上的度量标准。
Void Labels
在groud truth中,有两种情况造成空标签:已有的类别之外的像素、模糊或者未知的像素,由于通常无法区分这两种情况,所以我们不评估空标签像素的预测,具体处理如下:
- 移除预测segment内部的空标签像素点,且不影响IOU的计算。
- 匹配完成之后,对于不匹配的预测segments,如果包含了一部分空像素且超过匹配阈值,那么将被删除,而且不会计算为false positives。
- 最终输出可能不会包含空像素点,而且不会影响评估。
Group Labels
在难以准确描述每个实例的情况下,使用Group Labels代替相同语义类的相邻实例的实例id。对于PQ的计算具体如下:
- 在匹配阶段,不使用group regions。
- 匹配完成之后,对于不匹配的预测segments,如果包含了一部分同一组中同类像素点且超过了匹配阈值,那么将被删除,并且不算作假阳性。