差分约束系统

在一个差分约束系统(system of difference constraints)中，线性规划矩阵A的每一行包含一个1和一个-1，A的其他所有元素都为0。因此，由Ax≤b给出的约束条件是m个差分约束集合，其中包含n个未知量，对应的线性规划矩阵A为m行n列。每个约束条件为如下形式的简单线性不等式：xj-xi≤bk。其中1≤i,j≤n，1≤k≤m。

例如，考虑这样一个问题，寻找一个5维向量x=(xi)以满足：

 

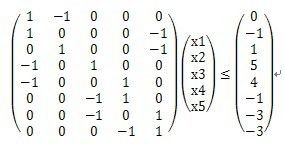
这一问题等价于找出未知量xi，i=1,2,…,5，满足下列8个差分约束条件：

x1-x2≤0

x1-x5≤-1

x2-x5≤1

x3-x1≤5

x4-x1≤4

x4-x3≤-1

x5-x3≤-3

x5-x4≤-3

    该问题的一个解为x=(-5,-3,0,-1,-4)，另一个解y=(0,2,5,4,1)，这2个解是有联系的：y中的每个元素比x中相应的元素大5。

 
引理：设x=(x1,x2,…,xn)是差分约束系统Ax≤b的一个解，d为任意常数。则x+d=(x1+d,x2+d,…,xn+d)也是该系统Ax≤b的一个解。

 

约束图

   在一个差分约束系统Ax≤b中，m X n的线性规划矩阵A可被看做是n顶点，m条边的图的关联矩阵。对于i=1,2,…,n，图中的每一个顶点vi对应着n个未知量的一个xi。图中的每个有向边对应着关于两个未知量的m个不等式中的一个。

   给定一个差分约束系统Ax≤b，相应的约束图是一个带权有向图G=(V,E)，其中V={v0,v1,…,vn}，而且E={ (vi,vj) : xj-xi≤bk是一个约束}∪{ (v0,v1) , (v0,v2) , … , (v0,vn) }。引入附加顶点v0是为了保证其他每个顶点均从v0可达。因此，顶点集合V由对应于每个未知量xi的顶点vi和附加的顶点v0组成。边的集合E由对应于每个差分约束条件的边与对应于每个未知量xi的边(v0,vi)构成。如果xj-xi≤bk是一个差分约束，则边(vi,vj)的权w(vi,vj)=bk（注意i和j不能颠倒），从v0出发的每条边的权值均为0。

  
定理：给定一差分约束系统Ax≤b，设G=(V,E)为其相应的约束图。如果G不包含负权回路，那么x=( d(v0,v1) , d(v0,v2) , … , d(v0,vn) )是此系统的一可行解，其中d(v0,vi)是约束图中v0到vi的最短路径(i=1,2,…,n)。如果G包含负权回路，那么此系统不存在可行解。

 

差分约束问题的求解

   由上述定理可知，可以采用Bellman-Ford算法对差分约束问题求解。因为在约束图中，从源点v0到其他所有顶点间均存在边，因此约束图中任何负权回路均从v0可达。如果Bellman-Ford算法返回TRUE，则最短路径权给出了此系统的一个可行解；如果返回FALSE，则差分约束系统无可行解。

   关于n个未知量m个约束条件的一个差分约束系统产生出一个具有n+1个顶点和n+m条边的约束图。因此采用Bellman-Ford算法，可以再O((n+1)(n+m))=O(n^2+nm)时间内将系统解决。此外，可以用SPFA算法进行优化，复杂度为O(km)，其中k 为常数。