G.Jerry的最速下降法笔记

该笔记初衷为期末复习所用，引用出处均已注明，涉及个人理解部分如果有不对之处，还请批评指正，俺会虚心接受滴！

1. 应用范围

无约束优化问题。

2. 相关定义(因为俺的基础比较差所以多给出一些定义，引用于https://www.zhihu.com/question/36301367/answer/156102040)

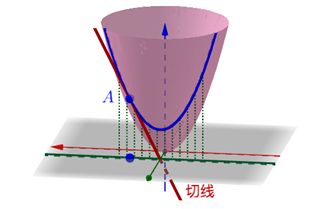
定义1  偏导数：如图1所示，在xy平面中，存在平行于x轴(或y轴)的绿色直线和与其共面的蓝色曲线，关于这条曲线的红色切线的斜率。

 

图1

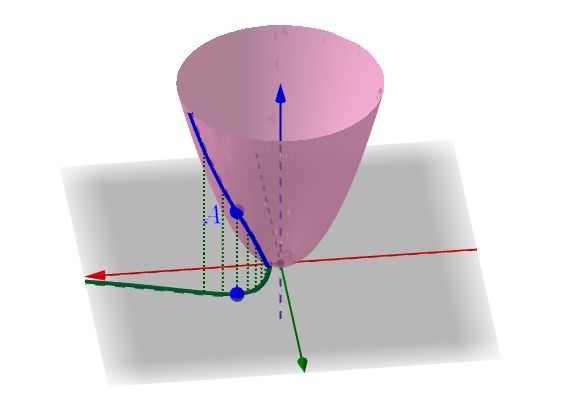
定义2  方向导数：，其意义为：f(x)在点x(k)处，沿方向d的变化率。即图2中红色直线的斜率。

注：在二维坐标系中，过某一点的切线只有一条；在三维坐标系中，过某一点的切线有很多条，它们可以组成一个切平面。因此，对于三维图像中的某一点，只有先确定一个方向d(方向向量)，才能找到与d重合或共面的唯一切线，其斜率记为f(x)沿d方向的导数。

已知直线可以向两个方向无限延伸，那么沿一个方向取得方向导数的最大值，沿反方向取得方向导数的最小值。

图2

梯度是一个矢量，它的方向是方向导数中取到最大值的方向，它的大小是方向导数的最大值。

那么，方向导数在什么方向最大？在图4中，方向导数最大<=>梯度方向<=>↙最陡峭↗(该句看不懂请忽略)。以小和尚下山为例，沿最陡峭的路线走时，小和尚下得最快。因此，沿着梯度方向函数值增长最快，沿着负梯度方向函数值减少最快。

定义3  全导数：通过图3来简单体会一下。(本节用不上)

图3

那么，它们的数值如何计算呢？百度说这么算！

 3. 原理

        举个栗子！此刻，Jerry和Tom在山顶，分别想去往山谷的两个最低处看湖。可是它们戴的头灯只能照亮一步远，只好摸索着向下走。这时，Jerry灵光乍现想起“最速下降法”！于是它每次沿着一个方向向下走一步；根据陡峭长度不同，Jerry每步的长度也不同，大约按照图中路线可以最快抵达。显然，它的路线可以用行进的方向和步长来阐述。

图4(介个图也是前方参考的大聪明作者画的！)

        猜猜Jerry到底走的是哪个方向？设f(x)连续可微，函数值递减<=>方向导数为负。方向导数最小的方向<=>↖梯度↘反方向=坡度最陡=函数值下降最快。因此，f(x)在点x(k)处的搜索方向满足：方向导数最小。

       猜猜Jerry每走了多长？记当前落脚点与下一步落脚点 之间的距离为步长λ，记下一步落脚点为，即的极小点。此时，Jerry沿着最陡峭的方向一步下落至它所能及的最低处。于是，当时取得极小点，这就可以求出Jerry的步长。同时，

又表明 和存在正交关系。

3.步骤

        总之呢就是，先找到一个初始点，每个点按照规定的步长和方向去延伸，当精度要求满足时停下！这里附上俺们教材上的步骤。

2021.09.24