matlab FFT函数解析 画频谱为什么要/N*2

一、问题

在用matlab FFT函数计算频谱时经常看到如下说法：

matlab fft文档 有如下代码画频谱：

clear;close all
Fs = 1000;            % 采样频率                    
T = 1/Fs;             % 采样周期       
L = 1500;             % 截取的信号长度
t = (0:L-1)*T;        % 时间矢量
%构造一个信号，其中包含幅值为 0.7 的 50 Hz 正弦量和幅值为 1 的 120 Hz 正弦量
X = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);
%在时域中绘制原始信号
subplot(2,1,1),plot(1000*t(1:100),X(1:100))
title('部分原始信号X(t)')
xlabel('t (milliseconds)')
ylabel('X(t)')
%计算信号的傅里叶变换
Y = fft(X); 
%计算双侧频谱 P2。然后基于 P2 和偶数信号长度 L 计算单侧频谱 P1。
P2 = abs(Y/L); 
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
%定义频域 f 并绘制单侧幅值频谱 P1。与预期相符，频率和幅值与理论相同
f = Fs*(0:(L/2))/L;
subplot(2,1,2),plot(f,P1) 
title('X(t)的单边幅值谱')
xlabel('f (Hz)')
ylabel('|P1(f)|')

那么为什么要有/N*2呢？

P2 = abs(Y/L); 
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);

二、定义

先要搞懂FFT在算什么，以及画的频谱是什么。
1、matlab 的FFT完全按照DFT方式运行的。
2、实际画是频谱（而不是频谱密度，不引起混淆时也简称频谱）。通俗来说，是傅里叶级数（而不是傅里叶变换）：
参考文献



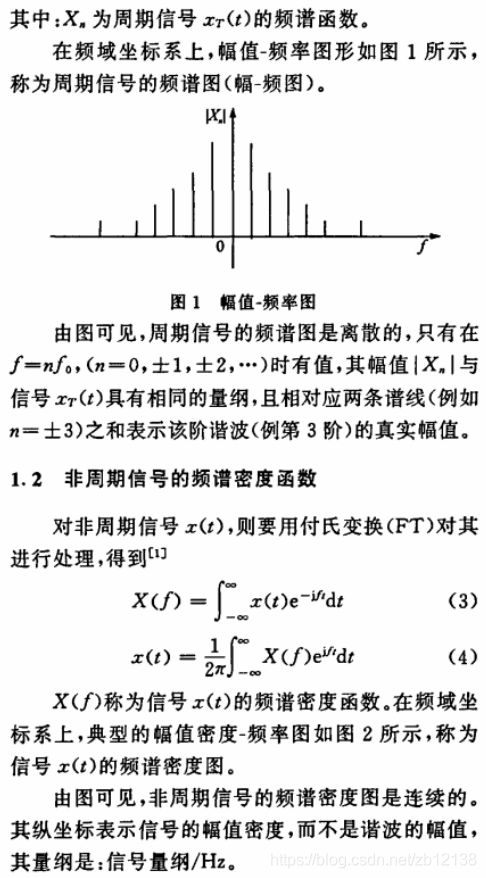
即画的频谱是傅里叶级数ak（若是单边谱，则是2ak）。

三、FFT和频谱的关系

简单解释：

1、由采样定理，频域可观察范围 -fs/2~fs/2，横轴变换奇偶略微不同：

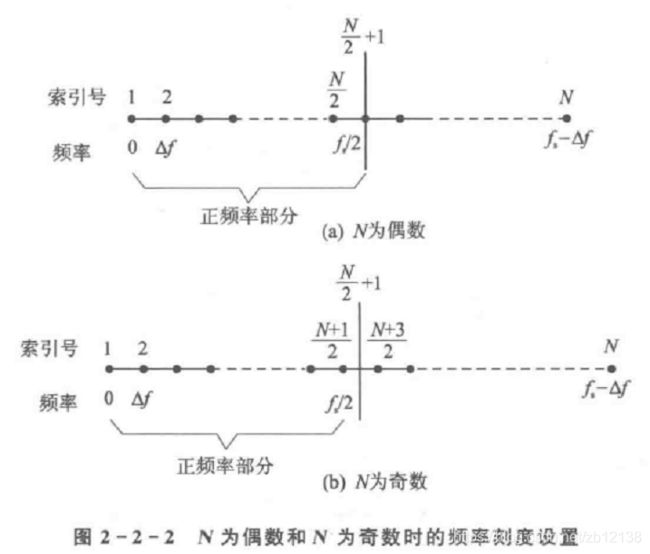
code:（以偶数N为例）

f = linespcae(0,Fs/2, N/2 + 1);      %单边谱 
f = linespcae(0,Fs - Fs/N, N) -Fs/2; %双边谱 

2、幅值上：

也就是说对于双边谱，要计算傅里叶级数|f|≤fs/2，FFT需要先shift，再/N（频谱），计算傅里叶变换需要/Fs（频谱密度）相关code如下：

% demo1
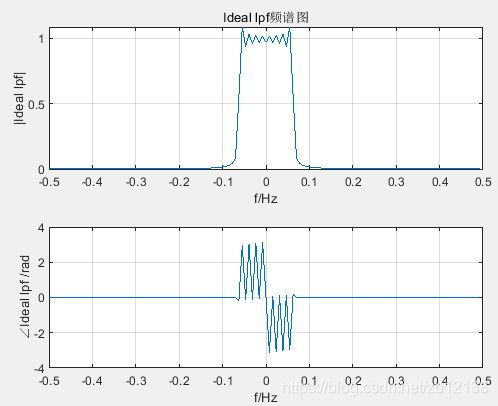
% 画低通滤波器频谱密度：
% Fs_ = 1;
% fc = Fs_/16; %归一化的截止频率，实际截止频率=fc/fs(滤波器)*fs(信号)
% LPF =@(t)2*fc*sinc(2*fc*(t)); %sinc = sin(pi*t)/(pi*t)
% L_ = 128;
% t0 = L_/2/Fs_;
% t_ = linspace(-t0,t0,L_);
% lpf_o = LPF(t_);
% figure
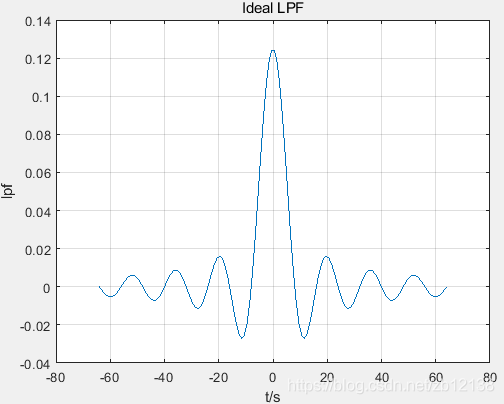
% plot(t_,lpf_o);title('Ideal LPF') ;grid on;
% xlabel('t/s'),ylabel('lpf');
% fftfun(lpf_o,Fs_,'Ideal lpf')

% % demo2
% % 画0.7*sin(2*pi*50*t) + sin(2*pi*120*t)的频谱：
SIN=@(t)0.7*sin(2*pi*50*t) + sin(2*pi*120*t);
w0 = 2*pi*10;
Fs = 4*w0; %必须是整数倍,否则sin_o 不是周期的
t = (1:2048)/Fs;
sin_o = SIN(t);
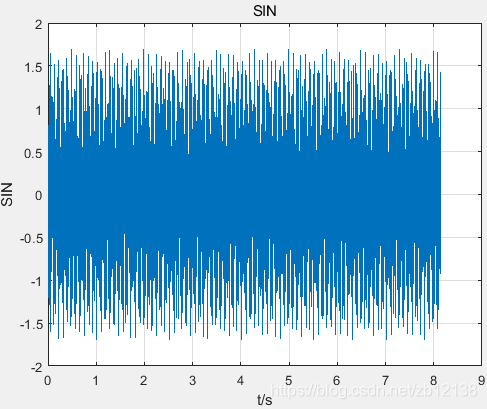
figure
plot(t,sin_o);title('SIN') ;grid on;
xlabel('t/s'),ylabel('SIN');
fftfun(sin_o,Fs,'SIN',true)

function fftfun(y1,Fs,name,isFs,a,b)  
    % 画频谱（密度）的函数，isFs指定是否是频谱,a,b指定频率显示范围
    N=length(y1);
    if nargin == 3
        isFs = false;
    end
    Cos = Fs;
    if (isFs)
       Cos = N;
    end
    y1fft=fftshift(fft(y1,N));
    f = linspace(0,Fs-Fs/N,N) - Fs/2;
    figure
    subplot(2,1,1)
    plot(f,abs(y1fft)/Cos);
    title(strcat(name,'频谱图')) ;grid on;
    xlabel('f/Hz'),ylabel(sprintf('|%s|',name));

    if nargin == 6
        xlim([a,b])
    end
    theta = angle(y1fft);
    theta(abs(y1fft)< max(abs(y1fft))/10) = 0;
    subplot(2,1,2)
    plot(f,theta) ;
    
    grid on;
    xlabel('f/Hz'),ylabel(sprintf('∠%s /rad',name));
    if nargin == 6
        xlim([a,b])
    end
end

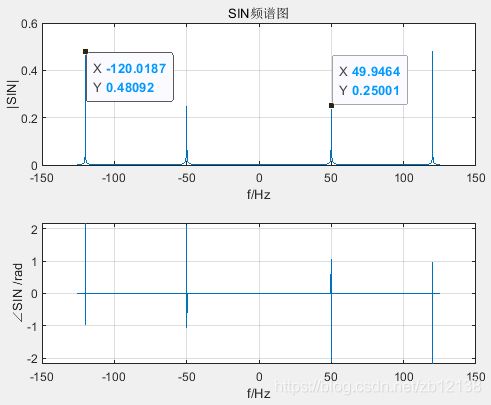
为什么要*2：
实信号的频谱是实部实对称的，双边谱把负频率幅值加到正频率即可。

复杂解释：

1、就是研究DFT和ak的关系
2、研究思路：FFT=DFT->DTFT->CTFT->ak

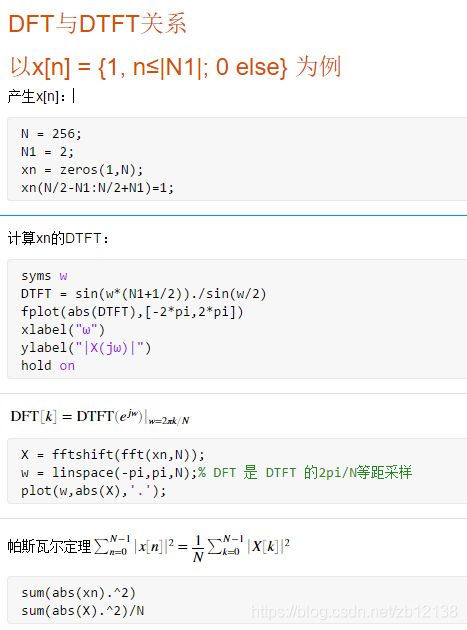
1、DFT是DTFT的一个周期的2pi/N等距采样

ref 《数字信号处理一一基于计算机的方法( 第四版)》p146

即：

在主周期内，DFT是DTFT的一个周期的2pi/N等距采样：

这个主周期在0~N-1对应的范围是[0,pi)，但DFT经过fftshift后就是[-pi,pi）这也是为什么要频率搬移。

实验检验：

输出：

2、DTFT是CTFT的采样平移叠加

ref 《信号与系统》p386



这和前面推导的结果一样。